I developed an OpenMP parallel program that determines whether two graphs are isomorphic. The goal is to have speedup scale as well as possible with an increasing number of processors. In graph theory, a graph is a set of vertices interconnected by a set of edges. Two graphs are isomorphic if they are a bijection between their respective vertex sets. Bijection between graph A and B means that each vertex in graph A can be assigned to each vertex in graph B, such that the edge structure is preserved. Note that a bijection can also be a permutation if the vertices of A and B have exactly the same names. The graph isomorphism problem is well-studied in computer science. Graph isomorphism is used to identify chemical compounds in a database, verify integrated circuit layouts against circuit schematics, perform zero-knowledge proofs in information security, and etc.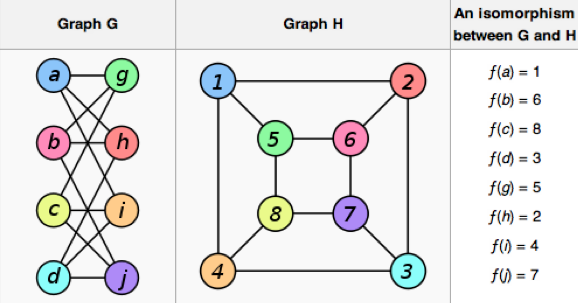

Source: wikipedia

It has been determined to be a NP problem, but is not known whether it's NP-complete. The most cited, and widely-used algorithm to solve graph (and subgraph) isomorphism is J. R.Ullmann's algorithm, which has O(N^3) average and O(N!) worst-case complexity, N being the number of vertices. This is the basis for the algorithm I have implemented.

Given two input adjacency matrices (which I randomly generated from another program I wrote), this program must determine if the graphs they represent are isomorphic. To prove that they are isomorphic, the program finds and outputs a valid permutation matrix P that can be applied as follows:


If it is determined that such a permutation matrix does not exist, then the graphs are not isomorphic.

Assumptions:
Two adjacency matrices are given as input, which represent simple graphs. Simple graphs are defined as graphs with the following properties:
No loops (edges from a vertex to itself). No disconnected subgraphs (a path exists between each vertex, but not necessarily an edge).
No parallel edges (at most one edge between two vertices).
Adjacency matrices are defined as matrices that disregard the lengths of each edge, rather only captures the existence of an edge between vertices.

Data Structures:
int P[MAX_N][MAX_N]; //permutation matrix P
int newP[MAX_N][MAX_N]; //scratch space to perform updates to P
int adjA[MAX_N][MAX_N], adjB[MAX_N][MAX_N]; //Adjacency matrices A and B
int degA[MAX_N], degB[MAX_N]; //degrees arrays degA and degB
int sortedDegA[MAX_N], sortedDegB[MAX_N]; //sorted degree arrays sortedDegA and sortedDegB
int distA[MAX_N][MAX_N], distB[MAX_N][MAX_N]; //all-pair shortest distance matrices distA and distB
int newDistA[MAX_N][MAX_N], newDistB[MAX_N][MAX_N]; //scratch space to perform updates to distA and distB

Memory usage is O(N^2) My algorithmic approach is specifically referenced from another student project report from the ECE department at Rice University. My job was to implement their (sequential) algorithm from scratch and then parallelize it. The algorithm is deterministic (as in it will always find the right answer and be consistent per run). The algorithm consists of two main phases: what I would call the preprocessing phase, and the brute force phase. The premise of the algorithm is to achieve polynomial run time by offloading as much work as possible from phase 2 (high complexity brute force search) to phase 1 (series of simpler and faster sub-algorithms). The computational part of the program is described as follows:

Parallel Compare Vertex Degrees
The first step is to compute the degree of each vertex and write them to a size-N array. This is essentially a parallel reduce function, hence the adjacency matrix can be decomposed by rows, and the edge counting can be performed in data-parallel fashion. However decomposition by rows limits the maximum parallelism (maximum number of useful threads) to N. The degrees of both input graphs need to be recorded, so a total of two size-N arrays of integers are allocated in this stage.

Parallel Merge Sort the Degree Arrays The degrees arrays must be sorted before they can be compared. I chose to implement a merge sort because it was intuitive to parallelize due to its 'divide-and-conquer' nature. Basically, I used the OpenMP task system to dynamically assign threads to different segments of the degrees array, and sort them in place. After each iteration of the sort, the threads must synchronize. The maximum parallelism in merge sort, starting with N/2 in the first sorting iteration, cuts in half after each iteration, since the number of elements to be sorted by a single thread doubles after each iteration.

Compare sorted degree matrices
At this point, the sorted degree arrays are compared (the only code left to run sequentially because it such a trivial operation, although this may have been a mistake.. per the effect of Amdahl's Law as explained in the results section). If the degree arrays are different, the program can immediately stop and declare the graphs non-isomorphic.

Parallel Degree Filtering
The premise for this stage is that vertices must be mapped to vertices with the same degree. Each element in the permutation matrix represents a possible mapping between vertex i and vertex j. So, decompose the permutation matrix P by rows. For each element in the row, compare the degree of vertex i to that of vertex j. If not equal, 0 that element in P. This stage is highly data-parallel. The single possible parallelism issue is false sharing (since processors are assigned to rows in an interleaved fashion), however the chance of false sharing is insignificant for N >> 16 (because 16 integers fit in a cache line for the architecture of Blacklight). Such is true because I chose the sufficiently-challenging 1000-vertex case to be my metric.

Parallel Check for Impossibility or Certainty of isomorphism
Decompose by rows and have each thread count the number of 1s in the row. If all rows have contain only one 1, then the isomorphism has been found. If any thread discovers a row of all zeroes, immediately have the program return 'non-isomorphic'.

Computing all-pair shortest distance matrices with Floyd-Warshall algorithm
This stage computes the shortest distance between vertices (the fewest number of edges in a path connecting two vertices). The shortest distance matrices will be used in the next stage to perform 'distance filtering'. The shortest distance matrices are computed via the Floyd-Warshall algorithm.[reference 3] This algorithm first initializes the shortest distance matrix to the contents of the adjacency matrix. Then, it determines whether the current shortest path between two vertices is shorter or a path including one more intermediate vertex is shorter. It iterates N times, so that the resulting matrix contains the shortest path between vertices, with the possibility of including all other vertices as intermediate vertices. It is an O(N^3) operation. Each iteration of Floyd-Warshall can be highly data-parallel if all updates to the matrix are written to a scratch matrix, thereby not overwriting a value that another thread needs before the end of the iteration. Thus, I can once again decompose by rows. At end of each iteration, threads must synchronize and the scratch matrix becomes the current matrix for the next iteration (by manipulation of pointers, to avoid copying data).



Initial Distance Filtering
If there is a row with just one 1, in P, that vertex mapping is considered assigned. The premise of distance filtering is that if a mapping is assigned, then all other possible mappings must be consistent with the assigned mapping. For example, if Vertex 1 in graph A is definitely mapped to Vertex 2 in graph B, then we can check whether Vertex 3 in graph A can be mapped to Vertex 4 in graph B, by the following condition: shortest_distance[1,3] == shortest_distance[2,4]. The distance filter performed at this stage is a worst-case O(N^3) operation because for all rows with an assigned mapping, we must loop through the all other mappings (all remaining 1s in P). This can also be a data-parallel operation if we use a scratch permutation matrix to record updates. Therefore, decompose by rows again.

Parallel Check for Impossibility or Certainty of isomorphism
Check P for isomorphism or nonisomorphism once again. If the answer is still not certain, we are forced to enter the brute force stage.

Brute Force Search (Ullmann's Recursive Backtracking)
At this point, hopefully the permutation matrix has become very sparse (which is an expectation for the average case), so there are not-so-many permutations left to test. This is a depth-first tree traversal of the remaining permutation space (worst case N! traversals), like the wandering salesman problem. At every step in this search, we make an assumption on a mapping, and perform distance filter to see if it could possibly lead to isomorphism. [Note: The distance filter here is a smaller operation than the initial distance filter (which comes before the brute force search). It is only a O(N^2) operation, since we are only testing the assumed mapping.] If isomorphism is still possible, continue making assumptions and testing them. If isomorphism becomes impossible as the result of an assumption, we prune the remaining subtree of possible assumptions, and rollback the changes made to P from distance filtering by restoring from an undo stack. If the entire tree is traversed and no isomorphism is found, then declare nonisomorphism. The parallelism I chose to exploit here is to speed up the distance filtering step that occurs after every branch traversal/assumption made, in a manner similar to the parallelization of the initial distance filtering (as described in the previous paragraph). The advantage of this fine-grained/inner-loop parallelization is there is no worries of work imbalance or communication. The reason I did not instead parallelize the tree traversal by decomposing into independent subtrees, is because the problem differs from the wandering salesman problem in two key aspects:

The shape of the tree is irregular and unpredictable (the remaining permutation space differs depending on the input graphs and the number of branches per node of the tree is inconsistent and can only be figured out as we traverse the tree and perform the distance filter). This makes decomposition in to fix-size, independent subtrees very difficult. Also, if we cannot have independent subtrees, then threads have to communicate with each other to figure out who's working on what. It also implies arbitrary workload imbalance among threads.

Significant amount of state (a manipulated copy of the permutation matrix) needs to be kept for each thread. Each thread must also keep an undo stack. This means that for every thread I choose to employ, the memory requirement would scale linearly.

First and foremost, the program is functionally correct.

The performance metric I focus on is the scaling of the speedup of a isomorphic 1000 vertex problem, with an edge probability of 0.9 (about 90% of the vertex pairs have an edge between them) versus an increasing number of processors.



The other graph actually depicts the same metric, but as runtime vs processors. Starting at about 64 processors, the speedup starts to level off significantly. I attribute this to the problem size becoming small relative to the available threads. If we inspect the breakdown of the performance of the individual sub-algorithms, we see that most of them benefit from small scale parallelism, but as number of processors is increased past 32 processors, only the initial distance filtering and the Floyd-Warshall show good speedup (about N/2 and N/3 speedup respectively). In fact, at this threshold, the other sub-algorithms start slowing down because benefits of parallelism at this scale are smaller than the increase in thread management overhead.





Fortunately, the Floyd-Warshall and the initial distance filter largely dominate the run time, and the fact that they maintain good speedup up to 256 processors is enough to somewhat offset the degradation in the other sub-algorithms (but only up till around 64 processors). Overall, these results show the effect of Amdahl's Law... Even the simple sub-algorithms (first few preprocessing stages) which were seen to make up an insignificant piece of the overall runtime for the sequential program can become the bottleneck for a large number of processors if they do not express high enough parallelism. Another way of looking at this is to compare the run times of Floyd-Warshall and merge sort at 1 processor and 256 processors. At 1 processor, we could care less how well merge sort performance scales because Floyd-Warshall is over a thousand times slower. But at 256 processors, Floyd-Warshall run time is less than 4 times slower, which means that the fact that merge sort performance scaled poorly suddenly matters greatly in affecting the overall program run time.

I also tried to get a graph of run time versus the number of vertices by generating one pair of graphs for each case, however I got very uninformative results because the runtime of this algorithm varies greatly with the graphs I feed it, and the complexity can lie anywhere in the range between O(N^3) and O(N!). The only way to plot a meaningful graph of runtime vs vertices is to run the program for many many (possibly thousands) sets of random inputs for each number of vertices, and average over all runtimes. That is something I could not do on Blacklight (the job queues made it difficult to even get one result back within a few hours). The graph should look something like the reference plot (from my main reference paper), which depicts about O(N^3) run time (notice in log scale). The different values of 'p' shown in the graph denotes the edge probability.

Plot of run time vs nodes without averaging over many runs.. It doesn't say much..


Reference plot (supposed to look like this..) [reference 1]


1 .Main algorithm reference (non-parallel)
http://www.ece.rice.edu/~neelsh/comp482/#section3

2. Ullmann's paper that describes recursive backtracking
http://www.engr.uconn.edu/~vkk06001/GraphIsomorphism/Papers/Ullman_Algorithm.pdf

3. Floyd-Warshall algorithm description
http://www.mcs.anl.gov/~itf/dbpp/text/node35.html

I'm the only member on my team, so I did all the work. All source code was written from scratch. The other student report I referenced was only for the basic algorithm, not as a code base. Source code and example inputs/outputs