Assignment 5: Rubber Duckie

Description

In this assignment you will write Python code to generate an STL file for a rubber duck, which you will then 3D print. The duck is described using a set of nine parametric equations for ellipsoids that generate a beak, eyes, head, neck, body, wings, and tail. Your code will create a triangular mesh to approximate the surface of each ellipsoid. These meshes will be written out as an STL file. Technically this is not a valid description of a 3D object, becauses the meshes overlap rather than forming a continuous surface. But in practice, slicing programs can deal with these imperfections, so your STL file can be printed.

The 2D Case: Approximating An Ellipse

Let's start with a simpler 2D case of an ellipse centered on the origin whose major and minor axes are aligned with the coordinate axes. Such an ellipse can be described by two parametric equations for the x and y coordinates, where the parameter θ varies from 0 to 2π:

x(θ) = A cos(θ)
y(θ) = B sin(θ)

The constants A and B determine the shape of the ellipse: they are the lengths of the semi-major and semi-minor axes. If A is larger than B then A is the semi-major axis, otherwise A is the semi-minor axis. If A equals B, then the shape is a circle and A is the radius. If we want to move the ellipse off of the origin we can add in offset terms x₀ and y₀:

x(θ) = x₀ + A cos(θ)
y(θ) = y₀ + B sin(θ)

If we want to tilt the ellipse so its major and minor axes are not aligned with the coordinate axes, we could introduce additional terms in the equations, but this won't be necessary for our purposes.

To draw the ellipse, we use the equations to generate a set of points (x_i,y_i) by stepping θ from 0 up to 2π. We can then draw lines to connect adjacent points. Here is an ellipse defined by A=2 and B=1:

Since our goal is to generate a triangular mesh, we will instead use the points to generate a set of triangles. Each triangle will have one point at the center of the ellipse; the other two points will approximate the edge: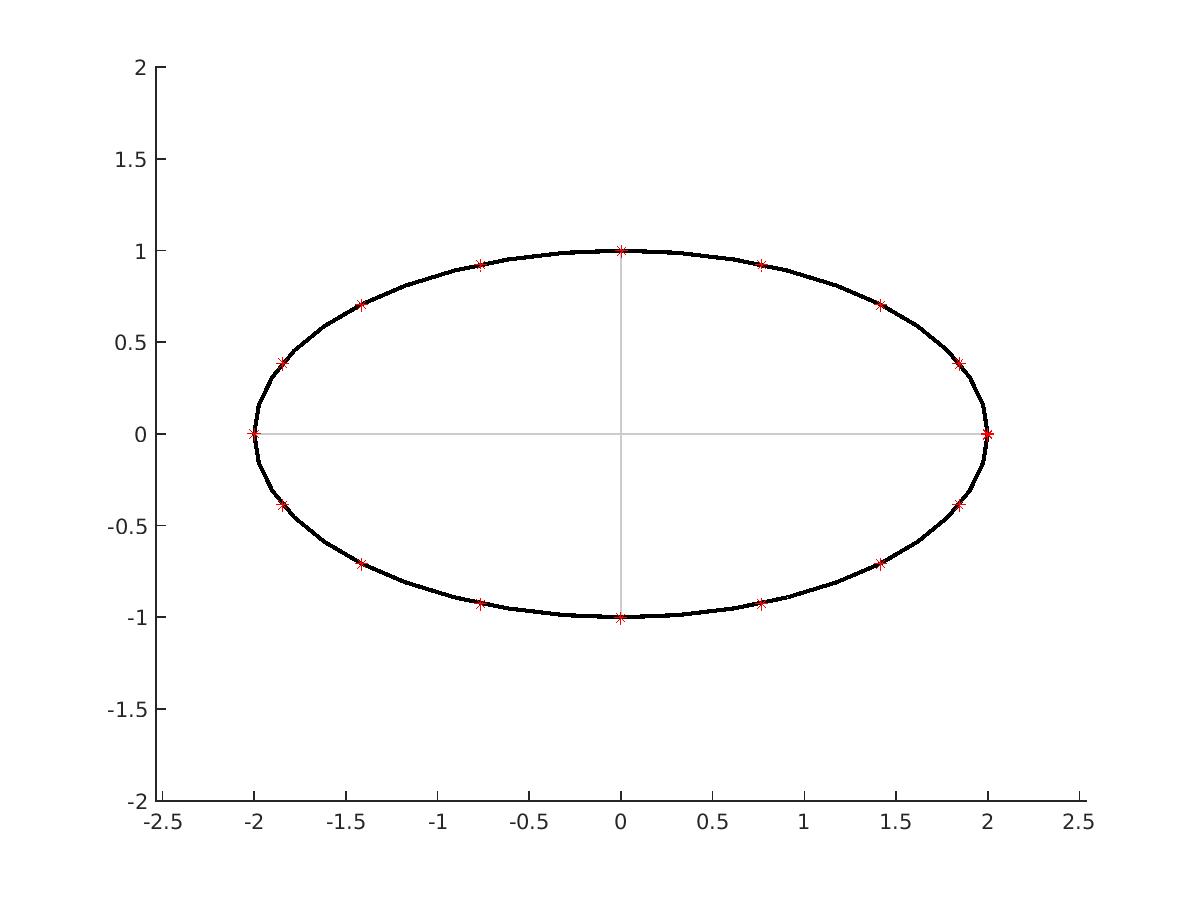

By using a smaller step size dθ we can generate more points and get a finer approximation to the true curve:

Here is sample code ellipse_example.py to generate the ellipse and write out the STL file ellipse.stl. This code relies on the stlwrite package.

After writing out the triangles as an STL file we can examine it in MeshLab. Play with the mode buttons at the top of the MeshLab window to view the triangulation with or without shading.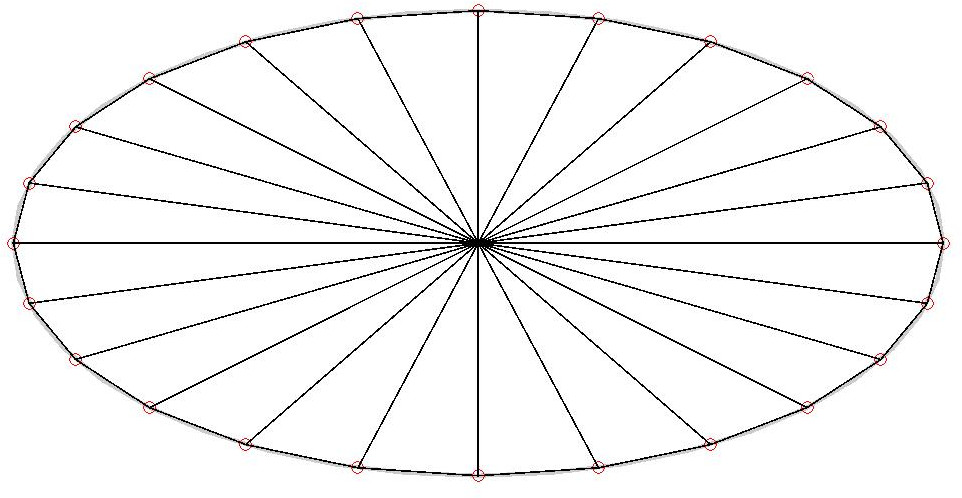

The 3D Case

The higher-dimensional generalization of an ellipse is called an ellipsoid. In 3D an ellipsoid can resemble a football. There are three parameters governing the lengths of the axes, which we'll denote A, B, and C. We'll be using spherical coordinates for our parametric equations, so instead of a single angle θ there are two angles, θ and φ. θ ranges from 0 to 2π as before, while φ ranges from -π/2 to +π/2. You can think of these parameters as longitude and lattitude, with φ=+π/2 being the north pole and φ=-π/2 being the south pole.

The 3D parametric equations for an axis-aligned ellipsoid are:

x(θ, φ) = x₀ + A cos(θ) cos(φ)
y(θ, φ) = y₀ + B sin(θ) cos(φ)
z(φ) = z₀ + C sin(φ)

For any given φ value, the steps of θ trace out an ellipse (a parallel of lattitude) parallel to the x-y plane. For the next lattitude value, φ+dφ, there is another ellipse just below it. If we pick two adjacent points on the first ellipse, and the corresponding two adjacent points on the second ellipse, we'll have a quadrilateral surface patch, as in the diagram above. The Python code for generating an STL file will automatically split this quadrilateral into two triangular patches.

The only exceptions are at the north and south poles, where φ = ±π/2, so cos(φ) is zero, so x = x₀, y = y₀, z = z₀ ± C, and the ellipse becomes a point. In these two special cases our surface patches connecting level φ with level φ+dφ are triangles instead of quadrilaterals.

Given this explanation, write a Python function get_ellipsoid that takes parameters A, B, C, x₀, y₀, and z₀ as input and returns a list of triangular and quadrilateral surface patches. You will need to use a nested for loop to iterate over values of θ and φ.

Test your function by writing out the patches as an STL file and viewing the file in MeshLab.

Note: the order of vertices should be clockwise to indicate which side of the patch is the exterior surface of the object. If you get this order wrong, Meshlab will render the patch as flat black instead of shaded.

Describing the Duck

Here are the parameter values for the nine ellipsoids that describe the duck:

Part A B C x₀ y₀ z₀
beak 0.4 1 0.2 0 -0.3 π 0.5 π

head 1 1.2 1 0 0 0.5 π

left eye 0.15 0.2 0.15 0.23 π -0.15 π 0.62 π

right eye 0.15 0.2 0.15 -0.23 π -0.15 π 0.62 π

neck 0.75 0.75 1 0 0.5 0.5

body 2 3 1.2 0 0.75 π 0

left wing 0.2 1.4 0.6 0.56 π 0.8 π 0

right wing 0.2 1.4 0.6 -0.56 π 0.8 π 0

tail 0.8 1.4 0.2 0 1.4 π 0.1 π

You should write all nine ellipsoids into the same STL file. The result should look something like this:

Modify the parameters a bit to customize your duck. Print out your duck on the Cube.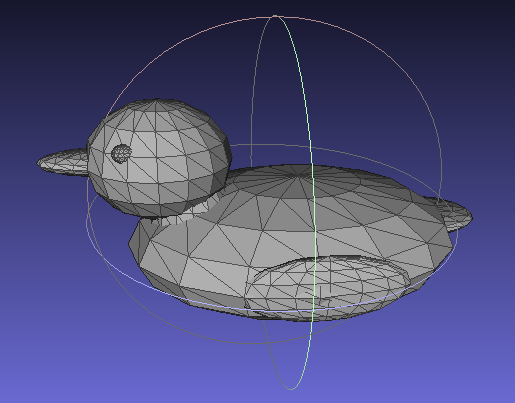

What to Hand In

Collect the following into a zip file and submit via AutoLab:

Your Python source code.
The STL file that is the output of your code with your modified parameters.
A screen capture showing a rendering of your generated STL file. You can use Meshlab for the rendering, or you can use some other program, such as the Cube Client program.

Also post a photograph of your 3D printed customized duck to Piazza.

Dave Touretzky

Last modified: Sat Feb 13 14:34:11 EST 2016