A Proof Technique

 

There are two major steps in the proof technique for showing one machine satisfies another.

1. The Creative (Intellectually Hard) Step.
   • Define an abstraction function

     

     to relate concrete states with abstract states.
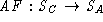
   • Define a representation (sometimes called concrete) invariant,

     

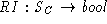
     that characterizes the domain of AF. This predicate prunes down the set of concrete states, 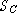, to only those of interest (only those that represent some abstract state in 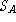). After you define this predicate, you must prove that it indeed is an invariant. You may use the technique presented in the Reasoning About State Machines handout to show this.
2. The Checklist (Tedious) Step.
   • For each 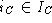(for all initial states in 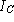) show:

     

     This requires showing that each initial state of the concrete machine is some initial state of the abstract machine.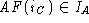
   • For each state tr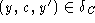ansition of the concrete machine C where y satisfies RI, there must exist a state transition 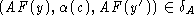of the abstract machine A. To show this, it suffices to show the following commutative relationship holds:
     
     

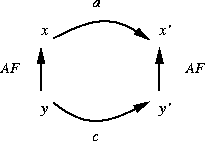
     where x = AF(y), x' = AF(y') and 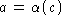. Here's how to read the diagram: Put both index fingers at the concrete state y; move your right one to the right (performing the concrete action c) and then up (applying AF to the new concrete state y'); move your left one up (applying AF to y) and then to the right (performing the corresponding abstract action 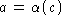; you should end up in the same place: the abstract state, x'.

Please brand this commuting diagram on your brain.