- First, I define
an abstraction function.

AF(0) = sun
AF(1) = mon
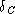
AF(6) = satNotice that, as promised, it's one-to-one.
- Next, I define the representation invariant.
I note that I don't need all integers
to represent the days of the week. I only need seven. Moreover, the
transition function,
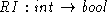 is defined for only those seven.
is defined for only those seven.
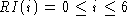
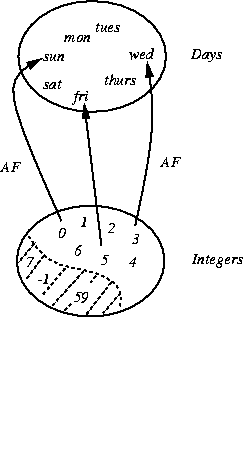
The representation invariant just says that the only integer values I have to worry about are between 0 and 6 inclusive. It characterizes the domain of AF.
- Initial conditions: I need to show
that each initial state of Mod7Counter is an initial
state of Day (under the abstraction function).
- 0 is the initial state for the Mod7Counter. Thus, AF(0) had better be some initial state of Day. Indeed, AF(0) = sun, the initial state of Day.
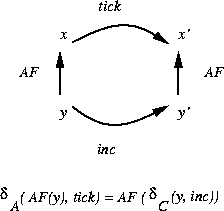
- Commuting diagram: I need to show it holds for each action of Mod7Counter.
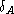
In other words, I need to show
 that
that
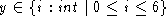 for all y
that satisfy the representation invariant, i.e., for all
for all y
that satisfy the representation invariant, i.e., for all 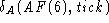 .
I need to show the commuting diagram for only those states that
satisfy RI.
The simplest proof is to do an exhaustive case analysis.
y can take on only seven values so there are seven cases. I'll
do the most ``interesting'' case (y = 6).
.
I need to show the commuting diagram for only those states that
satisfy RI.
The simplest proof is to do an exhaustive case analysis.
y can take on only seven values so there are seven cases. I'll
do the most ``interesting'' case (y = 6).
- Case: y = 6
 ¯
¯
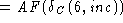 def'n of AF
def'n of AF
= sun def'n of
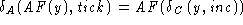
= AF(0) def'n of AF
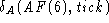 def'n of
def'n of 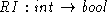
- Case: y = 6