Loss Function

Loss function is used to measure the degree of fit. So for machine learning a few elements are:

  1. Hypothesis space: e.g. parametric form of the function such as linear regression, logistic regression, svm, etc.
  2. Measure of fit: loss function, likelihood
  3. Tradeoff between bias vs. variance: regularization. Or bayesian estimator (MAP)
  4. Find a good h in hypothesis space: optimization. convex - global. non-convex - multiple starts
  5. Verification of h: predict on test data. cross validation.
Among all linear methods $y=f(\theta^Tx)$, we need to first determine the form of $f$, and then finding $\theta$ by formulating it to maximizing likelihood or minimizing loss. This is straightforward.

For classification, it's easy to see that if we classify correctly we have $y\cdot f = y\cdot \theta^Tx\gt0$, and $y\cdot f = y\cdot\theta^Tx\lt0$ if incorrectly. Then we formulate following loss functions:

  1. 0/1 loss: $\min_\theta\sum_i L_{0/1}(\theta^Tx)$. We define $L_{0/1}(\theta^Tx) =1$ if $y\cdot f \lt 0$, and $=0$ o.w. Non convex and very hard to optimize.
  2. Hinge loss: approximate 0/1 loss by $\min_\theta\sum_i H(\theta^Tx)$. We define $H(\theta^Tx) = max(0, 1 - y\cdot f)$. Apparently $H$ is small if we classify correctly.
  3. Logistic loss: $\min_\theta \sum_i log(1+\exp(-y\cdot \theta^Tx))$. Refer to my logistic regression notes for details.
For regression:
  1. Square loss: $\min_\theta \sum_i||y^{(i)}-\theta^Tx^{(i)}||^2$
Fortunately, hinge loss, logistic loss and square loss are all convex functions. Convexity ensures global minimum and it's computationally appleaing.


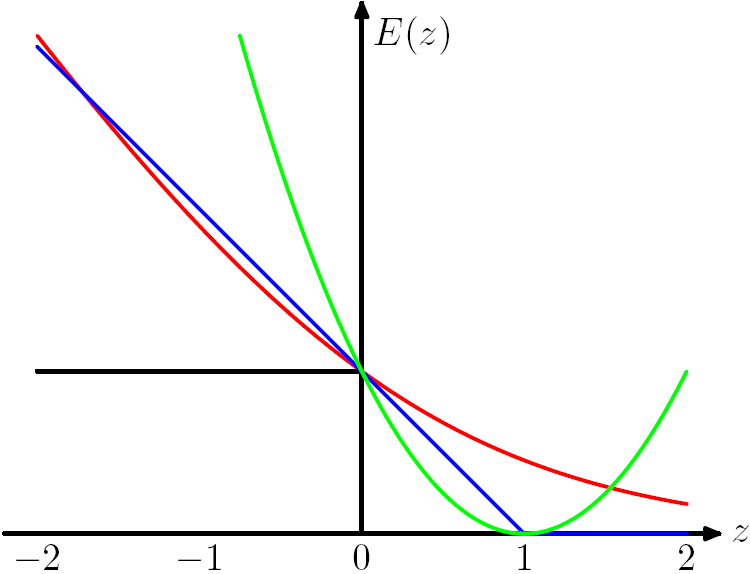
Figure 7.5 from Chris Bishop's PRML book. The Hinge Loss E(z) = max(0,1-z) is plotted in blue, the Log Loss in red, the Square Loss in green and the 0/1 error in black.
Copied from https://research.microsoft.com/en-us/um/people/manik/projects/trade-off/hinge.html