Finite State Machines - Exercises 1

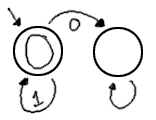
Following are some exercises on finite state machines. You should attempt to work through these before checking the answers.

For the problems in this section, draw a deterministic finite state machine which implements the specification. Some machines may be impossible to construct; explain why if you think so. Where appropriate, the alphabet (allowable input characters) for the machine is listed [in brackets]. It's not important to be precise about every transition; it is sufficient to draw an unadorned arrow to mean "all other characters". Remember to indicate the starting state.

1. Consider machines which accept a stream of 1 or more bits (the alphabet is limited to 1's and 0's), and whose output is 1 (accepting) or 0 (rejecting). Construct FSMs which implement the following operations:

(a) or
That is, the output should equal the C expression

c₁ || c₂ || ... || c_i




(b) and
c₁ && c₂ && ... && c_i


(c) xor
c₁ ^ c₂ ^ ... ^ c_i

2.

(a) Accepts just the string MURMUR by itself. [MRU]

(b) Accepts CYBOT followed by any characters. [BCOTY]

(c) Accepts FROG with any prefix. [FGOR]
Be careful. Does your machine accept FROFROG?

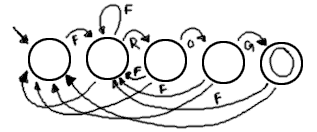(d) Accepts any string containing FROG. [FGOR]

(e) Accepts any string containing MURMURS. [MRSU]

(f) Accepts strings consisting of only 0 or more repetitions of 15211. [125]

(g) Accepts strings starting with 0 or more repetitions of 15211. [125]

(all strings start with 0 or more repetitions of 15211.)

3.

(a) Accepts CAT or DOG alone. [ACDGOT]

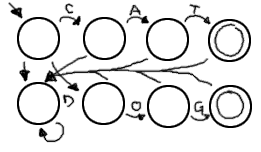(b) Accepts strings containing CAT or DOG anywhere. [ACDGOT]

(c) Accepts strings containing ART or ARC anywhere. [ACRT]

(d) Accepts strings which are any of ART or ARTS or ARTIST or ABLE. [ABEILRST] What does this remind you of?

4. #c means the number of character c occuring in the string.

(a) Accepts strings of even length. [AB]

(b) Accepts strings with exactly 3 A's. [AB]

(c) Accepts strings with at least 3 A's. [AB]

(d) Accepts strings where #a > #b. [AB]

Impossible. Since #a is unbounded, this machine would need an infinite amount of states, or some infinite auxilliary storage. A counting argument shows why: Since at any point in the processing of the string we can encounter any number of B's, we'd need to keep track of the number of A's encountered so far. This is an unbounded number. In order for a machine to keep track of exactly how many A's we've had, we'd need at least one state for each possibility. But there are an infinite number of possibilities for #a, so we can't do this with a finite state machine.

(e) Accepts strings where #a = #b. [AB]

Impossible. Since the A's and B's can come in any order, this can't be done for the same reason as 4d.

(f) Accepts strings where (#a mod 3) = (#b mod 3). [AB]

( Tom 7's page )