15110 Fall 2011 [Cortina/von Ronne]
Lab 11 - Sorting Networks and Minimum Spanning Trees
You may work on this lab with another student if you wish.
If you do, put a comment in the program code that includes both
of your names, and both of you should submit the code.
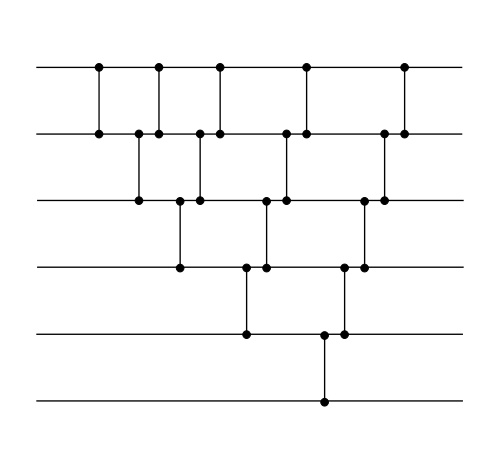
Sorting Networks
To the right is a wiring diagram for a sorting network that will
sort six values. Each vertical line represents a comparison element
with its inputs coming in from the left and outputs being sent out
to the right.
On paper, trace the operation of this sorting network on the input
2, 8, 3, 9, 0, 7. (If your CA gives you a different input, use
it instead.)
Which comparisons in this diagram can be performed concurrently?
How many steps does it take to sort concurrently?
(record your answer on paper)
Do you recognize the sorting algorithm? What is it?
Minimum Spanning Trees
The following algorithm can be used to find the minimum spanning
tree of a graph:
- Set n equal to the number of nodes in graph.
- Set pq equal to a new array of size n. Then initialize each element
at the index \(i\) to the value \(i\). (That is, set pq[0] = 0, pq[1] = 1, etc.)
- Set cost equal to a new array of size n. Then initialize each
element in this array to Infinity.
- Set parent equal to a new array of size n. You do not need to
initialize this array.
- While the length of the array pq is greater than 1, do the following:
- Remove the first element from the array pq and set current
equal to this value.
- For every element i in array pq do the following:
- Set w equal to the weight (stored in graph) of the
edge from current to i.
- Set c equal to cost[i]
(the cost for connecting node i to the spanning tree).
- If w < c then do the following:
- Set parent[i] equal to current.
- Set cost[i] equal to w.
- Sort the elements of pq according to the value obtained, for
each element x of pq, by calculating cost[x].
Set pq equal to this sorted array.
- Return the array parent as the final result.
Consider the graph represented by the Ruby expression (where
inf was previously set to 1/0.0):
[[0,8,inf,inf,4],
[8,0,3,inf,6],
[inf,3,0,9,5],
[inf,inf,9,0,7],
[4,6,5,7,0]]
On paper draw the graph represented by this matrix.
On paper, trace the execution of applying the minimum spanning
tree algorithm to the graph described by the matrix above.
What are the final elements of the parent array?
What do those elements mean? Draw the resulting tree on paper.
Deliverables
Hand in the paper with your work.
