S S = S
| D D = D
| a d = (cons a d)
![]()
S = S
| D = D
| (cons a d) = a
Say the binding time of s were S and d were D in the
following code:
(prim p cons s d) (prim x car p)and assume
cons were treated as a generic primop (ie x would be D, even though we can deduce its value
at compile time by using the semantics of cons and car.
To do this, first allow partially static binding times:
bt ::=and defineS|D| (cons bt bt)
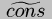
SS=S|DD=D| a d = (cons a d)
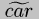
S=S|D=D| (cons a d) = a
In the above example, p would then be assigned the partially
static binding time (cons , and S D)x would be S.
![]() is defined similarly.
is defined similarly.
These new binding times are ordered as follows to make a lattice:
S< (cons a d) <D(cons a1 d1) <= (cons a2 d2) <==> a1 <= a2 and d1 <= d2
S and D are still bottom and top, but between them lie the
partially static binding times.
Ok, that much is easy, but it has a serious problem: the lattice now contains infinite ascending chains. Eg
S< (consSD) < (cons (consSD)D) < (cons (cons (consSD)D)D) ...
This happens if the source program recurses over a potentially
unbounded data structure. The BTA could detect this conservatively
and lift the offending value to D, but this loses too much
information (see envs). Instead, directed graphs are used to abstract
partially static values of unbounded size.
Since there are only a finite number of cons instructions in the
source program, one of them must be repeated in the BTs of an
ascending chain. Such a BT can be widened [Cousot] by
merging the duplicate nodes, and joining the children. We label the
cons nodes so that duplicates can be identified:
bt ::=S|D| (cons bt bt cp) cp ::= instruction
Cp stands for cons point, it is represented with a
pointer to the root source instruction where this cons is created.
Cons points are denoted with the name of the variable bound to the
cons cell, eg the binding time of p above is written (cons .
S
D p)
Thus if two nodes with the same cons point (say (cons a1 d1 p) and (cons a2 d2 p)) appear in a binding time,
then that BT can be widened by replacing them with the single node (cons (.
![]() a1 a2) (
a1 a2) (![]() d1 d2) p)
d1 d2) p)
The formal definition of the ordering of the lattice is now:
S< (cons a d ...) <D(cons a1 d1 cp1) <= (cons a2 d2 cp2) <==> a1 <= a2 and d1 <= d2 and cp1 = cp2
By collapsing all nodes with duplicate cons-points, infinite ascending chains can be avoided, guaranteeing termination (see envs).
One of these new binding times is a graph grammar dividing a data structure into static and dynamic portions. Sometimes an atom is identified as partially static by the grammar, but this is allowed since in abstract interpretation we only need approximate actual values, and any partially static value approximates a purely static one.
The quality of an abstraction is measured by how well it matches the distinctions required between typical programs. Grammars have proven tremendously effective in capturing information about data structures with finite descriptions. [Mogensen89] first applied grammars to partially static structures, the techniques was later refined in [Consel90] and [Consel93].
Implementations of partially static structures usually have to be careful to avoid the following unsound reduction:
(cdr (cons (printf D) 23)) --> 23
But in continuation-passing style, arguments to prims are variables
not expressions, so there is no danger in eliminating them. Instead
I plan to do all dead code elimination in the backend.