At various times a join in the abstract interpretation of the binding times loses information. This causes a variable to be lifted from one binding time to another. Simple cases are handled directly by cogen, but with partially static and circular binding times, lifting can be much more complex. This section describes how cogen uses itself to create lift compilers to handle complex lifting.
Some lifts are handled directly by cogen; these are primitive
lifts. Eg, a lift from S to D causes a constant declaration to be
generated by the compiler; the value of the constant is the static
value, held in a local variable in the generated compiler. There is
also the primitive higher-order lift, described below.
Consider the compiler for lifting (cons (cons to S D) (cons S
D))D. In lisp, the compiler would look like [note compile]
(lambda (lift-bt-comp s-vals) (compile `(lambda (d-vals) (cons (cons ,(car s-vals) (car d-vals)) (cons ,(cdr s-vals) (cdr d-vals))))))
This example belies how hard lifting is in general: circular binding times, variable splitting, and higher-order lifting all make this harder. Fortunately, there is a nice way to handle all of this by using cogen itself. First define lift inductively (ignore higher-order procedures for a moment):
(define (lift bt-from bt-to val)
(match (list bt-from bt-to)
(('static 'dynamic)
(primitive-lift val))
((x 'static) val)
(('dynamic x) val)
(else (if (pair? val)
(let ((a (lift (bt-car bt-from)
(bt-car bt-to)
(car val)))
(d (lift (bt-cdr bt-from)
(bt-cdr bt-to)
(cdr val))))
(cons a d))
val))))
(define bt-car ...) ; = 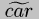 (define bt-cdr ...) ; =
(define bt-cdr ...) ; = 
[note match]
This procedure copies val while traversing the binding times in
parallel fashion. When the binding times indicate that we have
reached a part of val that must be lifted, then the primitive lift
is applied. If we execute this procedure, it would only copy the
value. Instead, use the lift compiler
(code lift (bt-from bt-to val k) ...)to create a procedure specialized to particular binding times:(define lift-compiler (cogen lift '(static static dynamic dynamic)))
; lifter = (define lift-bt (eval-root lift-compiler (list tlc from to)))
This procedure lifts the right parts of val, but the control flow
based on the binding-times has been eliminated. Control flow based on
val will remain because of the pair? in the recursive case.
But it's still just a copier.
At the point of the lift, a call to this procedure is inserted into
the source instruction list. cont finishes the intructions list,
it takes the lifted value and the live variables as arguments. So
when cogen reaches this procedure call, another compiler is generated:
(define cl-bt (cons (const cont) live-vars-bt)) (define lift-bt-comp (cogen lift-bt (list bt-from cl-bt)))
This is exactly what we had above. It's interesting how the static
data remaining in bt-from is passed to cont. The control flow
from the pair? calls remains only where there was a loop in the
binding times (see spines) [how does this relate to memoizing
compilers only where required?]
Higher-order lifts can be handled by adding an addition case to lift that invokes cogen's primitive higher-order lift. Also when it
conses up the result, it must use closure-cons as appropriate.
So when cogen encounters a non-primitive lift, it inserts a procedure
call to a specialized version of lift into the source code, and
cogens this instead. The lift compiler is a good example of three (it
will be four when the general lift is written in mini-scheme instead
of root) layer composition (see layers).
Lifting a atom to a partially static binding time requires replicating the atom in both binding times (think of splitting an environment into two lists, each has its own terminating nil). This atom must be copied.
I think the lift compiler might simplify things enough that it could be used to support direct implementation of a multistage cogen, instead of using multipass.