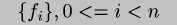Mathematically, an IFS is defined by a finite set of functions 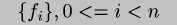on a space ie . These functions (typically between two and five) define a subset by the following recursive set equation: P is the recursive picture. But given the functions, how can one solve the equation and produce the picture?

Note that if then , thus if we have some of P, then we can get more of P. And not just one more point: so too are etc in P. To get all of P we must consider every possible string of applications. Thus the IFS algorithm

draw point x
pick random i
x = f[i](x)
repeat

But how do we get the first point in P? As long as the functions are contractive, then the above algorithm will work given any x because P is an attractor. You only have to throw out the initial dozen or so iterations while x settles into the fractal.

furthermore, this gives us more than just membership in the set, it gives density: how likely are we to see the point (or one very near it) as the algorithm runs?

Coloring an IFS

a monochrome histogram viewed with a colormap works ok (bomb uses this), but it's possible to do better.

add another dimension to the IFS, and map this value. This coordinate is independent of the others, and its functions are very simple: the first function of the set averages the color value with zero, the other functions average it with one. The colormap value of a point is then simply the base-two interpretation of the string of function choices made by the IFS algorithm, a number between zero and one (the most recent digit has most significance). libifs.c:98

The advantage of this scheme is that the coloring is structural. The disadvantage is that the histogram must now be three channels (RGB) instead of one. Note that the log only applies to intensity, so the RGB values are transformed into YUV coordinates, and the log is applied to Y only.

an alpha channel has also been implemented.