Parallel Models of Computation

Developing a standard parallel model of computation for analyzing algorithms has proven difficult because different parallel computers tend to vary significantly in their organizations. In spite of this difficulty, useful parallel models have emerged, along with a deeper understanding of the modeling process. In this section we describe three important principles that have emerged.

1. Work-efficiency. In designing a parallel algorithm, it is more important to make it efficient than to make it asymptotically fast. The efficiency of an algorithm is determined by the total number of operations, or work that it performs. On a sequential machine, an algorithm's work is the same as its time. On a parallel machine, the work is simply the processor-time product. Hence, an algorithm that takes time t on a P-processor machine performs work W = Pt. In either case, the work roughly captures the actual cost to perform the computation, assuming that the cost of a parallel machine is proportional to the number of processors in the machine. We call an algorithm work-efficient (or just efficient) if it performs the same amount of work, to within a constant factor, as the fastest known sequential algorithm. For example, a parallel algorithm that sorts n keys in 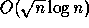time using 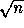processors is efficient since the work, 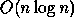, is as good as any (comparison-based) sequential algorithm. However, a sorting algorithm that runs in 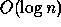time using processors is not efficient. The first algorithm is better than the second - even though it is slower - because it's work, or cost, is smaller. Of course, given two parallel algorithms that perform the same amount of work, the faster one is generally better.

2. Emulation. The notion of work-efficiency leads to another important observation: a model can be useful without mimicking any real or even realizable machine. Instead, it suffices that any algorithm that runs efficiently in the model can be translated into an algorithm that runs efficiently on real machines. As an example, consider the widely-used parallel random-access machine (PRAM) model. In the PRAM model, a set of processors share a single memory system. In a single unit of time, each processor can perform an arithmetic, logical, or memory access operation. This model has often been criticized as unrealistically powerful, primarily because no shared memory system can perform memory accesses as fast as processors can execute local arithmetic and logical operations. The important observation, however, is that for a model to be useful we only require that algorithms that are efficient in the model can be mapped to algorithms that are efficient on realistic machines, not that the model is realistic. In particular, any algorithm that runs efficiently in a P-processor PRAM model can be translated into an algorithm that runs efficiently on a 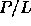-processor machine with a latency L memory system, a much more realistic machine. In the translated algorithm, each of the 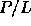processors emulates L PRAM processors. The latency is ``hidden'' because a processor has useful work to perform while waiting for a memory access to complete. Although the translated algorithm is a factor of L slower than the PRAM algorithm, it uses a factor of L fewer processors, and hence is equally efficient.

3. Modeling Communication. To get the best performance out of a parallel machine, it is often helpful to model the communication capabilities of the machine, such as its latency, explicitly. The most important measure is the communication bandwidth. The bandwidth available to a processor is the maximum rate at which it can communicate with other processors or the memory system. Because it is more difficult to hide insufficient bandwidth than large latency, some measure of bandwidth is often included in parallel models. Sometimes the specific topology of the communication network is modeled as well. Although including this level of detail in the model often complicates the design of parallel algorithms, it's essential for designing the low-level communication primitives for the machine. In addition to modeling basic communication primitives, other operations supported by hardware, including synchronization and concurrent memory accesses, are often modeled, as well as operations that mix computation and communication, such as fetch-and-add and scans. A final consideration is whether the machine supports shared memory, or whether all communication relies on passing messages between the processors.