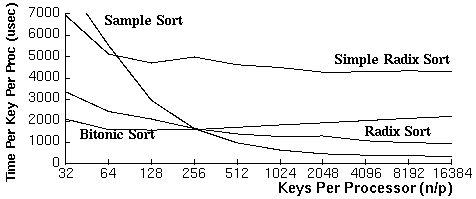
Radix Sort for Vector Multiprocessors: We have implemented an efficient fully vectorized and parallelized radix sort algorithm for the Cray Y-MP. On one processor of the Y-MP, our sort is over 5 times faster on large sorting problems than the optimized library sort provided from Fortran. On eight processors we achieve an additional speedup of almost 5, yielding a routine over 25 times faster than the library sort. Using this multiprocessor version, we can sort at a rate of 15 million 64-bit keys per second.
Our Supercomputing'91 paper (by Marco Zagha and Guy Blelloch) describes the parallel radix-sort algorithm, introduces some techniques for mapping parallel algorithms onto vector multiprocessors, discusses our implementation of the radix-sort on the Y-MP, and derives equations to predict and optimize the performance of the sort. The most interesting elements of the implementation are a vectorized and parallelized histogram operation, a vectorized and parallelized scan (all-prefix-sums) operation, and a memory access pattern designed to avoid memory bank conflicts. The algorithm is adapted from a data-parallel algorithm previously designed for a highly parallel Single Instruction Multiple Data (SIMD) computer, the Connection Machine CM-2.
The NAS benchmark report includes Integer Sort benchmark timings of our Cray Y-MP/C90 implementation, which is currently the fastest reported for any machine. Our implementations were developed on the Cray Y-MP and Cray Y-MP/C90 at the Pittsburgh Supercomputing Center. Our sorting code for the Cray Y-MP family (written in Cray assembly language) is publicly available.
Merging on Vector Multiprocessors: Marco Zagha is currently working on a fast implementation of a PRAM merging algorithm for the Cray C90. For large input vectors, the implementation is significantly faster than bitonic merge because the PRAM algorithm performs linear work while bitonic merge performs nlog(n) work. Our implementation also outperforms a serial merge because it makes efficient use of vector instructions and can take advantage of multiple processors.
Sorting and Merging in NESL: We have coded several sorting algorithms (quicksort, bitonic-sort, odd-even-merge-sort) in NESL. For example, here is the quicksort implementation:
function qsort(a) =
if (#a < 2) then a
else let pivot = a[#a/2];
lesser = {e in a| e < pivot};
equal = {e in a| e == pivot};
greater = {e in a| e > pivot};
result = {qsort(v): v in [lesser,greater]};
in result[0] ++ equal ++ result[1] $