| We
deal with the problem of allocating resources to tasks under their
various constraints of quality of service (QoS) requirements.
Resources can be homogeneous (e.g., processors in
multi-processor-based systems) or heterogeneous (e.g., processor,
disk, network). This can be applied to distributed embedded,
real-time and multimedia systems. Each task has various resource
requirements along its each QoS dimension. For example, a video
conferencing application can have the following QoS dimensions viz.,
frame rate, resolution, security etc. Our goal is to derive scalable
near-optimal results on resource-allocations of QoS-aware tasks.
Resources
QoS
Summary
of Q-RAM:
Our approach is based on Q-RAM (QoS-based Resource Allocation
Model). It is an analytical approach for satisfying multiple
quality-of-service dimensions in a resource-constrained environment.
Using this model, available system resources can be apportioned
across multiple applications such that the net utility that accrues
to the end-users of those applications is maximized.
Application
Context
Multimedia
systems using audio and video streams can provide better audio/video
quality at higher resolution and/or very low end-to-end delays.
Tracking applications can track objects at higher precision and
accuracy if radar tracks are generated and processed at higher
frequencies. In many cases, computationally intensive algorithms can
provide better results than their less-demanding counterparts. Even
interactive systems can provide excellent response times to users if
more processing and I/O resources are made available. Conversely,
many applications can still prove to be useful and acceptable in
practice even though the resources needed for their maximal
performance are not available. For instance, a 30 frames/second
video rate would be ideal for human viewing, but a smooth 12 fps
video rate suffices under many conditions. The QoS-based Resource
Allocation Model (Q-RAM) addresses the following question: "how
does one allocate available resources to multiple concurrent
applications?".
Q-RAM
Novelty
The novelty of
Q-RAM is that it allows multiple Quality of Service requirements
such as timeliness, cryptography and reliable data delivery to be
addressed and traded off against each other. It also allows
resources to be traded off against each other to obtain the same
level of QoS along a particular dimension. For example, video at a
certain frame rate can be transmitted in raw form, consuming minimal
CPU cycles and high network bandwidth. Alternatively, the video can
be compressed, consuming significant CPU cycles but consuming less
network bandwidth. Q-RAM provides a framework to make such resource
and QoS tradeoffs across multiple applications. Both discrete and
continuous QoS dimensions have been studied.
System
Model
The QoS architecture [7]
we consider is composed of a QoS specification interface, a quality
trade-off specification model, and a unified QoS-based admission
control and resource allocation model. The QoS specification allows
multiple QoS requirements to be specified. The trade-off model
allows the applications and the users to assign quantitative values
called ``utilities'' to the different levels of service. Finally, a
QoS resource manager makes resource allocations to those
applications so as to maximize the global utility as a weighted sum
of the utilities of the individual applications.
In [7],
we presented a QoS management framework that enabled system
developers and application developers to quantitatively define QoS,
and to analytically plan and allocate resources. The system
resources are distributed among multiple applications of different
quality levels such that the net utility that accumulates to the
end-users is maximized.
Using this architecture, the problem of maximizing system utility
by allocating a single finite resource and multiple
finite resources to satisfy the QoS requirements has been studied in
[7]
and [5]
respectively. It was also proved in [5]
that an optimal solution for allocation of multiple resources is
NP-hard.
In this project, we consider a more refined problem of
apportioning multiple resources with many choices on
resource-types. We then present three solutions to the problem. All
these solutions are the variants of the local search technique for multiple
resource multiple-dimension scheme presented in [5].
We consider a distributed system with multiple resources
that services n independent applications denoted by 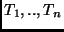 .
There are m shared resources which are allocated across .
There are m shared resources which are allocated across 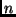 applications. The resources could be of same or of different types,
such as processors (as sources of computation) or network links (as
sources of network bandwidth). We let
applications. The resources could be of same or of different types,
such as processors (as sources of computation) or network links (as
sources of network bandwidth). We let 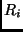 denote the set of possible allocation choices for the
denote the set of possible allocation choices for the 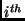 resource. Each of the shared resources has a maximum quantity or
size denoted by
resource. Each of the shared resources has a maximum quantity or
size denoted by
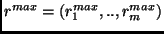 .
Each application or task has a quality of service (QoS) requirements
across one or many dimensions. For example, a video conferencing
application can have the dimensions such as Cryptographic security,
Data delivery reliability, video related quality (resolution, frame
rate etc.) and audio related quality (sampling rate, audio
timeliness etc.). .
Each application or task has a quality of service (QoS) requirements
across one or many dimensions. For example, a video conferencing
application can have the dimensions such as Cryptographic security,
Data delivery reliability, video related quality (resolution, frame
rate etc.) and audio related quality (sampling rate, audio
timeliness etc.).
An user derives satisfaction through these various
qualities. Higher the quality along any dimension, higher is the
satisfaction. We quantify this in the form of a parameter called utility.
The value of this parameter along different quality dimension
depends on the application as well as the user. For example, for a
fast-moving video application, the frame rate may provide higher
utility to the user than the resolution. It may reverse if it
happens to be very slow-moving video. Depending on the constraints
of various resources, we may need to make trade-offs among
these different quality-dimensions.
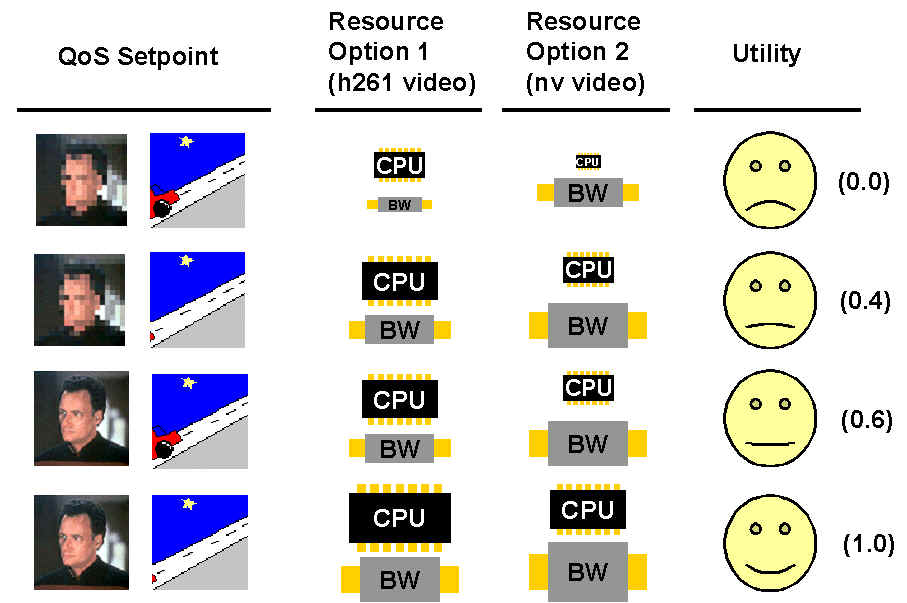
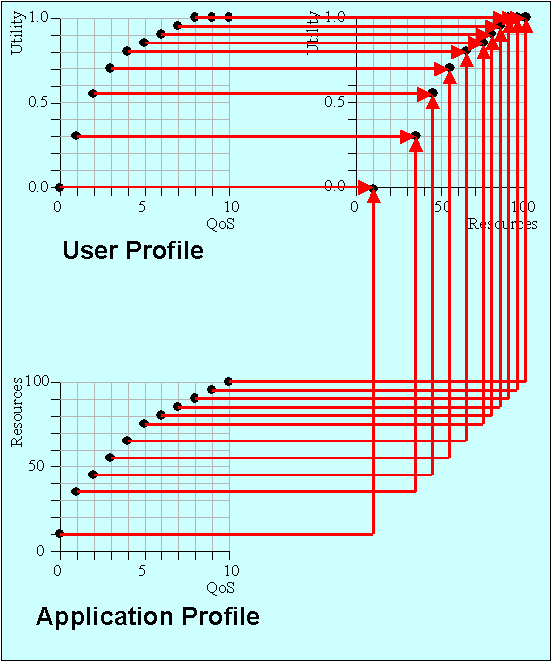
Thus, we have application profile that is divided into two
components, viz., QoS profile and Resource profile. The QoS profile
has the following components:
- Quality Space:

- Quality Index: For the jth component if
 we define a bijective function,
we define a bijective function,  which maps to the elements of
which maps to the elements of 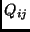 into integer valued labels, i.e.
into integer valued labels, i.e.

The labels preserve the quality ordering so that  is better than
is better than  if
if
 . .
- Dimension-wise Utility:
 ,
a numerical assessment of the utility achieved by setting ,
a numerical assessment of the utility achieved by setting
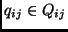 for application
for application 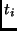 on quality dimension j.
on quality dimension j.
- Application Utility: a utility or quantitative measure
associated with application
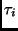 . .
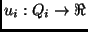
The function 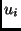 could, for example, be defined as a weighted sum of
could, for example, be defined as a weighted sum of 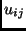 . .
The resource profile for a task defines the relation
between resource 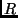 and
and  , ,
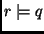 .
This is a list of resource allocation combinations that can be used
to achieve a certain level of QoS point .
This is a list of resource allocation combinations that can be used
to achieve a certain level of QoS point 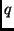 .Since
there is a combination of resources that can give rise to the same
quality point .Since
there is a combination of resources that can give rise to the same
quality point 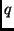 ,
we define a relation between ,
we define a relation between 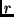 and
and 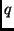 instead of a function.
instead of a function.
In addition to Application Profile, each task has a User
Profile. This dictates the user-specific quality requirements
associated with a particular session. An User profile could
be a collection of a few templates supplied with the Application
profile.
The application utility 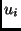 for a task
for a task 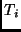 is defined as a sum of the utilities (or values) accrued when
is defined as a sum of the utilities (or values) accrued when 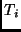 achieves certain qualities across different dimensions, i.e.,
achieves certain qualities across different dimensions, i.e.,
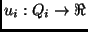 .
An application utility is defined to be weighted sum of
dimension-wise utilities. .
An application utility is defined to be weighted sum of
dimension-wise utilities.
A system utility, on the other hand, is the combined
utilities of all the applications. It can be defined as a weighted
sum of all application utilities for ``differential services'',
or minimum of the utilities among the applications for ``fair''
sharing.
MRMD Problem: For a given set of tasks 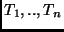 ,
our problem is to assign qualities ( ,
our problem is to assign qualities (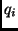 )
and allocate resources from various resource units (or, containers)
( )
and allocate resources from various resource units (or, containers)
( )
such as processors or network links to tasks or applications, such
that the system utility )
such as processors or network links to tasks or applications, such
that the system utility 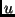 is maximized. In other words, what we have is the following:
is maximized. In other words, what we have is the following:
maximize
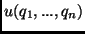
subject to
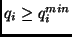 or
or
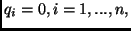 (QoS Constraints)
(QoS Constraints)
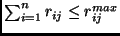 , ,
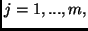 (Resource Constraints)
(Resource Constraints)
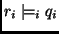
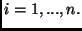
A task is made fault-tolerance through its replication. A replica
will run on different set of resources with respect to. the
original at the same quality level. The number of replicas that need
to be run depends on the fault model of the system. Hence, following
a certain fault-model, we can assign fault-tolerance as another QoS
dimension. The values along this dimension is equated to the number
of copies (replicas) of the task. The utilities achieved depend on
the fault-model or the reliability of the system.
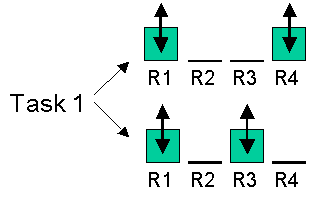
For example, consider a task  that has the following resource vector allocation choices (options):
that has the following resource vector allocation choices (options):
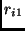 , ,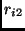 and
and 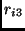 .
At the same level of quality, any of these resource choices can be
allocated to the task. In order for the task to be fault-tolerant,
more than one resource vectors need to be allocated. Thus, we can
generate the QoS set-points in the following way: .
At the same level of quality, any of these resource choices can be
allocated to the task. In order for the task to be fault-tolerant,
more than one resource vectors need to be allocated. Thus, we can
generate the QoS set-points in the following way:
| Fault-tolerance
Quality Index |
Number
of replicas |
Resource
Vectors |
| 1 |
0 |
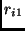 , ,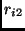 , ,
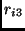 |
| 2 |
1 |
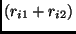 , ,
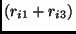 , ,
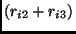 |
| 3 |
2 |
 |
For a task with 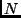 resource vector options, the fault-tolerant quality index of
resource vector options, the fault-tolerant quality index of 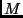 can be attained in
can be attained in
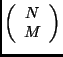 combinations of resource vectors. This automatically limits the
maximum number of replicas to the number of independent
resource options.
combinations of resource vectors. This automatically limits the
maximum number of replicas to the number of independent
resource options.
Resource
Allocation Algorithm
The algorithm can be summarized as follows:
Pre-processing
 |
Using
the user and application profiles generate the
resource/utility curves for each task |
 |
Apply
convex hull algorithm to eliminate non-performing
set-points |
Optimization
 |
Initialize
all tasks to their minimum QoS level. |
 |
Compute
the marginal utility (Dutility/Dresource)
each task can receive by increasing QoS by one
step |
 |
Choose
the task with the highest marginal utility and increase it's
QoS by one step. If unallocated resources remain, go back to
step 2. |
 |
Stop
when no more resources can be allocated. |
Multi-Resource
QoS Optimization
Multiple resources in Q-RAM are handled by computing a
"composite resource". The algorithm is executed using
composite resource as the comparison metric. The composite resource
is obtained from the formula:

Where 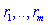 are the different
components of a resource vector and are the different
components of a resource vector and 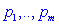 is the penalty vector depicting the relative demands of resources of
each type.
is the penalty vector depicting the relative demands of resources of
each type.
Multi-resource
trade-off

A task may have a set of set-points for the same QoS/Utility
level and "composite resource" may not accurately differentiate
between those set-points. The solution approaches are the
following:
 |
Apply
Q-RAM to each combination of resource options over all tasks
(exhaustive search). This has exponential complexity with respect to
the number of tasks. |
 |
Random
selection of option for each task |
 |
"Intelligent"
pre-selection of options for each task |
 |
Refinement
of the Amrmd algorithm to accommodate option refinement. |
More information, take a look at the paper here.
Hierarchical
Q-RAM: Scalable Resource Allocation of Large Systems
The basic
resource allocation algorithm for a large distributed system with
large number of tasks and resources has scalability problems. Hence
it has been extended to hierarchical version. The main ideas are the
following:
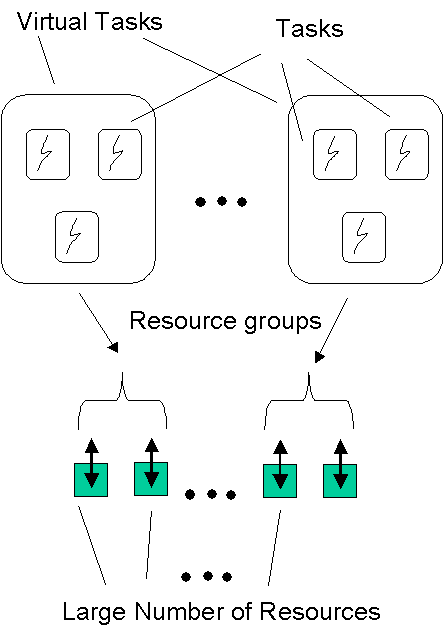
Divide the task into groups or "virtual tasks"
Derive approximate utility functions for the virtual tasks
corresponding to the groups Perform "Amrmd" globally on
each virtual tasks to determine their near-optimal resource
allocations Multiple levels hierarchies thus can be formed. |