 |
Nicholas Roy
One essential component of any operational mobile robot system is the ability for the robot to localize itself; that is, to determine its position in space consistently and accurately from sensor data. There are many successful localization methods that are able to determine a robot's position relative to a map using sonar, laser and camera data.
However, most localization methods fail under common environmental conditions. For example, localization error can arise when a mobile robot follows a path through a wide-open space, such as outdoors, or in a very large or crowded room. Cameras can also fail in regions which lack sufficient visual structure, such as blank walls or ceilings. Since these environmental conditions are relatively common, a mobile robot navigating reliably in the real world must allow for the potential failure of its localization methods.
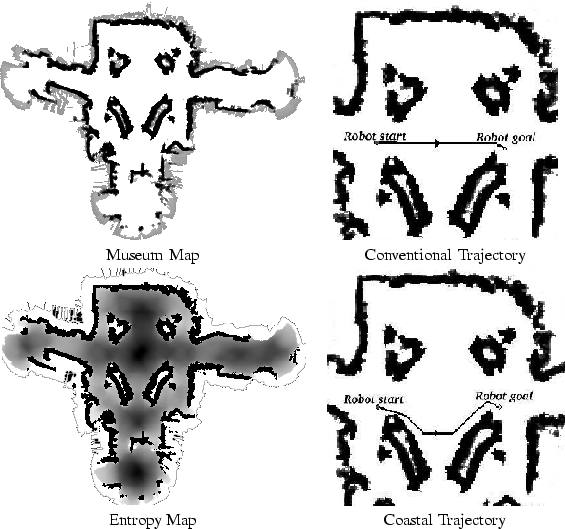
The motivation for coastal navigation is generating trajectories for the mobile robot that reduce the likelihood of localization error. Our solution is to have the robot identify how good regions of space are for localization, and alter the path planning accordingly. We have developed a planner that uses maps of the environment, where each cell in the map contains a notion of information content available at that point in the map, that corresponds to the ability of the robot to localize itself. The higher the information content, the better the localization ability.
Developing motion planning algorithms based on positional uncertainty is not a new idea. Erdmann developed such strategies as well as probabilistic strategies. Work has been done on trajectory generation with respect to positional uncertainty. Takeda et al. [Takeda et al., 1994] do not use the localization process to generate the positional uncertainty across space, but generate probability distributions based on an explicit model of the sensor, and therefore is not generalizable across sensors. Furthermore, the environment is assumed to be static, so the effect of dynamic obstacles on localization is not modelled.
Considerable work in the field of partially observable Markov decision processes (POMDPs) [Koenig and Simmons, 1996] has allowed many mobile robots to model positional uncertainty explicitly. The POMDP process is in fact mathematically elegant solution; a POMDP produces a policy for all states in the environment and can therefore be used to produce the optimal policy for any desired goal location and uncertainty state, assuming such a policy exists. However, one drawback to the use of traditional POMDPs is that the computation time is exponential in the number of states. In a real-world environment, POMDPs are completely computationally intractable. Essentially our solution operates by reducing the high-dimensionality of the POMDP to two or three dimensions, allowing the use of a dynamic programming approach to find the policy for the low-dimensioned space.
Our solution to these problems is inspired by traditional navigation of ships. Ships often use the coasts of continents for navigation in the absence of better tools such as GPS, since being close to the land allows sailors to determine with high accuracy where they are. The success of this method results from coast lines containing enough information in their structure for accurate localization. By navigating sufficiently close to areas of the map that have high information content, the likelihood of getting lost can be minimized.
 |
We have developed a measure of the information content of the environment
based on the results of the localization process. Let the robot's position be
given by the initial probability distribution,
![]() ,
defined over
,
defined over
![]() .
The robot acquires a sensor measurement
.
The robot acquires a sensor measurement ![]() ,
for example a set of range data from a laser sensor. The localization process
takes
,
for example a set of range data from a laser sensor. The localization process
takes
![]() and the sensor data,
and the sensor data, ![]() ,
and returns the posterior
probability distribution
,
and returns the posterior
probability distribution
![]() ,
again defined over the space of poses of the robot,
,
again defined over the space of poses of the robot,
![]() .
.
The entropy,
![]() ,
of a probability function,
,
of a probability function,
![]() ,
provides a good measure of the certainty with which the robot is localized.
The entropy of a probability distribution,
,
provides a good measure of the certainty with which the robot is localized.
The entropy of a probability distribution,
![]() ,
is computed over the
space of all possible poses
,
is computed over the
space of all possible poses
![]() and is defined as:
and is defined as:
For a particular pose distribution, we can compute the information content,
I, of the robot's current position by computing the difference between the
expected entropy of the positional probability conditioned on the sensor
measurement,
![]() and the entropy of the prior
position distribution,
and the entropy of the prior
position distribution,
![]() :
:
We have ignored the issue of the prior probability distribution of the robot's
position. The entropy computation is heavily dependent on the robot's prior
belief in its position,
![]() .
Modeling robot navigation as a partially
observable Markov decision process, or POMDP, would be one method for handling
this dependency [Kaelbling et al., 1998]. However, the POMDP requires examining all
possible prior probability beliefs and also all possible paths leading up to
the prior probability belief. This process provides an extremely accurate
characterization of uncertainty, however, for planning, the computation is
intractable, as it is exponential in the size of the environment. We have
therefore made some simplifying assumptions in the implementation of the
algorithm which dramatically reduce the complexity. One such simplification
allows us to ignore the problem of the prior positional distribution.
.
Modeling robot navigation as a partially
observable Markov decision process, or POMDP, would be one method for handling
this dependency [Kaelbling et al., 1998]. However, the POMDP requires examining all
possible prior probability beliefs and also all possible paths leading up to
the prior probability belief. This process provides an extremely accurate
characterization of uncertainty, however, for planning, the computation is
intractable, as it is exponential in the size of the environment. We have
therefore made some simplifying assumptions in the implementation of the
algorithm which dramatically reduce the complexity. One such simplification
allows us to ignore the problem of the prior positional distribution.
Figure 1 shows an example map on the left of the Smithsonian Museum of American History, and the information content of the same museum on the right. In the information content map, the darker an area is, the less information it contains. Notice that the darkest area is the center of the large open space in the middle, and that the lightest areas, with the lowest entropy are close to the walls.
One avenue for future research lies in the path planner. The dynamic programming technique currently used for finding the minimum-cost trajectories demands a monotonic integration of the entropy. Therefore, there is no way to model actions that reduce uncertainty. Extending the planner to model uncertainty explicitly as a third state rather than including the information content in the cost function given to the planner would allow more formal modeling of the uncertainty and the application of this work to other domains. In particular, the current approach cannot be used for such traditional planning problems as mail delivery or scheduling.