Active Learning in Mobile Robots
David Cohn
When operating in a new environment or performing a new task, a robot
may require an enormous amount of data, in the form of experience,
before it can perform adequately. It may need to calibrate its models
of
- sensing:

- acting:

- deciding:
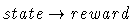
Uncertainty and inaccuracy in any of the models will hamper a robot's
performance. As it continues to operate, it will be able to use data
from its experiences to improve its models and reduce future
loss. When the environment is large or complex, however, gathering
sufficient data by random exploration (or by simply trying to perform
the task at hand) may require an inordinate amount of time and wasted
effort.
But what if the robot were allowed to explore its domain, to
explicitly take actions that it thinks will improve its model of the
world, and hence its ability to perform the assigned task? What
actions should it take? This is the question addressed in the study
of ``active learning.''
Theoretical limits on the benefits of active learning are hard to come
by, but empirically, the accuracy of maps and predictions can be
increased by orders of magnitude over those based on data gathered at
random. The difference is most pronounced in domains that have state -
where the learner's exploration must follow a trajectory through the
space. This type of domain is pervasive in robotics. Here, random
exploration results in thrashing and an uninformative ``drunkard's walk.''
Prior work in active learning has fallen primarily into two
camps. Statisticians have employed techniques related to active
learning for many years now, but most of that work is restricted to linear
models, and is non-adaptive - the ``best'' set of actions to take is
estimated at the beginning of the exploration process, and is not
re-evaluated as intermediate results are observed.
Work that does consider adaptive exploration on more complex
models (such as neural networks and other machine learning
architectures) has generally relied on heuristics such as exploring areas
where we have the least data, or where the model has made errors in
the past. By ignoring the underlying statistics and the interaction
between the data and the model to which it is being applied, these
approaches often result in haphazard, inefficient exploration.
Active learning poses a number of challenges. First, one must
efficiently estimate both the loss resulting from inadequacies in the
current model, and the expected effect that an arbitrary action will
have on those inadequacies. One must then optimize, finding an
acceptable action that results in minimum expected posterior loss.
The key insight of our approach is that of making explicit use of the
statistical nature of machine learning. We use simple statistical
models for our representations, such as mixtures of Gaussians and
locally weighted regression. These representations allow fast, closed
form evaluation of conditional means, variances and their gradients,
as well as recursive updates to those quantities.
Armed with an efficient method of computing conditional means and
variances, we can use bootstrap and related sampling techniques to
estimate model loss. The differentiable nature of the models means we
then have access to a loss gradient, and can choose between Monte
Carlo and hillclimbing methods for optimization. Such computationally
intensive would be unmanageable with a less parsimonious model in the
inner loop.
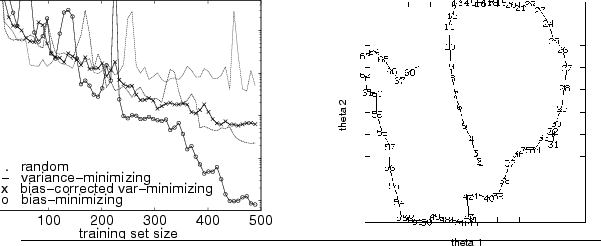
Figure 1:
Kinematic exploration for a toy two-joint robot arm. (left)
MSE as a function of number of noisy exploration steps for random
exploration and optimal exploration under various statistical
assumptions. Computing and exploring along an optimal trajectory is
several orders of magnitude more efficient than random
exploration. (right) Sample exploration trajectory, exploring to
minimize integrated squared error of the learner's model.
 |
In many situations, a robot cannot take time off from performing a
task and explore its environment to build a better model of it. In
this case, it must make the classic exploration-exploitation
tradeoff, weighing an action both by how well it helps the robot
achieve its immediate goal, and by how much it will improve the model to boost performance on future goals. In general,
computing this tradeoff exactly is intractable. Closed form
approximations to the tradeoff, however, would greatly expand the range
of problems to which active exploration could be applied.
Another shortcoming of the current approach is that it is greedy - it
only considers the next action the robot is to take. Preliminary
results indicate that in some domains there is much to be gained by
planning an optimal sequence of actions and adapting the plan as
results of intermediate actions become known. The present algorithm,
however, is not fast enough to optimize and adapt a sequence of
actions in a reasonable amount of time - some tractable, yet
statistically sound, approximation must be identified.
- 1
-
David Cohn.
Neural network exploration using optimal experiment design.
Neural Networks, 9(6):1071-1083, 1996.
- 2
-
David Cohn.
Minimizing statistical bias with queries.
In M. Mozer et al., editor, Advances in Neural Information
Processing Systems 9, Cambridge, MA, 1997. MIT Press.
- 3
-
David Cohn, Zoubin Ghahramani, and Michael Jordan.
Active learning with statistical models.
Journal of Artificial Intelligence Research, 4:129-145, 1996.
This document was generated using the
LaTeX2HTML translator Version 98.1p1 release (March 2nd, 1998).
The translation was performed on 1999-02-27.
