Fast Algorithms for All-Point-Pairs Learning Problems

Alexander G. Gray and Andrew W. Moore

Problem:

There is a large class of common statistical problems, which we call all-point-pairs problems, or 'N-body'-like problems. These are problems which abstractly require a comparison of each of the N points in a dataset with each other point and would naively be solved using N² distance computations. Such algorithms cannot be applied to practical problems where N is large.

The N-body problem of computational physics and the all-nearest-neighbors problem of computational geometry can be considered part of this class. In this work we focus on six examples of all-point-pairs problems within statistical learning: nearest-neighbor classification, kernel density estimation, outlier detection, the two-point correlation, the multiple two-point correlation, and the n-point correlation.

The last two of these are actually examples of important generalizations beyond the standard all-point-pairs problems, which are more difficult. In particular the n-point correlation is an example of an n-tuple N-body problem. It is naively an O(Nⁿ) computation and thus has previously been considered computationally intractable for useful scientific analysis.

Impact:

The contributions of this work include the identification of this class of computational problems in statistics, six very fast algorithms illustrating our exploitation of geometry in statistics, and more importantly a suite of geometric techniques forming a framework for designing algorithms for any N-body problem. The last of our examples, the n-point correlation, illustrates a generalization from all-point-pairs problems to all-n-tuples problems, which are much harder (naively O(Nⁿ)). For all the examples, we believe there exist no exact algorithms which are faster either empirically or theoretically, nor any approximate algorithms that are faster while providing guarantees of acceptably high accuracy (as ours do). For n-tuple N-body problems in particular, this type of algorithm design appears to have surpassed the existing computational barriers, providing the first method that can practically compute the n-point correlation. In addition, all the algorithms in this paper can be compactly defined and are easy to implement.

We show that, for uniform data (a pessimistic case), our algorithms exhibit favorable asymptotic scaling. Empirically we also show that these methods yield several orders of magnitude in speedup over the naive computation, even for medium-sized datasets. In addition, all the algorithms presented are surprisingly easy to describe and implement.

State of the Art:

Currently, with a few exceptions noted below, we are aware of no exact approaches to nearest-neighbor classification, kernel density estimation, outlier detection, the two-point correlation, or the n-point correlation having running time better than O(N²). However, in some cases ad hoc methods have been proposed which yield approximations to the desired computation. All these algorithms, to our knowledge, are impractical or for other reasons have not found widespread acceptance. One of the exceptions is an algorithm proposed by one of the authors [2] achieves 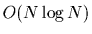$O(N\log N)$ performance for nearest neighbor classification using an approach similar to that described here. For the two-point correlation, 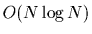$O(N\log N)$ approximate algorithms based on simple gridding and binning methods have found widespread use but are generally too approximate for scientific use. As stated earlier, no practical algorithms exist at all for the 3-point correlation and higher, even for small datasets.

Approach:

The key to our fast solution of these problems is the exploitation of the hyperstructure of a data space, i.e. the geometric structure of the dataset within its multivariate feature space. Our specific instance of this idea in this paper is to 1) precompute a data structure which defines a geometric partitioning of the space, and 2) use this data structure within the algorithm to perform geometric reasoning allowing entire chunks of the data to be considered at once in the computation. The algorithm may choose to ignore a chunk of data, include its entirety in the computation's answer, penetrate it further, or approximate it (see below) as appropriate.

A second essential idea forming the basis of our approach is that of cached sufficient statistics [1]. The main observation is that one can precompute some sufficient statistics, as appropriate to the computation, and store these in our data structure. The instant availability of these statistics is what allows us, in many cases, to approximate a chunk of data. In the algorithms in which we approximate, we can make our computation arbitrarily close to the precise one, at the cost of efficiency.

Our methods use dual Multiresolution KD-trees, one for each of the two sets of points, performing node-node comparisons rather than the previously used point-node comparisons with a single KD-tree [2]. This is a fundamental advance over the previous methods, which is natural in our current setting in which the query set Q is known in advance. We then have the opportunity to analyze its hyperstructure as well as that of the dataset D, building a separate KD-tree for Q in addition to the one built for D.

Future Work:

Finally, besides addressing a large number of problems in nonparametric statistics, the algorithmic framework presented can be applied in principle to a broad array of other machine learning methods, for very fast learning of, for example, large-scale radial basis function neural networks, mixtures of Gaussians, and hidden Markov models.

References:

[1] Andrew W. Moore and Mary Soon Lee. Cached Sufficient Statistics for Efficient Machine Learning with Large Datasets. Journal of Artificial Intelligence Research, Vol. 8, 1998.

[2] Kan Deng and Andrew W. Moore. Multiresolution Instance-Based Learning. Proceedings of the International Joint Conference on Artificial Intelligence (IJCAI), 1995.

[3] Alexander G. Gray and Andrew W. Moore. 'N-Body' Problems in Statistical Learning. Advances in Neural Information Processing Systems 13 (Submitted May 2000, Proceedings published May 2001).

About this document ...

Fast Algorithms for All-Point-Pairs Learning Problems

This document was generated using the LaTeX2HTML translator Version 98.1p1 release (March 2nd, 1998)

The command line arguments were:
latex2html -debug -white -no_fork -no_navigation -address -split 0 -dir html -external_file alex alex.tex.

The translation was initiated by Daniel Nikovski on 2001-01-23