

Next: LOCALLY DEFINED QUASI-BAYESIAN NETWORKS
Up: QUASI-BAYESIAN THEORY
Previous: Conditionalization
There is no unique way to define independence relations with credal sets;
in the most in-depth study of this matter, Campos and Moral have reviewed
five different possible types of independence [10].
The results presented in this paper adopt Walley's definition of
independence [28]. Walley's original definition was stated in terms
of lower expectations; to develop a theory of convex sets of distributions,
it is important to recast Walley's definition using credal sets as follows.
Consider sets of variables 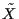 ,
,
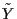 and
and 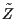 and the credal sets
and the credal sets
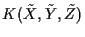 ,
,
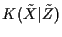 ,
,
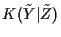 ,
,
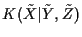 and
and
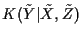 .
Note that distributions
in
.
Note that distributions
in
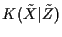 and
and
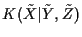 are
defined over the same algebra of events
once
are
defined over the same algebra of events
once 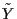 and
and 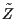 are fixed; likewise, distributions
in
are fixed; likewise, distributions
in
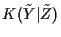 and
and
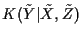 are defined over the same algebra of events once
are defined over the same algebra of events once 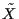 and
and 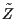 are fixed.
are fixed.
Definition 1
Variables
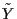
are
irrelevant to
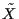
given
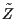
if
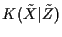
is equal to
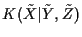
regardless of the value of
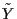
,
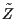
.
Variables
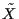
and
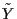
are
independent given
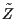
if
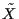
is
irrelevant to
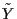
given
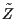
and
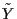
is irrelevant
to
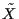
given
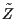
.
If
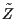
is empty, suppress the
``given
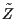
'' from this definition.
This concept of independence does not imply that joint credal sets
contain only joint distributions with independent marginals, nor does
it imply uniqueness for the joint credal set [28, Chapter 9].


Next: LOCALLY DEFINED QUASI-BAYESIAN NETWORKS
Up: QUASI-BAYESIAN THEORY
Previous: Conditionalization
Fabio Gagliardi Cozman
1998-07-03
![]() ,
,
![]() and
and ![]() and the credal sets
and the credal sets
![]() ,
,
![]() ,
,
![]() ,
,
![]() and
and
![]() .
Note that distributions
in
.
Note that distributions
in
![]() and
and
![]() are
defined over the same algebra of events
once
are
defined over the same algebra of events
once ![]() and
and ![]() are fixed; likewise, distributions
in
are fixed; likewise, distributions
in
![]() and
and
![]() are defined over the same algebra of events once
are defined over the same algebra of events once ![]() and
and ![]() are fixed.
are fixed.