

Next: Conditionalization
Up: QUASI-BAYESIAN THEORY
Previous: Credal sets
Given a convex set K of probability distributions, a probability
interval can be created for every event A by defining lower and upper bounds:
Lower and upper expectations for a function f(X) are defined as
(Ep[f] is the expectation of the function f):
There is a one-to-one correspondence between lower (or upper)
expectations and credal sets. Given a credal set, the set of all
lower expectations for all arbitrary functions f(X) is unique,
and vice-versa.
Fabio Gagliardi Cozman
1998-07-03
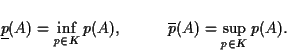
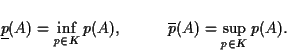
![\begin{displaymath}
\underline{E}[f] = \inf_{p \in K} E_p[f],
\hspace{1cm}
\overline{E}[f] = \sup_{p \in K} E_p[f].
\end{displaymath}](img8.gif)