Mike Schuresko, Assignment 3 (IBMR)

I used an algorithm that was markedly different from the one presented in class, I was able (with a limited degree of success) to extract 3d information from a user tracing the outlines of what would be rectangles in 3d. A sample screen-shot is shown.

extract camera parameters
for each rectangle
- project rays in 3d
- reproject onto plane perpendicular to rectangle centroid.
- recognize that diagonals of a rectangle are bisectors of each-other
- scale all vectors appropriately so that the following relationships can be used.
  
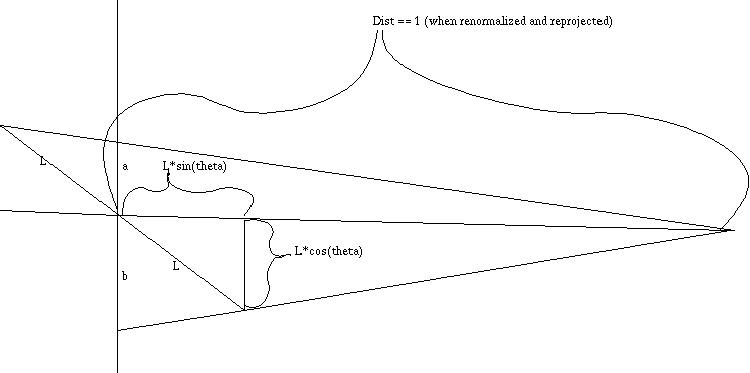
  yielding,
  - l*sin(theta) = (a-b)/(a+b)
    and
  - l*cos(theta) = b*(1+l*sin(theta))
  the other angle neccessary to determine the 3d orientation of the rectangle's diagonal can be obtained straight from the reprojected image
Extract distance to rectangle via the following procedure
- user inputs the distance to one object in scene
  this is actually quite arbitrary, this object merely determines the scale, not the geometry, of the model
- for all other rectangles, user selects a point that intersects the plane of another rectangle, draws an arrow between them.

right and middle mouse buttons for zoom
left mouse button for moving image and adjusting points
- click on rectangle centroid to translate rectangle
- click on rectangle corner to adjust that corner
- shift-click on rectangle edge to draw arrows indicating planar intersections
- double click on one rectangle centroid to specify absolute distance.
rectangle centroids always displayed
depth-dependency from planar intersections forms a tree rooted at the rectangle whose depth the user specifies by hand.
Algorithm finds depth by searching up from a leaf and memoizing results.

Somewhat unstable algorithm, unsuitable for real-world data.
Because this algorithm doesn't make any assumptions about the relative angles of the rectangle planes, often scenes that have very strong right angles show up very badly in 3d-models. My method does not take advantage of the data redundancy that other single-view metrology algorithms use
Actual algorithmic flaw in computing camera parameters.
I use parrallel lines on rectangles to compute the camera depth, but I have no method to extract the center of projection. I currently assume its at the center of the image. Some of the models I attempted (most notably, Albrecht Durer's "St Jerome in his study") had a center of projection other then the center of the image.

Future Work
- have a "3d-edit" mode where users can drag points in 3d to correct for obvious mistakes from the algorithm
- find some method for calculating eye-center-of-projection (possibly by numerically minimizing entropy in the camera-depth computation)
- integrate with an "image-based teddy" so that architectural and organic elements can be modeled toghether.
Sample results
- decent results
- flawed results
  - Sears Tower
    problem likely due to algorithm instability
  - St Jerome in his study
    problem likely related to center of projection
  - Screenshot from creating "St Jerome in his study"
  - National Cathedral Inside
    problem likely due to numerical instability
Michael D Schuresko
Last modified: Fri Nov 5 16:26:25 EST 1999