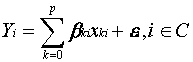 (4.1)
(4.1)
Spatial Analysis of Crime Using GIS-Based Data: Weighted Spatial Adaptive Filtering and Chaotic Cellular Forecasting with Applications to Street Level Drug Markets
A dissertation submitted to the
H. John Heinz III School of Public Policy and Management,
Carnegie Mellon University
in partial fulfillment of the requirements
for the degree of Doctor of Philosophy
by
Andreas M. Olligschlaeger (olli@cs.cmu.edu)
May, 1997
Acknowledgments
Numerous people contributed to the various projects which this dissertation is based on. First and foremost I would like to thank my dissertation committee: Wil Gorr, Jackie Cohen and Ramaya Krishnan for their support and thoughts as the dissertation progressed. Wil and Jackie especially spent endless hours with me going over results and hashing out details, and they are directly responsible for bringing me in on the DMAP project which started this whole thing. However, when it comes to service above and beyond the call of duty, Wil Gorr stands out. In my 17 (!) year career as a full time student at three universities I have never met a professor more dedicated to his work and his students than Wil. I consider myself extremely lucky to have been his student and I am a better person for it.
I would also like to thank the folks at the National Institute of Justice, especially Craig Uchida and Nancy LaVigne for supporting my research over the years, as well as some of the other DMAP researchers, including Lorraine Green-Mazerolle, David Weisburd and Tom McEwen for their invaluable input. In addition, I would to thank my "moral support team", consisting of one former NIJ researcher, one geographer, and numerous beers at a New York City Irish pub to help me get through the final phase of this dissertation.
Finally, I would like to thank all of the dedicated folks in the City of Pittsburgh, including Chief Earl Buford, Commander Bill Bochter and Sgt. Mona Wallace of the Pittsburgh Bureau of Police, as well as Darrell Packer, Glen Bigler and Ed Wells for their support on the DMAP project.
Abstract
With the recent emphasis towards proactive Community Oriented Policing and the increase in the use of computerized information systems for data collection police departments are faced with two major problems: (1) how to mine the vast amounts of data produced by these systems, and (2) how to use this data to provide information that supports proactive law enforcement.
This dissertation makes a contribution in this area by providing the model specification and framework for such tools, a GIS-based data collection system, and a new spatio-temporal forecasting method - chaotic cellular forecasting (CCF) - for use by an early warning system for emerging drug markets.
Table of Contents
1. Introduction
2. Data Sources and Data Collection Methodology
2.1 Introduction
2.2 The Pittsburgh DMAP Program
2.3 Geobase Files
2.4 Data Sources
2.4.1 Call For Service Data
2.4.2 Police Records Data
2.4.3 Property Ownership Data
2.5 Geocoding Methodology
2. 6 Data Collection and Aggregation
2.7 Conclusion
3. Modeling Street-Level Illicit Drug Markets
3.1 Introduction
3.2 Drug Enforcement
3.3 Literature on the Ecology of Crime
3.4 Model Specification and Data
3.5 Modeling Results
3.6 Conclusion
4: Weighted Spatial Adaptive Filtering: Monte Carlo Studies and Application to Illicit Drug Market Modeling.
4.1 Introduction
4.2 Varying Parameter Models and Methods.
4.3 Spatial Adaptive Filter
4.4 Multiple Feedback Pattern Recognizer
4.5 Monte Carlo Study
4.6 Monte Carlo Results
4. 7 Case Study
4.8 Conclusion
5. Chaos Theory, Artificial Neural Networks and GIS-Based Data: Chaotic Cellular Forecasting and Application to the Prediction of Drug Related Call for Service Data
5.1 Introduction
5.2 Spatial Forecasting Methods and Models
5.3 Chaotic Cellular Forecasting
5.4 Forecasting Drug Calls for Service: A Comparison Between Traditional Forecasting Methods and Chaotic Cellular Forecasting
5.5 Conclusion
6. Summary and Conclusion
7. Literature Cited
Appendix A
1. Geocoded Data Files Accessed Directly By DMAP
2. PSMS Data Files Indirectly Accessed by DMAP
Appendix B
Appendix C
Figure 4.4
Figure 4.5
Figure 4.6
Figure 4.7
As police organizations automate their operations and implement more modern computer systems, taking advantage of advances in information technology such as open architecture database systems, enterprise wide computer applications and ever increasing microprocessor and network speeds, more and more information will become available to police officers at the click of a mouse button. Moreover, all of this information will be linked together from various sources and organized in ways which were previously unheard of. Police investigators will likely find this wealth of information a boon to their work, but crime analysts and police administrators may well find themselves faced with information overload.
At the same time that police departments are making increasing use of computer technology they are also undergoing a change in law enforcement philosophy. Evidence of this change can be seen in the fact that many police departments are implementing Community Oriented Policing (C.O.P.) in an effort to emphasize proactive rather than reactive law enforcement. While the concept of Community Oriented Policing is certainly not new (for a review of early C.O.P. initiatives see Trojanowicz, 1986) the way in which information is utilized in Community Oriented Policing has changed over the years. In many cities desktop personal computers have replaced the daily log for foot patrol officers and in some cities the time honored tradition of a notebook and pencil has given way to hand held, pen based mobile computers.
An abundance of tools and methodologies have been developed that support traditional reactive law enforcement. Practical examples include investigative tools such as linkage analysis, geographic offender profiling and modus operandi systems. Geographic information systems have also played a large role, both from a practical and a research perspective. Research examples include measuring the geographic displacement of drug offenders (Green, 1993), monitoring the effects of law enforcement strategies on nuisance bar activity (Cohen et al., 1993) and point pattern analysis of crime locations (Canter, 1993). Other examples of more general purpose crime mapping systems for law enforcement include the Drug Market Analysis Program (DMAP) effort undertaken in Jersey City, Hartford, San Diego, Pittsburgh and Kansas City (McEwen and Taxman, 1994; Maltz, 1993) and PA-LEGIS (Pennsylvania Law Enforcement Geographic Information System), an integrated GIS and police records management system developed for smaller police departments (Bookser, 1991).
There is no doubt that tools for reactive policing will always play an important role in law enforcement. However, proactive law enforcement will require an entirely new set of tools, the development of which has only just begun. Proactive problem solving by detectives, community oriented police officers and police officials not only requires access to up-to-date information on criminal activity, but perhaps more importantly the ability to anticipate emerging crime trends. This in turn requires the ability to mine the vast amounts of data produced on a daily basis by 911 and police record management systems, police hot line tips and citizen complaints for signs of impending flare-ups, geographic displacement or other unusual criminal activity. In other words, proactive law enforcement needs tools that can anticipate or provide early warning of criminal patterns so that they may be prevented.
This dissertation makes a contribution in this area by providing the model specification and framework, a GIS-based data collection system, and a new spatio-temporal forecasting method - chaotic cellular forecasting (CCF) - for use by an early warning system for emerging drug markets.
The second chapter focuses on the development of a geographic information system that provides the underlying data for the dissertation. This practical application of GIS to narcotics enforcement arose out of the Drug Market Analysis Program (DMAP) funded by the National Institute of Justice (NIJ). A by-product of the DMAP program was a very accurate data set consisting of point (i.e., address) level data on illicit drug market activity and related crimes.
Chapter 3 is a study employing multiple regression techniques to analyze the effects of both traditional and ecological variables on illicit drug markets. The study was in part made possible due to the fact that DMAP includes high quality location data on ecological variables such as land use and the built environment.
Chapter 4 is an empirical study introducing weighted spatial adaptive filtering which provides evidence that spatial interaction, local context and spatially varying model parameters are important indicators of street level drug dealing.
The fifth chapter introduces chaotic cellular forecasting. CCF employs the findings of the previous chapters and combines chaos theory, artificial neural networks (ANN's) and grid cell aggregated GIS-based data to produce one-step-ahead forecasts of street level drug market activity. One of the underlying assumptions of CCF is that spatio-temporal patterns of criminal activity can be modeled as a chaotic system. Artificial neural networks, more specifically feedforward networks with backpropagation, are then used to estimate the forecasting model. Backpropagation models are uniquely qualified for this purpose because they are self adapting and are universal approximators (Hornik et al., 1989). Two versions of CCF, one using spatially constant weights (analogous to spatial regression using spatially constant parameters) and the other a hybrid model of spatially varying input to hidden unit weights and constant hidden to output units weights are tested. The results are compared to both a simple and a state-of-the art spatial regression model using spatially lagged variables and tested for forecast accuracy on a holdout data sample.
The sixth and final chapter provides a summary and outlines future work.
2. Data Sources and Data Collection Methodology
Over the past five years GIS has become a standard tool for crime analysts in many police departments, regardless of their size (see for example McEwen and Taxman 1994; Rossmo, 1995). One of the inherent advantages of GIS is its ability to integrate information from a variety of sources into one user interface. In turn, this allows for spatial analyses that would either not have been possible or at a minimum far more difficult prior to the advent of GIS.
One such GIS - the Pittsburgh Drug Market Analysis Program (DMAP) - is the primary source of data for this dissertation. DMAP was developed for the Pittsburgh Bureau of Police under a grant from the National Institute of Justice (NIJ - Grant #90-IJ-CX-007). DMAP was one of the first attempts to integrate GIS and a variety of law enforcement and public sources of data into one user interface and make it available to police officers. DMAP has been in daily use in the Pittsburgh Bureau of Police for the past five years and, while originally intended primarily for narcotics enforcement, has since been expanded to a general map-based crime analysis system.
From a research perspective DMAP has proved to be a rich source of data. One of the main advantages of an integrated GIS is that all data have one common denominator: the xy coordinates. Thus all data points can be related to others via coordinates or the address as well as other characteristics such as the date and time. This in turn allows for the aggregation of data over any desirable spatial and temporal unit, whether census tracts by year, municipal boundaries by month, or any user defined area by time of day. Without this capability most of this dissertation would certainly not have been possible.
This chapter of the dissertation discusses the development of DMAP as well as some of the problems encountered in integrating and aggregating data from a variety of incompatible sources. Towards that end the second section discusses the DMAP project, followed by a description of the various files in the third section. The fourth section outlines the non-geobase sources of data and discusses their limitations. Section five describes what was perhaps the largest hurdle in developing DMAP, namely how to ensure that data from various incompatible sources can be geocoded. Section six discusses how the data for this dissertation were aggregated. Finally, section seven summarizes the chapter.
2.2 The Pittsburgh DMAP Program
In the summer of 1990 the City of Pittsburgh was one of five cities (the others were Hartford, Kansas City, Jersey City and San Diego) awarded grants from the National Institute of Justice to develop new technologies for police and to evaluate the effectiveness of law enforcement strategies aimed at curbing illicit street level drug trafficking. As most other cities participating in the grant, Pittsburgh chose to develop a GIS for use by narcotics officers to track drug related information from a variety of sources. More specifically, DMAP allowed narcotics officers and administration officials to query data from multiple sources according to a number of geographic criteria. The results of the queries were displayed as maps which showed point information about certain crimes or calls for service (911 data). This point information could then be further queried for more detailed reports and descriptions of drug and other criminal activity. DMAP was implemented in 1991 and has been in use on a daily basis since.
While the original goal of DMAP was to design and implement a GIS-based system targeted specifically for narcotics enforcement, it was quickly realized that the system would also be useful in other areas of law enforcement. As a result, the federal grant was extended by the City of Pittsburgh so that a more general crime analysis mapping system could be developed. This system went into its final production phase in the spring of 1996 and has been in daily use in the crime analysis division of the Pittsburgh Bureau of Police since, where in addition to using the system in investigations approximately 15 maps per week are produced to support law enforcement officials in their daily tasks. Today, after a total of five years of ongoing development and six years of operation, the DMAP system is comprised of approximately 45,000 lines of programming code (about 60% of which is written in C and the rest in AML) and contains over one gigabyte of data.
The development of DMAP required that a number of hurdles be overcome. Most geographic information systems in use today are still standalone systems, i.e., they are not integrated with other systems. Indeed, the tools required for full integration are only just now becoming commercially available to software developers. This made the task of integrating multiple sources of incompatible information more challenging. In addition, the Arc/Info software environment on which DMAP is based, in particular the database portion, has a number of limitations which will be outlined below. Perhaps the most daunting task, however, was the fact that a system such as DMAP had not yet been developed, either commercially or as part of a research project.
In its current version DMAP serves a number of purposes. First, it supports the investigation of crimes by providing highly detailed information at the address level. For example, a detective can query for an address and within seconds obtain a complete history of that address, including any arrests or police incidents, 911 calls for service made from that address, whether persons living at the address have been repeat victims or perpetrators of crime, as well as property tax and ownership information. Second, DMAP is used by law enforcement officials to measure the effects of policing efforts by measuring the geographic displacement of crime over time and space. These effects can be displayed wither via choropleth maps showing changes over areal units such as census tracts or patrol sectors, as well as pin maps showing criminal activity before and after police events. A third area in which DMAP has been used is in support of other law enforcement activities such as court presentations and aiding efforts to identify and close nuisance bars.
The geobase of a geographic information systems consists of those files which are necessary for mapping. Unlike ordinary databases geographic information systems store information in layers instead of tables (although GIS also stores and accesses data in tabular format to relate layer information to attributes). Thus the geobase of a geographic information systems is made up of layers of information. The main difference between a layer and a table is that a layer stores data geographically instead of in rows: each data object is associated with one or more geographical coordinates. There are three types of data objects which can be stored in layers: points (single coordinate), lines and polygons. Examples of each type of object include neighborhood boundaries (polygon), water lines (line) and radio towers (point). In addition, each object has attributes (such as the neighborhood name or the height of a radio tower) which are usually stored in related tables, although they can also be a part of the layer. Overlaying one or more types of layers on top of the other results in a map.
The layers of data that constitute the geobase in DMAP were derived from the Pittsburgh Allegheny Geographic Information System (PAGIS). PAGIS is the City of Pittsburgh's geographic information system used primarily in the departments of City Planning and Public Works. One of the advantages of PAGIS layers is that they are very accurate. The majority of PAGIS layers were derived from air photographs taken in 1986 and 1992. Cartographic information on the air photos was then commercially digitized and converted to GIS layers. What makes the layers so accurate is the fact that PAGIS's tolerance requirement for geographic accuracy is plus or minus five feet. In other words, all of the xy coordinates stored in the map layers can be no further than five feet from their true location. While from an engineering point of view this is not accurate at all, the tolerance is extremely accurate from a GIS perspective. This accuracy has proven very valuable for law enforcement. For example, one of DMAP's features is the ability to determine automatically how far a drug dealer was from a school during an observed drug transaction by measuring the distance between the address where the incident occurred and the property boundary of the closest school. Federal law provides for minimum sentencing guidelines for drug dealers arrested within 1000 feet of a school.
The specific layers included in DMAP are: streets outlines, property parcels, building footprints, neighborhood boundaries, 1980 and 1990 census tract boundaries, patrol sectors, police zone boundaries, fire zones, emergency response areas, water features, bridges, park features, cemeteries, major traffic arteries, undermined areas, and miscellaneous features such as parking lots, walls and helicopter landing pads.
As mentioned earlier one of the most unique features of the DMAP system is its ability to integrate data from a variety of incompatible sources. DMAP relies on three main external sources of information which are updated on a regular basis. These are 911 calls for service, police incident and arrest data, and property tax and ownership information (see Appendix A for a detailed description of files). In addition, DMAP contains data which is not updated as frequently, including the location of schools and playgrounds and the locations and ownership of liquor licenses.
911 call for service data is downloaded on a monthly basis from the City of Pittsburgh's emergency operations center computer system. The 911 system was implemented in 1989, and is rapidly approaching the end of its life expectancy. Indeed, the system is scheduled to be replaced with a more modern client-server based system in early 1998. The system consists of an AT&T miniframe computer running an Oracle database application. Due to the age of the system the amount of information the computer can store is limited to ten days worth. Every ten days the data is archived onto backup tapes. This means that historical data is not available on an on-line basis. DMAP is currently the only system in the City of Pittsburgh with which it is possible to query historical 911 data.
Each year the Emergency Operations Center (EOC) processes approximately 550,000 calls for service for a variety of nature codes. Since the DMAP system runs on a standalone workstation it would be impossible to download all calls for service. Thus DMAP obtains a subset of the data, including all Part I (major) crimes such as homicides, robberies and rapes, as well as a selected set of other crimes, including drugs, burglaries, assaults and vice. The number of data points added to the DMAP database each month is approximately 3,750. Each call for service includes the date, time, location, disposition and nature code of the incident.
The 911 data has a number of limitations which merit discussion. First, each call has only one nature code (type of call) associated with it. The actual nature code may differ from the one originally entered. For example, a person may call the 911 center saying that a person has been shot. The police, after arriving on the scene, may well find that the person shot is in fact dead. Rather than changing the nature code to that determined by the police, it is the policy of the Pittsburgh EOC to keep the original nature code. More modern 911 systems have two nature codes associated with each call: one for the caller's perception of the type of incident, and one for the actual type of incident which is determined by the responding unit (fire, police or EMS). Thus in Pittsburgh for some types of nature codes the 911 data reflects citizens' perception of incidents rather than their true nature.
A second problem with the Pittsburgh 911 data is that the disposition code is used inconsistently. Examples of dispositions used include that a report was written as a result of the call, the actors were gone an arrival, and that the call was unfounded. Unfortunately, due to policy changes in the operation of the 911 center, the way in which dispositions are used have changed over the years. For example, a disposition coded as "GOA", or gone on arrival, has a different meaning today than it did three years ago. This means that it is not possible to compare historical data in terms of the disposition of a call for service.
Finally, the 911 data includes both citizen and officer initiated calls for service. Each time either an officer or a citizen calls in an event, it is entered into the 911 system regardless of who called it in. Again, this is a policy issue that results in data limitations. Each time an officer writes a police report or makes an on-sight arrest he/she calls the 911 center via radio to obtain a CCR (Crime Code Reporting) number. Since the CCR number is automatically generated by the 911 system, the officer initiated call is entered into the system the same way it would if a citizen were to make a call. Thus no separation between is possible. However, estimates by 911 personnel indicate that approximately 10% of all drug calls for service are officer initiated.
Data on police offense and arrest reports are downloaded on a weekly basis from the Public Safety Management System (PSMS). PSMS was implemented in 1988 and, like the 911 system, is fast approaching the end of its life span and is scheduled to be replaced by the end of 1997 with an Oracle based client-server system. PSMS is a networked database application running on a Honeywell mainframe computer. Data are downloaded via tape and converted from a proprietary Honeywell format to standard ANSI Unix format.
As with the 911 data, DMAP receives a subset of all data points in PSMS. Unlike the 911 system, however, PSMS contains historical information and is not archived. Currently, there are approximately 8 million records in PSMS. The PSMS information contained in DMAP consists of eight data tables plus approximately nine code tables (detailed information on the data tables are also included in Appendix A; however, the code tables are too large to list in the appendix). The data tables include information on cases, offense reports, arrest reports, arrest codes, the locations of offenses and arrests, victim and offender identities, and the residences of victims and offenders. Each week approximately 400 new cases are added to the data set.
In developing DMAP, the problems associated with PSMS data were far more serious than those encountered with the 911 system. First, the data had to be converted from a networked to a relational database architecture. Second, the database used by the GIS software - INFO - is not a truly relational database and cannot handle one to many relationships, of which PSMS contains several. Thus it was necessary to write a custom database engine in C. DMAP's database engine not only had to store the information contained in PSMS, but also needed to interface with the map layers in the geobase as well as with INFO, since INFO stores all of the addresses associated with data points. The DMAP database currently contains over 1.5 million data points associated with approximately 350,000 individual incidents. Therefore, in order to process all of this data in a timely manner and to provide fast access, binary tree indexing routines also had to be written.
Each incident in PSMS is based on a Criminal Control Record (CCR) number. This number is generated by the 911 system and is assigned to every new police incident to initiate a new case. Cases can have several different types of reports associated with them, including offense reports (i.e., the report associated with the original incident), arrest reports and supplemental reports. Supplemental reports usually have no address associated with them because their primary function is to act as a description of an ongoing investigation (for example, a witness interview in a homicide case).
Apart from the logistical and technological difficulties encountered there were also problems associated with data quality. When the DMAP project was first started, 100 cases were randomly extracted from the files in the narcotics division and compared to the data found in PSMS. Approximately 55% of the cases had one or more errors in the corresponding PSMS data file (the error rate has since improved dramatically due to better data entry quality control). The most serious errors included listing persons that had nothing to do with the case as arrestees, listing victims as offenders, and omitting arrested persons altogether. These types of errors occurred in two or three percent of cases. The most common error was the omission of the address where an incident occurred (approximately 40% of all cases).
The majority of cases with missing addresses involved arrest reports. A subsequent analysis of the data as well as interviews with shift supervisors of the data entry section revealed that, while a part of the missing addresses were in fact due to omission (about 10% of the cases), most of them were not entered on all reports associated with a case because they were the same for all reports. For example, if a case involved three arrests, and all three arrests occurred at the same location as the offense report, then only the offense report would have an entry for an address. In practice this is true mainly for cases in which on on-sight arrest occurred. For most types of incidents, however, including drug offenses, the arrest usually takes place at a location other than where the offense occurred. One final source of missing addresses is that fact that PSMS does not allow an invalid address to be entered. Each address is verified against a list of known city addresses in its database. The list of addresses in PSMS is incomplete, however, never having been updated since its implementation. The only way data entry operators can override the system if PSMS rejects and address is to leave the address field blank. It is unknown what percentage of missing address can be contributed to this factor.
The above implied that, while the missing addresses still posed some problems, most missing addresses could be derived from the offense report location. As a result, whenever DMAP updates the PSMS data in its database, it first parses all of the reports associated with a case to determine whether there are any missing addresses. If there are no missing addresses the new data is committed to the database. On the other hand, if one or more addresses are missing, DMAP first checks to see whether the offense report associated with the case has an address. If this is true, then it is assumed that any other reports with missing addresses share the same address as the offense report. Only if none of the reports have an address is the data rejected.
Property ownership information is updated less frequently than 911 and PSMS data. Typically updates occur every six months. The source of the data is the City of Pittsburgh's real property file, which contains information regarding ownership, lienholders, tax status, zoning, assessed value as well as the date or purchase and amount of purchase. Since the real property file is simply a flat file there was no need to custom develop a database engine to handle the data. Updates are simply imported into an INFO file and geocoded.
Geocoding refers to the process of associating a data point with a geographic location based on some form of address. This address need not necessarily be a street or mailing address, but can be any key identifier of a particular location, such as the name of a place or the lot and block number of a property parcel. The geocoding methodology in DMAP was perhaps the most challenging aspect of its development. The problem is that while both the 911 system and PSMS verify each address after it is entered, they do not associate an xy coordinate with an address. In other words, they do not geocode addresses. In addition, they verify addresses against different, incompatible sources. The result is that an address which is verified as correct in the 911 system can be rejected by PSMS. In addition the addresses of offenders and victims in PSMS are not verified at all (mainly because a person may live outside of the city), and thus may contain many spelling errors. Thus some methods had to be developed to ensure that as many addresses from 911 and PSMS are correctly geocoded as possible.
Before an address is to be matched against a street coverage a first step is to parse the components of the address (such as street name, type, etc.) in order to ensure compatibility with the address format in the address coverage. This maximizes the number of data points that can be successfully matched. This step includes standardizing abbreviations for street types and street directions.
Once all addresses have been parsed the raw data file is ready for geocoding. During geocoding the computer attempts to find a matching address in the address coverage for each raw data point. If a match is found the xy coordinates of the matched address are added to the original data record. If the address coverage is a point coverage, the geocoded data will receive the same xy coordinates as the matched point in the address coverage. Data geocoded on polygon based address coverages obtain the xy coordinates of the geographic center of the matched polygon.
By far the most commonly used address coverage, however, is a line-based address coverage. For example, address coverages created with Tiger line files (available from the Census Bureau) are line based. An earlier version of DMAP used this type of address coverage. Geocoding with line-based coverages differs in that geocoded locations are only approximate. Instead of having an address for each polygon or point, line-based address coverages have an address range for each arc (line) representing a street. In most GIS systems each arc has a left and right beginning address and a left and right ending address. It is assumed that numbers on each side of the street have the same parity, i.e., even or odd. The entire arc shares the same street name, direction, suffix and type. During geocoding using line-based address coverages in ARC/INFO, the system first finds all arcs with the same street name, direction, etc. as the address that is to be matched. Once all candidate arcs are found, it tries to find an arc whose address range encompasses that of the data point to be matched. The exact xy coordinates of the geocoded location are then determined via interpolation on that arc. For example, if the starting and ending address of the arc are 100 and 200, respectively, and the address number of the data point to be matched is 150, then the geocoded location will be exactly half way along the arc.
Regardless of the type of address coverage, problems arise during geocoding when no exact matches can be found. There are two main causes for this: either ARC/INFO cannot find a matching street name or it cannot find a matching street number (this is particularly true for point or polygon based address coverages). Arc/Info provides a number of ways in which matching can be improved. The most commonly used one is to let the user choose one of a list of possible candidates obtained using a soundex algorithm. This is fine when only one or a few addresses are to be matched, but can become very tedious and time consuming when thousands of addresses are to be matched, as is the case in DMAP.
In developing DMAP it was soon found that geocoding requirements were unique and, unfortunately, well beyond the capabilities of ARC/INFO. The Tiger line files used in the earlier version of DMAP let to only 70% matches. This was mainly due to incorrect address ranges on the arcs and misspelled, incorrect or missing street names. This was clearly unacceptable for a system whose goal it was to support research, investigative and administrative functions because too much data was lost.
As a result it was decided to create a new point based address coverage based on both PAGIS property parcel data as well as City of Pittsburgh property tax files. The goal was not only to improve geocoding overall in terms of the proportion of data successfully matched, but also to pinpoint exact locations of incidents and calls for service rather than simply approximate their locations by means of interpolation. In addition, some way had to be found to match addresses for which no exact match could be found without having to go through a list of candidates for each unmatched data point. In creating the new address coverage for DMAP several problems were encountered that merit further discussion, since they impact the geographic accuracy of not only single data points, but by extension also data aggregated by areal units.
The common denominator between the City of Pittsburgh property tax file and the parcel coverage was the legal identifier for deeded land parcels, the lot and block number. Only the property tax file contained street addresses. The first step was to relate the two files via the lot and block number and use the property tax file's street address as the basis for the address coverage. However, having created the initial coverage it was found that on average only 40% of the addresses would address match. Upon closer inspection it was found that while the matchup rate between the parcel file and the tax file was 97%, a number of things were causing the poor results.
First, some of the street numbers associated with the property tax file were actually ranges (as in the case of apartment buildings, for example), while most of the parcels had only a single address associated with them. This posed a problem for ARC/INFO because it can only match based on address ranges or a single house number, but not a combination of both. Therefore, all data points associated with parcels having more than one address did not match.
Second, a large portion of PSMS and 911 call for service data (about 20%) is geocoded by intersection. In both systems an intersection will only geocode to the nearest 100 block address. In most cases, however, this is not a legitimate address. For example, the intersection of A and B streets might be recorded as 1000 B street with the 911 call for service address file. If such an address exists at the intersection of A and B streets, then all data at that location would also match in DMAP. However, if the closest address to the intersection were 1002 B street, then of course DMAP would lose fail to match incidents occurring at the intersection. This problem was a major contributor to the poor geocoding rate.
The third problem was that the city property tax file contained numerous spelling errors and inconsistencies. Street names were spelled incorrectly, street directions were missing, or street types were missing. In theory this could easily be fixed by manually going through each property file record and correcting any spelling mistakes. However, with 160,000 records this task proved to be insurmountable.
Finally, many streets in Pittsburgh are numbered streets. While Arc/Info can handle numbered streets, it does not recognize "2nd Ave." and "Second Ave." as being the same street. In addition, the tax file inconsistently uses numeric and alphanumeric representations of numbered street names.
In summary, a way had to be found to automatically account for and consider all of the above mentioned problems in such a way that an acceptable proportion of the data would geocode without extensive operator intervention.
The first step in the solution was to create a polygon based address coverage. This was done using the PAGIS parcel coverage with the lot and block number constituting the "address". Before the property file could be geocoded against this coverage, however, the problem of address ranges had to be resolved. This was done by writing a program in C to parse the tax file and create a duplicate entry for each valid street number in the address range of a particular property if the property had more than one street address. In doing so the parity of street addresses also had to be considered. For example, if the address range of a property was 100-106 Smith St., then the resulting property file after parsing would contain a record for 100, 102, 104 and 106 Smith St. where other than the street number all information was identical. The resulting parsed tax file thus contained one record for each unique address in Pittsburgh.
In creating the duplicate property file it was found that none of the public housing project parcels contained valid address ranges. In Pittsburgh many housing projects consist of several streets and buildings, where each building has its own address range. At the same time most housing projects comprise one large property parcel, and are associated with a single lot and block number. This makes it impossible to represent all street addresses in a single address field since more than a simple street range number is involved. Even if it were possible, however, all incidents in a housing project would geocode to the geographic center of the associated property parcel. Considering that most projects encompass quite a large area, it would be rather difficult to interpret a large number of incidents in the middle of a housing project.
The solution to this problem was to create pseudo parcels based on the building footprints of all structures contained in public housing projects. A separate polygon coverage was created using these building footprints, where each building polygon was assigned a lot and block number. This separate coverage was then appended to the original parcel coverage. Next, police officers equipped with maps of housing projects went on site to determine the address range for each building (surprisingly, the Pittsburgh Housing Authority could not provide such maps). After all building pseudo parcels had been assigned address ranges the parsing program described above was run again. To date not all of the housing projects have been completed due to the manpower limitation.
The parsed property file was then geocoded using the parcel based address coverage. About 97% of all property file records were successfully geocoded. The result of the geocoding was a point coverage containing one point for each successfully matched property record. In the case of address ranges one point for each address in the range was created. This resulting coverage was in turn converted to an address coverage based on the street address.
Initial testing showed that about 70% of PSMS data and 75% of call for service data was successfully geocoded. This was roughly equal to the Tiger line based address coverage. Clearly, this was still unacceptable. However, all addresses were matched "as is", i.e., no preprocessing was done in order to circumvent the problems outlined above and only the standard ARC/INFO geocoding capabilities were used. To further improve the geocoding rate a preprocessing program was designed and implemented using the C programming language and a hash table containing all valid street names in the city along with valid address ranges. The idea behind the hash table was to create the ability to find a closest matching address if no exact match was found, in particular as a solution to the intersection problem discussed earlier and, in the case of misspelled street names or omitted directions or types, automatically find and utilize the closest candidate. Finally, the preprocessing program automatically converts all numbered streets to their alphanumeric representation, i.e., "2nd Ave." to "Second Ave.", for example.
The hash table was created by first processing the parsed property file and extracting a list of all unique street names in the City of Pittsburgh. Next, the property file was processed again to find all valid street numbers for each street in the list. For each street an associated file was created containing a sorted list of street numbers. There are three hash keys in the table: the primary key is the street name, followed by the street type and direction. Each hash table entry points to a file containing the sorted street numbers.
The preprocessing program works as follows: first a backup copy is made of the original file containing the raw data to be geocoded. The backup file is then processed record by record, where each record's address is parsed and verified using the hash table. If the street name contained in an address is numeric, it is converted to its alphanumeric representation. Next, the program attempts to find an exact match for the street name, direction and type. If an exact match is found, the program looks up the associated list of street numbers and tries to find a matching street number. If a match is found the record is written back to the original file unaltered. If no match is found, the program finds the closest matching number, considering the parity. The address in the current record is altered and written back to the original table.
In the event that DMAP cannot find an exact match for the street name, a list of candidates is compiled using a soundex algorithm, taking into consideration the street type and direction. From this list the closest match (defined as the percentage of characters that match) is used and again DMAP proceeds to find the closest matching street number.
Using the preprocessing program DMAP was able to greatly improve the proportion of raw data that was successfully geocoded. For PSMS data the match rate is 95%, and for call for service data it is 97%. While not perfect, these levels are more acceptable than those of earlier geocoding attempts.
Random checks of those addresses which were altered were done in order to test the relative accuracy of the preprocessing program. It was found that in 75% of sampled cases the geocoded location was on the average only four to six street numbers away from the original. Only 5% of all altered raw data addresses geocoded more than a block away from the original address. This implies that, when data are aggregated by areal unit, the error rate in aggregation due to data points not being in their true areal unit is minimized.
2. 6 Data Collection and Aggregation
With the exception of census data, all of the data used in this dissertation were derived from geocoded data contained in DMAP. Since all of the empirical data was aggregated by either census tract or grid tile, a program was written to automate the aggregation. First, columns were added to the address coverage, one for each polygon layer in the DMAP geobase (for example, census tract and neighborhood boundaries). Next, each polygon in each layer was overlaid on the address coverage to determine which address points it encompassed. The corresponding boundary columns in the address coverage were then updated. The end result was that each record in the address coverage also contained the census tract number, neighborhood name, grid tile number, patrol sector, police zone number, fire district number and emergency response area number.
For PSMS and 911 incidents aggregating data by areal unit was then simply a matter of relating the geocoded data files to the address coverage via the address and running a frequency algorithm by areal unit and incident type (such as drug nature code or offense code) to produce counts by census tract, for example.
This section described the various data sources used in DMAP and in this dissertation, and outlined how the data were collected and processed. It is important to note that even though every effort was made to minimize the amount of data lost during geocoding and to maximize the quality of the data, any interpretation must take into consideration the factors outlined above.
However, despite all of the problems associated with the data set, DMAP to this day remains one of the few truly integrated geographic information systems. With the implementation of a new 911 and police records management system it is anticipated that the quality of data will increase further.
3. Modeling Street-Level Illicit Drug Markets
Urban geographers have long studied the ecology of crime; that is, the relationship between crime, the built environment, and land uses. A major impediment, however, has been the lack of data (Dunn, 1980; Sherman et al, 1989). Official police records systems generally have not controlled quality of address data; furthermore, it has been well documented that police under-report crimes; e.g., crimes that have low solvability factors. Several police departments, however, are in the process of implementing geographic information systems, thereby providing high quality location data and new opportunities to study the ecology of crime. Also, computer aided dispatch data from 911 emergency calls provide a new source of data for research, not subject to police screening.
This chapter uses data from the Pittsburgh Drug Market Analysis Program (DMAP) geographic information system to investigate the effect of traditional criminological, ecological, and enforcement factors on the formation of open-air, street-level drug markets. Pittsburgh, Hartford, Jersey City, Kansas City, MO, and San Diego were funded by the National Institute of Justice to develop DMAP systems. The purpose of DMAP are to: 1) support street-level drug case investigations, 2) identify drug markets, 3) track enforcement induced displacement of drug market "hot spots", and 4) evaluate street-level enforcement strategies.
Pittsburgh has had computer aided dispatching of 911 emergency calls for service since 1989 and computerized criminal offense and arrest reports since 1990. DMAP was implemented in 1991. All address data are verified on data entry into the CAD and police reporting systems, and DMAP has a land parcel-based point coverage for address matching that successfully places approximately 95 percent of police events on maps. Since drug offenses are generally victimless crimes, offense and arrest report data reflect police policy and management decisions in regard to allocation of scarce police resources, and not the actual activity levels of drug markets. Hence this study uses 911 call data, with the "drug" nature code, as the dependent variable. These are emergency calls to police, reporting drug-related offenses (e.g., illicit drug use or dealing). The 911 data do not have the under-reporting problems of offense and arrest reports, but have the limitation of being unconfirmed citizen perceptions of drug offenses. Officers responding to 911 calls attempt to verify the nature of calls and have the responsibility to revise recorded nature codes (robbery, vandalism, shots fired, etc.) as needed when radioing back to the dispatching center that they are cleared and available for responding to another call.
Section 2 provides a brief overview of drug enforcement approaches and section 3 reviews the ecology of crime literature. Section 4 provides a drug market model specification and describes the DMAP data used in this study. Section 5 provides modeling results of spatial econometric methods. Finally, section 6 concludes the chapter with a summary and future work.
There are opportunities for drug enforcement at each of the stages of illicit drug production and distribution. The illegal goods and market system consists of mostly foreign and some domestic crops, offshore and onshore processing/chemical manufacturing, transportation, distribution chains, and coordination between buyers and street-level dealers. Law enforcement agencies have tried, in varying degrees, to disrupt the production/distribution cycle at every stage. Enforcement higher up the production-distribution chain promises to cut supplies and increase prices, thereby reducing use.
In the late 1980s, there was a growing interest in street-level dealing as a weak link in the chain. The point of transaction between the street dealer and user is vulnerable: it is out in the open, money and drugs have to change hands, and it is difficult to relocate drug dealing points if disrupted and re-establish contacts. Drug dealers are unable to advertise, and are often hemmed in by turf claimed by other dealers.
Municipal police have several strategies for disrupting street-level drug markets in an effort to 1) increasing the time between successful transactions, thereby decreasing drug use; 2) increasing the safety of neighborhood residents by getting open-air dealers off the streets; and 3) using street-level contacts and arrests to identify mid-level and higher dealers for arrest. The Pittsburgh narcotics impact squad has several units and teams that sweep hot spot corners and bars, disrupting markets and arresting street dealers and users. Crackdowns saturate neighborhoods with narcotics police walking, patrolling, and disbanding groups of people in known drug markets. Community oriented policing puts foot patrol in communities to work directly with residents to identify long term solutions to drugs and other problems. Some situations, for example indoors dealing or working from the street-level up to mid-level dealers, require undercover or confidential informant buys. Purchased drugs are sent to the crime lab, and if positive result in warrants for arrest.
In response to enforcement, street-level dealing displaces in location, generally only a few blocks away. Before the Pittsburgh narcotics squad had weekend or 24 hour coverage, drug dealing often displaced to uncovered times. Corners that were impacted by street sweeps soon employed seller teams: lookouts, touters to attract and screen buyers, money holders and drug holders. Dealers commandeered or "rented" font porches to get the benefits of both public visibility and private property. Bars are attractive public facilities for drug dealing. Dealers and users can legitimately loiter, they can get lost in the crowd and toss drugs in a corner if the bar is raided, and there is limited guardianship controlling activities in and around bars.
DMAP has been successful in tracking displacement in time and space, identifying new hot spots before street officers do. After three years of police continually disrupting displaced hot spots, the two largest drug markets in Pittsburgh were dramatically improved.
3.3 Literature on the Ecology of Crime
The early ecology of crimes studies, starting with Clifford Shaw's seminal study of delinquency in Chicago (1929), tended to be descriptive, noting the concentration of crime in central business districts (CBD's). Concentrations of delinquents' varied inversely in proportion to distance from the city center. Delinquents were also located adjacent to heavy industry and commerce. Attending socioeconomic conditions were areas that tended to have physical deterioration, decreasing population, poverty, minorities, and immigrant population.
Schmid (1960) found similar patterns in Seattle, but also found crime pocketed in certain areas, like "skid row." Robbers commit robberies in CBD's, far from their residences. Robber offender characteristics included male unemployment, lower number of school grades completed, lower median income, and fewer people 14-and-over unmarried. Low family and economic status were highly correlated with robbery, larceny and auto theft. Family instability was an important factor contributing to delinquency. Research on criminal careers (e.g., Blumstein, Cohen and Farrington, 1988; Blumstein and Cohen, 1987) finds an at-risk age group - late teens to early twenties - that is more likely to commit crimes.
Lander (1954) found evidence that the percentage of non owner-occupied housing and percentage of nonwhite population was associated with delinquency. Since ethnic minorities, especially nonwhites also tend to have low socioeconomic and family status, poverty is generally the underlying causal factor for crime. Lander also found that "generally, higher rates of reported personal attack crimes prevail in lower-class residential areas of cities. Often these are predominantly black [areas]...Higher rates of property crimes are generally reported to characterize the central business areas of cities."
More recently there have been some studies providing insight or theories to the ecology of crime. Routine activities theory, due to Cohen and Felson (1979), states that criminal events result from motivated offenders, suitable targets, and absence of capable guardians against crime, and a converging of offenders and victims nonrandomly in time and space. This theory integrates several perspectives on crime, including frequency of convergence in time and space; rhythm, regular periodicity at which events occur; tempo, the number of events per unit of time; and timing/coordination of criminals and victims. Related literatures studied factors affecting motivated offenders, opportunity of availability of targets, lifestyles of victims, and the deterrent effects of official and unofficial policing implied by guardianship.
Sherman et al (1989) was the first to test routine activities theory with spatial data. Using 911 call data, this paper found substantial concentrations of police calls in relatively few "hot spots." Geographers have long recognized day-to-day clustering of people residing over wide areas into small nodes of activity (Brantingham and Brantingham, 1984). This is consistent with drug dealing observed in Pittsburgh. There are considerably more potential drug dealing points than actual hot spots, suggesting that a monitoring system is important to track enforcement-induced displacement, to keep drug markets disorganized.
Gorr and Olligschlaeger (1994) conducted an exploratory study, using weighted spatial adaptive filtering, with the 1991 data also included in this chapter. They found that the eleven open-air drug markets of Pittsburgh are, for the most part, located in areas with high percentages of black population (over 85% black). These drug markets, however, cover only somewhat more than half the total area with high black population, so that there are factors other than poverty/race at work. The four public housing drug markets were adequately estimated using percentage black population as the only explanatory variable and constant parameters over space relative to neighboring areas. The four public housing drug markets in Pittsburgh were adequately estimated using percentage black population as the only explanatory variable and constant parameters over space relative to neighboring areas. Public housing projects are homogenous in population and land use. The remaining seven markets, which have a mix of commercial and residential land uses, required spatially-varying parameters for the percentage black variable, to improve the fit of the data. In summary, the exploratory study suggested that characteristics other than those of the population of drug markets are necessary for modeling drug markets.
While previous authors applied routine activity theory to crimes with victims, this theory also has implications for illicit drug markets, on tacit coordination of dealers and buyers of drugs. Open-air drug dealing takes place in high poverty areas. Lower income persons generally have lower quality private space; e.g., higher levels of crowding in poor households. Hence, public spaces with low guardianship are primary candidates for open-air drug markets; areas such as run-down commercial strips, bars, and public housing projects with high proportions of female headed households. Skogan (1986) reported that fear of crime is higher among residents of high rise buildings than those living in smaller buildings. They feel that they do not have control of their environments and their space.
|
Table 3.1 Drug Market Model Variable Definitions and Expected Directions of Effects on the Dependent Variable |
|
|
Dependent Variable: |
|
|
DRGTOT |
Total 911 Drug Calls1 |
|
Traditional Demographic/Economic Crime Indicators : |
|
|
(+) POPN |
Population2 |
|
(+) PBLK |
Percentage Black Population2 |
|
(+) PAR |
Percentage At-Risk Population (Ages 12 to 24)2 |
|
(+) PFHH |
Percentage of Female-Headed Households2 |
|
(-) MDHHINC |
Median Household Income2 |
|
Ecological Crime Indicators |
|
|
(+) NBARS |
Number (of Nuisance) Bars3 |
|
(+) PCOMM |
Percent (of All Land Parcels Zoned) Commercial4 |
|
(+) PPHFAM |
Percent (of All Housing Units That Are) Public Housing Family5 |
|
(-) PPHELD |
Percent (of All Housing Units That Are) Public Housing Ederly5 |
|
Spatially Lagged Enforcement (Drug Dealing Displacement) Indicators: |
|
|
(+) SCONDGRA |
Sum of Contiguous Census Tracts' Drug Arrests |
|
(+) SCONIMPA |
Sum of Contiguous Census Tracts' Nuisance Bar Impact Raids |
|
1 Pittsburgh Police Bureau Computer Records2 1990 Census3 Nuisance Bar Task Force Records4 Allegheny County Property Tax File5 Pittsburgh Public Housing Authority Records |
|
Roncek and Maier (1991) found the number of taverns and lounges in city blocks in Cleveland positively associated with index crimes. Taverns' influence on crime was compounded when taverns were located in areas with more anonymity and lower guardianship. Note that five out of Sherman et al's (1989) top ten hot spots had bars. Eight out of the top twenty-five had bars.
3.4 Model Specification and Data
We used spatial overlay of 1990 census tract boundaries on police event and land parcel data for geocoding by census tracts. We then aggregated those data to annual, tract-level counts and sums for 1990 through 1992. Our goal was to investigate the power of ecological factors over traditional criminological modeling factors on 911 drug calls, and to investigate the effect of drug displacement using spatially lagged enforcement variables.
Table 3.1 defines the variables used in this study and their expected direction of influence on 911 drug calls for service. The dependent variable is the total number of 911 drug nature code calls for 1991 by census tract. One advantage of this measure of drug dealing is that drug calls are largely independent of narcotics squad resource allocations and activities. Less than 20 percent of drug calls are police initiated; the remainder are citizen initiated. A disadvantage of 911 data is that citizen caller behavior and perception underlay the data. For example, a resident may call 911 complaining that a youth gang is dealing drugs on his/her street corner, but the youths may not be dealing drugs at all. Responding officers are required to confirm the validity of initial call nature codes, but by the time that they arrive on the scene, a reported group may have disbanded or otherwise changed. Nevertheless, new drug hot spots detected with pin map displays of 911 drug calls have repeatedly been verified in Pittsburgh through follow-up police observation and found in aggregate to be an accurate indicator of the relative levels of drug dealing activity over time and locations.
The first group of independent variables are population characteristics traditionally used in criminological studies. Population (POPN) is simply a scale factor, which of course should be positively related to total drug calls. There are two advantages to placing this variable on the right hand side of the model, rather than dividing it into drug calls. First, we have run Poisson regressions (not reported in this chapter), appropriate for the count data of the dependent variable, which require the current formulation. Second, industrial census tracts and tracts in the central business district which are low in residential population are outliers when using calls per capita but are not unusual in the current formulation. Small sized populations are a liability as a denominator on the left hand side, but an asset on the right hand side in regard to outliers.
Percentage black population (PBLK) is highly correlated with measures of poverty (see Table 3.3 below); e.g., -0.583 with the log of median household income and 0.747 with female headed households. As discussed earlier, however, Olligschlaeger and Gorr (1994) found that about half of the black census tracts are in drug markets, so that other factors are at work in determining drug markets. The criminal career literature suggests that there is a crime-prone age group, so the next variable, percentage at-risk population, ages 12 to 24 (PAR) is included. A strong indicator of low social control and family status is the percentage of female headed households (PFHH). Finally, median household income is a direct measure of wealth and poverty. The expected direction of influence of all of these variables on drug calls is obvious.
The next group of variables in Table 3.1 are ecological measures. Pennsylvania has a nuisance bar law and Pittsburgh has a nuisance bar task force that 1) identifies bars chronically contributing to crime in neighborhoods, 2) directs a variety of enforcement strategies to correct problems, and 3) builds cases and initiates actions to close nuisance bars. Pittsburgh has about 60 nuisance bars, and a few are closed each year (DMAP has been instrumental in compiling and portraying information to close nuisance bars). Nuisance bars are primary drug dealing hot spots, both inside the bars and outside in the immediate vicinity.
Commercial land uses provide opportunities for drug dealers to linger and meet buyers, without the sense of personal guardianship and control over private spaces often present in residential areas. The percentage of land parcels that have commercial land uses (PCOMM) is a rough indicator of potential drug dealing areas.
The percentage of all housing units that are public housing units intended for families with children (PPHFAM) are highly vulnerable to drug use and dealing. Often physically and socially isolated, public housing communities are plagued by concentrations of social, economic and other limitations. By contrast, the percentage of all housing units that are public housing designed for the elderly (PPHELD) be characterized by lower levels of drug dealing activity, simply because of their inhabitants - it is difficult for young dealers and users to go unnoticed in these communities.
|
Table 3.2 Descriptive Statistics (n = 171 Census Tracts) |
|||||
|
Variable |
Year |
Mean |
Standard Dev. |
Minimum |
Maximum |
|
DRGTOT |
1990 |
29.6 |
71.3 |
0.0 |
598.0 |
|
1991 |
37.4 |
75.8 |
0.0 |
450.0 |
|
|
1992 |
36.4 |
74.3 |
0.0 |
440.0 |
|
|
POPN |
1990 |
2163.0 |
1336.0 |
12.0 |
8523.0 |
|
PBLK |
1990 |
29.2 |
34.1 |
0.0 |
98.8 |
|
PAR |
1990 |
18.9 |
9.8 |
1.9 |
76.7 |
|
PFHH |
1990 |
18.4 |
12.5 |
0.0 |
71.8 |
|
MDHHINC |
1990 |
21,158.0 |
10,353.0 |
4,999.0 |
82,553.0 |
|
NBARS |
1990 |
0.323 |
0.711 |
0.0 |
4.0 |
|
1991 |
0.284 |
0.664 |
0.0 |
4.0 |
|
|
1992 |
0.275 |
0.658 |
0.0 |
3.5 |
|
|
PCOMM |
1990 |
606 |
12.9 |
0.0 |
99.0 |
|
PPHFAM |
1990 |
4.0 |
16.5 |
0.0 |
100.0 |
|
PPHELD |
1990 |
1.2 |
6.9 |
0.0 |
82.1 |
|
SCONDRGA |
1990 |
109.3 |
166.0 |
0.0 |
944.0 |
|
1991 |
110.4 |
146.7 |
0.0 |
726.0 |
|
|
1992 |
101.8 |
142.6 |
0.0 |
718.0 |
|
|
SCONIMPA |
1990 |
20.9 |
33.8 |
0.0 |
152.0 |
|
1991 |
17.1 |
31.5 |
0.0 |
166.0 |
|
|
1992 |
12.0 |
22.0 |
0.0 |
102.0 |
|
The last two variables are indicators of potential drug displacement, computed as spatial lags (sums) of drug activities in contiguous census tracts. We used a rooks case, first order contiguity matrix with connections broken across Pittsburgh's three major rivers. The variables are the annual monthly sum of drug arrests in contiguous tracts (SCONDRGA), and a similar measure for nuisance bars raids in contiguous tracts. If large enough displacement occurs, we expect increased enforcement to positively influence drug calls in a nearby tract. Alternatively, these variables may serve merely as indicators of widespread drug market areas. We believe that we will be able to distinguish these two explanations in future relying on time series data that tracks levels of activity before and after enforcement actions.
Note that we did not include drug arrests and nuisance bar raids as variables for the tract of observation itself. Drug calls come to the attention of police and so eventually result in arrests. Likewise, drug calls generate nuisance bar raids at a later time. Increased police activity in an area may also stimulate increased willingness to report drug incidents by citizens. So there is a complex relationship between enforcement and drug calls. Future analyses will include these variables, lagged over time, in cross-sectionally pooled, monthly time series data.
Table 3.2 provides descriptive statistics for the variables of Table 3.1. There are 171 census tracts in the Pittsburgh DMAP system, covering approximately 60 square miles. Table 3.3 provides the corresponding simple bivariate correlations, with variables in the form used in models (some variables have been logged, or logged twice). Some multicollinearity is evident. Four pairs of independent variables have correlations exceeding 0.6.
|
Table 3.3 Pearson Correlation Matrix1 (with 1991 Data for LLDRGTOT, NUMBARS, LLSCONGRGA, and LLSCONIMPA |
||||||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
|
1. LLDRGTOT |
1.00 |
0.12 |
0.66 |
0.11 |
0.54 |
-0.48 |
0.47 |
0.16 |
0.26 |
-0.01 |
0.56 |
0.57 |
|
2. POPN |
0.12 |
1.00 |
-0.16 |
0.17 |
-0.08 |
0.18 |
0.02 |
-0.09 |
-0.01 |
-0.04 |
-0.08 |
-0.05 |
|
3. PBLK |
0.66 |
-0.16 |
1.00 |
0.05 |
0.75 |
-0.58 |
0.37 |
0.02 |
0.44 |
0.20 |
0.51 |
0.50 |
|
4. PAR |
0.11 |
0.17 |
0.05 |
1.00 |
-0.04 |
-0.13 |
-0.09 |
0.24 |
0.08 |
-0.07 |
0.19 |
-0.01 |
|
5. PFHH |
0.54 |
-0.08 |
0.75 |
-0.04 |
1.00 |
-0.65 |
0.15 |
-0.22 |
0.73 |
0.16 |
0.21 |
0.25 |
|
6. LMDHHINC |
-0.48 |
0.18 |
-0.58 |
-0.13 |
-0.65 |
1.00 |
-0.21 |
-0.16 |
-0.57 |
-0.31 |
-0.32 |
-0.25 |
|
7. NBARS |
0.47 |
0.02 |
0.37 |
-0.09 |
0.15 |
-0.21 |
1.00 |
0.28 |
-0.08 |
0.00 |
0.25 |
0.25 |
|
8. PCOMM |
0.16 |
-0.09 |
0.02 |
0.24 |
-0.22 |
-0.16 |
0.28 |
1.00 |
-0.11 |
-0.05 |
0.22 |
0.11 |
|
9. PHHFAM |
0.26 |
-0.01 |
0.44 |
0.08 |
0.73 |
-0.57 |
-0.08 |
-0.11 |
1.00 |
0.23 |
0.06 |
0.06 |
|
10. PPHELD |
-0.01 |
-0.04 |
0.20 |
-0.07 |
0.16 |
-0.31 |
0.00 |
-0.05 |
0.23 |
1.00 |
0.08 |
0.13 |
|
11. LLSCONDRGA |
0.56 |
-0.08 |
0.51 |
0.19 |
0.21 |
-0.32 |
0.25 |
0.22 |
0.06 |
0.08 |
1.00 |
0.62 |
|
12. LLSCONIMPA |
0.57 |
-0.05 |
0.50 |
-0.01 |
0.25 |
-0.25 |
0.25 |
0.11 |
0.06 |
0.13 |
0.62 |
1.00 |
|
1 Note that "L" at the beginning of a variable stands for "LOG" and "LL" stands for "LOGLOG". |
||||||||||||
Figure 3.1 is a map showing the correlation between percent black population at the census tract level and the level of 911 drug calls for service. High concentrations of drug calls are predominantly in tracts with high percentages of black population, but not all areas with high levels of black population have drug dealing. Some other factors must also be determining drug dealing besides race. Furthermore, race drops out of models estimated in the next section when underlying factors are entered such as measures of poverty and especially spatially lagged measures of drug enforcement.
|
Table 3.4 Progression of Models for 1990 (n = 171) |
||||
|
Dependent Variable: LOGLOG(DRGTOT) |
||||
|
COEFFICIENT |
MODEL 1 |
MODEL 2 |
MODEL 3 |
MODEL 4 |
|
CONSTANT |
0.367*** |
2.715*** |
2.020** |
1.425 |
|
Traditional |
||||
|
POPN (+) |
9.04E-5*** |
9.54E-5*** |
8.56E-5*** |
8.24E-5*** |
|
PBLK (+) |
0.00913*** |
0.00736*** |
0.00450*** |
0.00227 |
|
PAR (+) |
0.00155 |
0.00250 |
0.00169 |
|
|
PFHH (+) |
-0.000507 |
0.0105* |
0.0124** |
|
|
LOG(MDHHINC) (-) |
-0.236*** |
-0.184* |
-0.150* |
|
|
Ecological |
||||
|
NBARS (+) |
0.149*** |
0.158*** |
||
|
PCOMM (+) |
0.00514* |
0.00453* |
||
|
PHFAM (+) |
-0.00368 |
-0.00255 |
||
|
PPHELD (-) |
-0.00461 |
-0.00460 |
||
|
Lagged Enforcement |
||||
|
LOGLOG(SCONDRGA) (+) |
0.203* |
|||
|
LOGLOG(SCONIMPA) (+) |
0.0759 |
|||
|
R2 Adjusted |
0.484 |
0.517 |
0.613 |
0.642 |
|
F-Test |
80.658*** |
37.458*** |
30.855*** |
28.740*** |
|
Normality |
||||
|
Shapiro-Wilks |
0.987 |
0.983 |
0.978 |
0.986 |
|
Kiefer-Salmon |
0.985 |
2.729 |
14.641*** |
14.673*** |
|
Heteroscedasticity |
||||
|
Breusch-Pagan |
0.920 |
4.852 |
- |
- |
|
Koenker-Bassett |
- |
- |
11.775 |
15.554 |
|
White |
7.490 |
24.315 |
- |
- |
|
Spatial Dependence |
||||
|
Moran's I |
3.751*** |
3.037** |
2.855** |
1.269 |
|
Lagrange Multiplier (Error) |
12.140*** |
7.090** |
5.921* |
0.641 |
|
Kelehian-Robinson |
15.715** |
12.463 |
11.990 |
10.970 |
|
Lagrange Multiplier (Lag) |
10.164** |
9.263** |
6.714** |
0.015 |
|
Significance Levels: * = 0.05; ** = 0.01; *** = 0.001 |
||||
We used SpaceStat, written by Luc Anselin, to run multiple regression models based on the variables in Tables 3.1 and 3.2. Heteroscedasticity and non-normal errors were thought to exist in the data, given the clustering or hot spot nature of drug dealing. Hence we used the 1990 data to try several log (base e) transformations, in attempts to get the residuals into an acceptable form. Using SAS and SpaceStat, we found that double logs of the dependent and spatially lagged variables, plus logs of family household income were sufficient to handle these issues.
Tables 3.4 through 3.6 provide results of a progression of models for each year. For example, Table 3.4 is for 1990. Model 1 simply uses population and percentage black population to estimate drug calls. Both variables are highly significant with the expected signs, result in an adjusted R-squared of 0.484, have reasonably normal errors and no heteroscedasticity, but strong indications of spatial dependence in the errors and dependent variable.
|
Table 3.5 Progression of Models for 1991 (n = 171) |
||||
|
Dependent Variable: LOGLOG(DRGTOT) |
||||
|
COEFFICIENT |
MODEL 1 |
MODEL 2 |
MODEL 3 |
MODEL 4 |
|
CONSTANT |
0.410*** |
2.055* |
2.206* |
1.040 |
|
Traditional |
||||
|
POPN (+) |
8.36E-5*** |
8.75E-5*** |
8.43E-5*** |
7.59E-5*** |
|
PBLK (+) |
0.00975*** |
0.00834*** |
0.00578*** |
0.00168 |
|
PAR (+) |
0.000511 |
0.00113 |
0.00098 |
|
|
PFHH (+) |
0.000318 |
0.0110* |
0.0147*** |
|
|
LOG(MDHHINC) (-) |
-0.165* |
-0.158* |
-0.117 |
|
|
Ecological |
||||
|
NBARS (+) |
0.134** |
0.140*** |
||
|
PCOMM (+) |
0.00491* |
0.00371 |
||
|
PHFAM (+) |
-0.00466 |
-0.00309 |
||
|
PPHELD (-) |
-0.00886* |
-0.00921** |
||
|
Lagged Enforcement |
||||
|
LOGLOG(SCONDRGA) (+) |
0.247** |
|||
|
LOGLOG(SCONIMPA) (+) |
0.200*** |
|||
|
R2 Adjusted |
0.482 |
0.491 |
0.579 |
0.673 |
|
F-Test |
79.839*** |
33.785*** |
26.976*** |
32.795*** |
|
Normality |
||||
|
Shapiro-Wilks |
0.984 |
0.987 |
0.981 |
0.992 |
|
Kiefer-Salmon |
2.094 |
3.594 |
8.509* |
14.139*** |
|
Heteroscedasticity |
||||
|
Breusch-Pagan |
1.690 |
7.210 |
17.740* |
- |
|
Koenker-Bassett |
- |
- |
- |
11.008 |
|
White |
10.025 |
30.075 |
47.584 |
- |
|
Spatial Dependence |
||||
|
Moran's I |
5.329*** |
4.762*** |
3.345*** |
1.705 |
|
Lagrange Multiplier (Error) |
25.297*** |
18.798*** |
8.499*** |
1.504 |
|
Kelehian-Robinson |
28.545*** |
23.559*** |
14.652 |
12.882 |
|
Lagrange Multiplier (Lag) |
27.295*** |
27.102*** |
18.856*** |
1.120 |
|
Significance Levels: * = 0.05; ** = 0.01; *** = 0.001 |
||||
Spatial dependence tests have as the null hypothesis that no spatial dependence exists; hence, the highly significant test statistics for model 1 indicate spatial dependence. Moran's I, the Lagrange multiplier (error), and Kelehian-Robinson test all indicate that the model error terms have spatial dependence. In this case the OLS estimates are unbiased, but no longer efficient. The Lagrange multiplier (lag) indicates the more serious problem of a spatially lagged dependent variable. In this case, the OLS estimates are biased and all inferences are potentially incorrect, similar to a model with a significant omitted variable. Model 1 has both kinds of spatial dependence indicated.
Model 2 adds the remaining traditional demographic and socioeconomic measures. Note that the magnitude of the estimated coefficient for percentage black declines, as other variables highly correlated with race are included. Only the logged income variable is significant, and in the expected direction, and the adjusted R-squared increases only slightly to 0.517. Other diagnostics are similar as for model 1. While the spatial dependence statistics decline somewhat, they still remain strongly significant.
|
Table 3.6 Progression of Models for 1992 (n = 171) |
||||
|
Dependent Variable: LOGLOG(DRGTOT) |
||||
|
COEFFICIENT |
MODEL 1 |
MODEL 2 |
MODEL 3 |
MODEL 4 |
|
CONSTANT |
0.459*** |
2.376** |
1.802* |
1.042 |
|
Traditional |
||||
|
POPN (+) |
9.05E-5*** |
9.58E-5*** |
9.24E-5*** |
9.06E-5*** |
|
PBLK (+) |
0.00865*** |
0.00710*** |
0.00409*** |
0.00126 |
|
PAR (+) |
0.000126 |
0.00015 |
-0.00060 |
|
|
PFHH (+) |
0.000115 |
0.0136** |
0.0153*** |
|
|
LOG(MDHHINC) (-) |
-0.191* |
-0.155* |
-0.102 |
|
|
Ecological |
||||
|
NBARS (+) |
0.151*** |
0.139*** |
||
|
PCOMM (+) |
0.00679** |
0.00569** |
||
|
PHFAM (+) |
-0.00602** |
-0.00449* |
||
|
PPHELD (-) |
-0.00498 |
-0.00535 |
||
|
Lagged Enforcement |
||||
|
LOGLOG(SCONDRGA) (+) |
0.162* |
|||
|
LOGLOG(SCONIMPA) (+) |
0.206*** |
|||
|
R2 Adjusted |
0.441 |
0.459 |
0.579 |
0.648 |
|
F-Test |
68.132*** |
28.850*** |
26.971*** |
29.387*** |
|
Normality |
||||
|
Shapiro-Wilks |
0.980 |
0.982 |
0.991 |
0.995 |
|
Kiefer-Salmon |
1.755 |
0.721 |
0.032 |
1.574 |
|
Heteroscedasticity |
||||
|
Breusch-Pagan |
1.015 |
6.985 |
10.624 |
15.114 |
|
Koenker-Bassett |
- |
- |
- |
- |
|
White |
16.362** |
32.939* |
- |
- |
|
Spatial Dependence |
||||
|
Moran's I |
4.918*** |
4.442*** |
2.906** |
1.845 |
|
Lagrange Multiplier (Error) |
21.412*** |
16.051*** |
6.193** |
1.874 |
|
Kelehian-Robinson |
25.984*** |
25.346*** |
15.957 |
8.124 |
|
Lagrange Multiplier (Lag) |
22.654*** |
22.669*** |
13.594*** |
1.468 |
|
Significance Levels: * = 0.05; ** = 0.01; *** = 0.001 |
||||
Model 3 adds ecological variables, thereby providing a substantial increase in the adjusted R-squared to 0.613. Percentage black continues its decline in influence. Note that this is a common occurrence in criminological research: as factors closer to causal forces (e.g., poverty) are introduced, minority race tends to drop out. In this model the number of nuisance bars and percent of commercial properties are both significant, with the expected sign. There is some further decline in spatial dependence, which remains significant, nevertheless. Note, with this model the Kiefer-Salmon test for normality, which uses third and fourth moments of the estimated distributions, is strongly indicative of non-normal errors. The Shapiro-Wilks test, based on second moments, however concludes the opposite (with p-values of 0.97). Probability and other plots of the residuals show very acceptable, approximate normal distributions for the residuals.
|
Table 3.7 Comparison of Full Models Across Years (n = 171) |
||||
|
Dependent Variable: LOGLOG(DRGTOT) |
||||
|
COEFFICIENT |
1990 |
1991 |
1992 |
|
|
CONSTANT |
1.425 |
1.040 |
1.042 |
|
|
Traditional |
||||
|
POPN (+) |
8.24E-5*** |
7.59E-5*** |
9.06E-5*** |
|
|
PBLK (+) |
0.00227 |
0.00168 |
0.00126 |
|
|
PAR (+) |
0.00169 |
0.00098 |
-0.00060 |
|
|
PFHH (+) |
0.0124** |
0.0147*** |
0.0153*** |
|
|
LOG(MDHHINC) (-) |
-0.150* |
-0.117 |
-0.102 |
|
|
Ecological |
||||
|
NBARS (+) |
0.158*** |
0.140*** |
0.139*** |
|
|
PCOMM (+) |
0.00453* |
0.00371 |
0.00569** |
|
|
PHFAM (+) |
-0.00255 |
-0.00309 |
-0.00449* |
|
|
PPHELD (-) |
-0.00460 |
-0.00921** |
-0.00535 |
|
|
Lagged Enforcement |
||||
|
LOGLOG(SCONDRGA) (+) |
0.203* |
0.247** |
0.162* |
|
|
LOGLOG(SCONIMPA) (+) |
0.0759 |
0.200*** |
0.206*** |
|
|
R2 Adjusted |
0.642 |
0.673 |
0.648 |
|
|
F-Test |
28.740*** |
32.795*** |
29.387*** |
|
|
Normality |
||||
|
Shapiro-Wilks |
0.986 |
0.992 |
0.995 |
|
|
Kiefer-Salmon |
14.673*** |
14.139*** |
1.574 |
|
|
Heteroscedasticity |
||||
|
Breusch-Pagan |
- |
- |
15.114 |
|
|
Koenker-Bassett |
15.554 |
11.008 |
- |
|
|
White |
- |
- |
- |
|
|
Spatial Dependence |
||||
|
Moran's I |
1.269 |
1.705 |
1.845 |
|
|
Lagrange Multiplier (Error) |
0.641 |
1.504 |
1.874 |
|
|
Kelehian-Robinson |
10.970 |
12.882 |
8.124 |
|
|
Lagrange Multiplier (Lag) |
0.015 |
1.120 |
1.468 |
|
|
Significance Levels: * = 0.05; ** = 0.01; *** = 0.001 |
||||
Finally, model 4 adds the spatially lagged variables. Now percentage black is insignificant, but percent of female headed households and income are significant at conventional levels. The number of bars and percent commercial properties remains as in the previous mode - significant with expected signs. The lagged drug arrests variable is significant at the 0.05 level, but all spatial dependence has been eliminated.
Appendix B shows two maps comparing the residuals of models 1 and 4 for 1990. The breakpoints for the model 1 map use the model 1 RSME and the breakpoints for model 4 likewise use the model 4 RMSE. The maps show that model 4 has fewer and smaller spatial clusters of tracts with the same sign of residuals, reflecting model 4's success in eliminating spatial dependence.
The results for 1991 and 1992 are quite similar to those for 1990, in Tables 3.4 to 3.6. Table 3.7 places all of the results for model 4 and 1990-92 into one table for convenience. One difference between years is that the spatially lagged nuisance bar raids variable is highly significant only in the latter two years, 1991 and 1992. Inspection of Table 3.2 indicates that this finding is not induced by lack of variation in this variable in 1990. The decline in raids over the years are minor and the most striking finding is the consistency of results across years, and the strength of the ecological variables, including lagged enforcement variables, in accounting for geographic variation in levels of drug calls.
Model 4 has a high degree of nonlinearity and interactions due to its dependent variable which is a double log. To estimate the impact of some of the estimated coefficients on the number of drug calls in a census tract, we calculated estimates at the raw data level using model 4, 1991 coefficients from Table 3.5. Using the profile of a typical, mixed land-use, drug hot spot (POPN = 2,000, PBLK = 98, PAR = 15, PFHH = 26, MDHHINC = 15,000, NBARS = 3, PCOMM = 12, PHFAM = 0, PPHELD = 0, SCONDRGA = 400, SCONIMPA = 17) we estimate DRGTOT = 324. Reducing the number of bars to two reduces DRGTOT to 152, increasing the number of bars to four increases DRGTOT to 774. Increasing or decreasing the number of neighboring bar raids by one, increases or decreases the DRGTOT by 6. Increasing or decreasing the number of neighboring drug arrests by 50 raises or lowers DRGTOT by 20.
One potential threat to the validity of the results in Tables 3.4 through 3.7 is overly influential data observations. Hot spots of crime activity may lead to quite unusual observations that lie far removed from the data cloud of most observations. It could be the case, then, that some significant non-zero parameter estimates are merely due to the influence of a small number of extreme points, and without these points the coefficients would be non-significant. To test the robustness of the results, we removed highly influential observations using Belsley, Kuh and Welsch (1980) statistics and criteria (studentized residuals, hat-matrix diagonals for leverage; DFBETAS for coefficient sensitivity, and DEFITS for changes in fit). We re-estimated model 4 for each year, 1990-1992, with all observations deleted that met two or more test criteria. The number of excluded observations was 13 for 1990, 17 for 1991, and 18 for 1992.
A comparison of the results with those in Table 3.8 reveals of good deal of robustness. Of the statistically significant coefficients, none changed sign and only one became insignificant: PPHELD in 1991.PPHELD was only significant in 1991, and it appears that it was due to a single overly influential observation. Examination of the corresponding partial regression residual plot reveals one highly extreme data point that was subsequently removed.
Four coefficients that were insignificant in Table 3.8 become significant after removing the influential data points: LOGLOG(SCONIMPA) in 1990; PBLK, LOG(MDHHINC), and PHFAM in 1991; and LOG(MDHHINC) in 1992. All of the coefficients that were significant become more so.
The only coefficients that became less significant but remained significant were those for NBARS in 1991 and 1992. The change in estimated magnitudes for NBARS before and after the removal of influential observations were 0.158 to 0.164 in 1990, 0.140 to 0.114 in 1991, and 0.139 to 0.077 in 1992. Examination of the partial regression plots for 1991 and 1992 showed that the most influential data points removed were at extreme high values, but on the general trend line. These, as many of the points removed, may provide valid information for estimation. Nevertheless, in summary we find that the results hold up well when removing influential data points.
This chapter uses annual census tract data aggregated from police records and land parcel records, along with census data to model street-level drug markets in Pittsburgh. The dependent variable is annual 911 calls for emergency service with the drug nature code, providing a measure of illicit drug dealing. Traditional criminological theories suggest characteristics of populations correlated with crime, such as poverty, lack of guardianship, low family status, and at-risk age groups for modeling criminal events in areas. Ecological factors related to drug dealing are bars and lounges, availability of public space with low guardianship, and family public housing. Finally, drug enforcement causes drug dealing displacement, so spatial lags of drug arrests and bar impact raids should also contribute to drug calls.
Each group of variables makes a contribution to explaining 911 drug calls, and a number of variables in each group is significant with expected directions of impacts. Ecological factors provide a substantial increase in explanatory value over population characteristics, and the lagged spatial variables eliminate spatial dependence in the estimates.
Future work will next concentrate on pooled cross-sectional time series data with monthly observations. We believe that the before and after effects of enforcement activities will help delineate causal factors, using Granger (1969) causality. We plan to incorporate insights obtained from the annual research into the new effort, including double log transformations to provide normal errors and spatial lags of enforcement variables to eliminate spatial dependence.
4: Weighted Spatial Adaptive Filtering: Monte Carlo Studies and Application to Illicit Drug Market Modeling.
Damped negative feedback is a mechanism that has found widespread use in estimating time-varying parameter models; for example, see Robbins and Monro (1951), Brown (1962), Carbone and Longini (1977) and Makridakis and Wheelwright (1977). The underlying assumption of these techniques is that all past data points influence the current one, but with strength that declines exponentially with the age of the data. Time-ordered recursive calculations using the feedback of a single one-step-ahead forecast error at each step yield parameter estimates with this property.
More recently Foster and Gorr (1986) have applied damped negative feedback to estimating spatially varying parameters in the development of the spatial adaptive filter (SAF). The underlying assumption of SAF, following from the gravity model of spatial influence, is that all observation points interact simultaneously, but with strength that declines exponentially with distance between two points. SAF thus uses multiple feedback signals at each observation points in an iterative procedure applied simultaneously to all observation points. These signals are one-step-ahead spatial forecast errors made from neighboring observation points of a point undergoing parameter adjustment. Note that SAF is distinct from the spatial filtering method due to Getis (1994). While the spatial adaptive filter deals with spatial heterogeneity in the form of spatially varying model parameters, the latter provides a data transformation to remove spatial dependence from the variables of multiple regression models, analogous to generalized differencing used to remove serial correlation from time series data.
This chapter addresses the question: "How can we best combine multiple feedback signals for parameter revision in damped negative feedback algorithms?" SAF uses only simple arithmetic averages of signals and therefore provides equal weight to both potentially "appropriate" and "inappropriate" feedback. This paper proposes a new pattern recognition approach to combining multiple feedback signals employing weighted averages similar to those used in combining time series forecasts (for example, Bates and Granger, 1969). The pattern recognizer automatically rewards successful signals with positive weights and penalizes poor ones with near zero weights.
The resulting weighted spatial adaptive filter (WSAF) enhances adaptive filtering's ability to automatically identify and estimate parameters with discontinuous or sharp gradient changes occurring over space. WSAF also reduces or eliminates the need for correction limits intended to curb the influence of outlier data points (for example, the correction limit on damped negative feedback as used by Carbone and Longini, 1977), making it a robust estimator of spatially varying parameters.
The second section of this chapter briefly reviews the varying parameter model specification, its applications, and estimation methods. The third section reviews the SAF algorithm. This is followed, in the fourth section, by the proposed extension for multiple feedback signals. The fifth and sixth sections include the design and results respectively of Monte Carlo experiments for testing and illustrating WSAF in comparison to SAF and OLS regression. The seventh section presents a brief case study contrasting SAF and WSAF for expansion modeling the illicit drug market areas in Pittsburgh, Pennsylvania. The last section provides a brief conclusion.
4.2 Varying Parameter Models and Methods.
Anselin (1988, p. 13) notes that "In the literature of regional science and economic geography, there is ample evidence for the lack of uniformity of the effects of space. Several factors, such as central place hierarchies, the existence of leading and lagging regions, vintage effects in urban growth, etc. would argue for modeling strategies that take into account the particular features of each location (or spatial unit)." A corresponding expression of spatial heterogeneity is in the varying-parameter model:
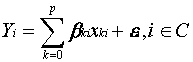 (4.1)
(4.1)
where C is an index set of the time and/or space context of parameter variation, i is an index in C, Yi is the dependent variable observation in context i, b ik is the parameter for the kth independent variable (k = 0,1,2,...p), and e i is the error term centered at zero. This model in unconstrained form is, of course, nonimplementable because the number of parameters increases with the number of observations (Anselin, 1988, p. 120). Hence there are several strategies, apparent later in this section, for limiting the number of degrees of freedom used to represent variation of the b ik over C.
Estimates for model (4.1) may be of direct use in many practical decision support applications. For example, cost/benefit considerations often make it infeasible to collect the data required for fully specified models. This accounts, in part, for the wide application of exponential time smoothing time series models for inventory control applications. Consumption of a good is a function of the manufacturer's price, the price of competitor's products, other attributes of the good and competitor's goods, advertising expenditures, the state of the economy, etc. However, smoothing models, using only time and seasonal indicators, self-adapt to structural changesikik in time series and provide up-to-date models for extrapolative forecasts of sufficient accuracy for production planning.
A major use for varying parameter model (4.1) is in exploratory data analysis (for example, Bretschneider and Gorr 1983, Foster and Gorr, 1986 and Cleveland and Devlin, 1988). While residual tests for cross-sectional models (for example, Moran's I) may detect unmodeled spatial heterogeneity in a conventional homogenous model, map displays of subsequently estimated spatially varying parameters for the same model may reveal which parameters vary significantly and the detailed shape or form of variation. In turn, this information may suggest additional theory or provide tentative evidence of promising additional model structure. Note that SAF uses nonvarying parameter estimates as initial values, and then optimizes spatial variation centered around the initial values. Hence this method, like residual tests, rightfully can be classified as providing diagnostics for conventionally estimated models.
Exploratory modeling is often a component in expansion modeling; for example, through the use of step-wise regression models employing polynomials or other functions of time and/or spatial coordinates interacted with an initial model's variables (Casetti, 1972, 1973, 1986; Casetti and Jones, 1992). Functional expansions provide one approach to estimating model (4.1) and have the advantage of providing significance testing for spatial variation. Such expansions, however, limit parameter variation to the form assumed, and rapidly introduce multicollinearity with increasing number of terms. For instance, Foster, Gorr and Wimberly (1992) found that polynomial expansions were unable to detect a significant time variation found using moving window regression. SAF, like window regression, provides nonfunctional expansions; no functional form is assumed.
A promising application of WSAF to expansion modeling is for the case of cross-sectional models with discrete parameter changes by region in which the number of regions and their boundaries are unknown. The initial model is a multivariate specification which does not include any reference to regional differences, and is estimated using a conventional method. The resulting parameter estimates serve as initial values for WSAF. Choropleth map displays of WSAF's varying-parameter estimates (such as in Figures 4.2, 4.6 and 4.7 below) allow the modeler to identify regions and their boundaries. Finally, the initial model and discrete regional expansions can be incorporated into a spatial switching regression (the terminal model) estimated using maximum likelihood estimation (see Anselin 1988, p. 132).
Two additional methods for estimating model (4.1) are locally weighted regression (for example, Cleveland, 1979; Casetti, 1982 and Cleveland and Devlin, 1988) and Kriging (for example, David, 1977, Haining, 1990). Both of these methods estimate a separate model for each observation point using a weighting function that generally decreases the influence of other observations with distance. Note that the multiple feedback signal weighting in WSAF is different from the weighting for declining influence between data observations with distance. The former is unique to WSAF. The latter is common to locally weighted regression, Kriging, and SAF/WSAF.
In locally weighted regression, the weights are exogenously specified, by trial and error, and can take any form. Cleveland (1979) and Cleveland and Devlin (1988) develop locally weighted regression without specific regard to geographic theory or application, and focus on the fit of the dependent variable rather than on spatially varying parameters. These authors provide some statistical properties for their overall estimates. Casetti (1982) develops locally estimated regressions in the context of geographical applications, and draws attention to the spatially varying parameter estimates.
Developed for geostatistical ore reserve estimation, Kriging uses an empirically estimated function, the variogram, to determine spatial weighting of data observations, most often in a univariate model specification. The variogram is the expected value of the squared deviation of yi at observation vector xi versus at xi + hi, for all vectors hi comprising the study region (or volume) relative to xi, and yields all variance and covariances needed for B.L.U.E. estimation in Kriging.
One constraint employed to reduce the considerable sample size requirements of Kriging is to use a spherical variogram, that is, assume that the variogram is homogenous with regard to direction. Anisotropies, however, are generally encountered - in ore deposits, especially in vertical versus horizontal directions, and in regional science applications due to reasons like those enumerated at the start of this section. Indeed, empirical estimation of weighting functions, allowing for anisotropies, is an advantage of Kriging over locally weighted regression.
The multivariate version of Kriging, cokriging, employs and extension of the variogram, the covariogram, which in its most general form has the number of variance and covariance terms required for estimation increasing with the square of the number of independent variables for each observation point, and direction and distance from the observation point. So while Kriging and cokriging are attractive in terms of their rigorous and rich formulation, they point out the enormous sample size requirements of such an approach.
Lastly, we enumerate properties of SAF, relative to other methods for estimating model (4.1):
(1) SAF incorporates spatial autocorrelation directly into spatially varying parameters by linking parameter estimates through contiguity relationships, exponentially declining weighting of influence with distance, and damped negative feedback. The degree of exponential influence decline is determined endogenously. Furthermore, SAF automatically handles additional heterogeneity in parameter variation through a tracking signal that increases feedback sensitivity locally.
(2) WSAF is the only method of those examined here, with exception possibility of Kriging, that can automatically estimate discontinuities in spatial parameters without a priori specification (for example, without regional indicator variables). The multiple feedback signal weighting that leads to sharp distinction of discontinuities can also automatically account for anisotropies by screening out inappropriate feedback for a given observation location.
(3) SAF, like locally weighted regression and Kriging, provides nonfunctional varying parameters; that is, no functional form for variation is assumed. A benefit of this is that SAF can readily accommodate multimodal parameter surfaces, whereas, polynomial or other parametric expansions have inherent limitations. For example, Casetti and Fan (1991) found that a polynomial expansion for county-level AIDS incidence in Ohio counties provides only a course-grained representation of the roughly ten peak areas in the state. A limitation of nonfunctional varying parameters is that SAF estimates cannot be extrapolated or interpolated without additional model fitting. Kabel (1992) employs time series model extrapolations of WSAF parameter estimates for given counties to forecast the spatial diffusion of AIDS incidence. WSAF was applied independently for approximately forty cross-sectional data sets, obtained by quarter over a ten-year period.
(4) SAF's parameter estimates are nonlinear combinations of dependent variables values; hence, SAF has no standard distributional properties. It is strictly an exploratory method. Functional expansions and locally weighted regressions provide some significance testing for varying-parameter models.
(5) SAF and WSAF, while optimizing a standard criterion function to optimize negative feedback selectively for each independent variable of model (4.1), will be classified as heuristic methods. Indeed, Monte Carlo studies, like those provided below, are necessary to determine the performance of adaptive filters in terms of their individual capabilities and in comparison with other methods. Our knowledge of their performance is limited at this time.
SAF's lineage of damped negative feedback estimation includes both exponential smoothing (Brown, 1962) and adaptive filtering (Widrow and Hoff, 1960; Makridakis and Wheelwright, 1977; and Carbone and Longini, 1977) time series methods. The smoothing methods are univariate, but include optimization of smoothing (or damping) factors to determine optimal tracking of change of individual model parameters (intercept, time trend, and seasonal factors) using a squared error criterion based on one-step-ahead forecast errors. The focus on short-run forecast performance tends to reduce overfitting while keeping a model up to date.
The adaptive filters extend damped negative feedback estimation to multivariate model (4.1), but do not selectively tune damping factors for optimal tracking. SAF combines smoothing and adaptive filtering by optimizing individual damping factors for each b k in model (4.1).
At iteration p the SAF algorithm produces a set of spatial forecasts for observation i using the previous iteration's coefficients of the observations in its neighborhood:
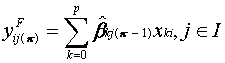 (4.2)
(4.2)
The neighborhood of an observation for contiguous influences may be defined as the set of all points I, where I = {j | Dij £ r, j ¹ i}, Dij is the distance from point i to point j, and r is the neighborhood's radius. An alternative definition for data aggregated to areal units is the set of all areal units, I, contiguous to current observation i's area unit. The forecasts are analogous to ex ante econometric model forecasts that use coefficients estimated from historical data but independent variables from the forecast period. Such forecasts isolate the cause of forecast errors to inappropriate parameter estimates and residual noise, assuming the independent variable values to be free of measurement error.
The set of forecasts produced by an observation's neighbors is then used to compute a corresponding set of updated parameters:
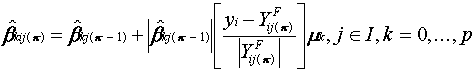 (4.3)
(4.3)
where the component in brackets is the overall feedback signal from j to i and m k Î (0,1) is the damping factor for the kth parameter. This feedback equation incorporates the Carbone/Longini (1977) percentage update scheme which scales overall feedback for each coefficient. It is similar to the Widrow-Hoff (1960) rule, or Perceptron convergence procedure used in Minsky and Papert's (1969) Perceptron, and the standard delta rule used to estimate feedforward artificial neural networks (Rumelhart and McClelland, 1988).
In order to reduce the influence of outliers a correction limit is added imposing an upper limit on the magnitude of adjustment:
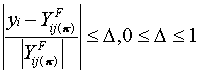 (4.4)
(4.4)
The estimate for the kth parameter of observation i at iteration p is the average of the set of updates obtained in (4.3):
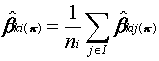 (4.5)
(4.5)
where ni is the number of neighboring observations in I.
Tobler's (1979) first law of geography that "everything is related to everything else, but near things are more related than distant things" is directly built into SAF estimation. Suppose, for exposition purposes, that we limit the following discussion to areal units. At the end of its first iteration, only the contiguous neighbors of an areal unit have contributed to its parameters' estimates. Since, however, the SAF algorithm is applied simultaneously to all observation points, at the start of the second step contiguous neighbors will have been affected by all of their respective contiguous neighbors. Hence some areal units "twice removed" from the units undergoing revision will participate in the revision. Those units "twice removed" have their feedback damped twice by multiplication of m ks. Each iteration expands the extent of data points in this manner. Influence thus decreases roughly exponentially with distance from point i (Foster and Gorr, 1986).
Initial estimates for the parameters, b ki(0), are usually obtained by estimating a constant parameter version of model (4.1), for example, using ordinary least squares regression. In general, the initial values will be biased (Anselin, 1988); however, SAF is expected to modify them to remove biases. It is desirable to obtain initial values that are spatial averages of unbiased varying parameters since SAF tends to center its estimates on the initial values.
SAF conducts an optimization (an exhaustive grid search at this stage of research) to determine the optimal set of damping factors (m *k, k = 0,...,p) as determined by the mean absolute percent error of one-step-ahead spatial forecasts:
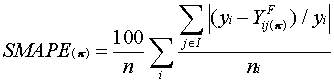 (4.6)
(4.6)
The set of optimal damping factors is the one that produces the lowest SMAPE after applying a stopping rule to determine the number of iterations necessary for convergence. Foster and Gorr (1986) proposed two alternative stopping rules. One is that iterations stop when SMAPE(p -1) - SMAPE(p ) £ d , where 0 < d < 100. The second is to stop after a fixed number of iterations, determined through experience with Monte Carlo experiments.
An alternative criterion to the SMAPE is the mean absolute percentage of estimation fit errors (FMAPE), computed as:
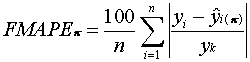 (4.7)
(4.7)
where
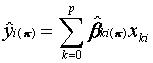 (4.8)
(4.8)
Generally the SMAPE converges more quickly than the FMAPE, and when used as the basis of a convergence criterion reduces the tendency of adaptive filters to overfit data.
The optimization of damping factors provides a form of pattern recognition. In cases where a single parameter varies systematically over space and other parameters are constant, the optimal damping factor for the varying parameter tends to be "large" in value and those for the constant parameters tend to be zero (Foster and Gorr, 1986). Thus the optimization correctly attributes overall spatial variation to the varying parameter in the limited cases examined to date.
SAF optionally includes a spatial adaptation of the Trigg/Leach (1967) tracking signal to automatically detect and model spatial autocorrelation (see Foster and Gorr, 1986). When encountering contiguous groups of mostly positive or mostly negative residuals, this signal locally increases damping to change parameters in the appropriate direction to better fit the data locally. In particular, we multiply each damping factor m k by the spatial tracking signal
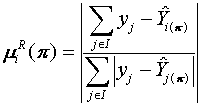 (4.9)
(4.9)
The signal is similar to Moran's I or Geary's C statistics applied to model residuals, except that the results are incorporated back directly into estimation rather than just being diagnostics.
4.4 Multiple Feedback Pattern Recognizer
Due to signal averaging in equation (4.5) all neighbors of a given spatial location carry equal importance in determining the magnitude and direction of adjustment at each iteration of SAF. In the first iteration the parameters of all observations are equally successful in predicting the current observation's independent variable since the initial parameter estimates are generally the same for all observations (being spatially constant estimates). Equal weights are therefore justified. However, in the presence of spatial variation in one or more of the parameters, observations will have varying success in the second iteration with such variation becoming more pronounced as the number of iterations increases. As a result, if there are large differences between the true parameters of neighboring observations, for example, due to step jump running through the neighborhood, then the algorithm will tend to smooth out these changes rather than recognize sudden drops or increases. This potentially introduces a bias into estimates.
It is therefore desirable to incorporate a pattern recognizer into SAF that reduces this bias. One way to accomplish this is to determine the success of each individual spatial forecast, (4.2), from j to i and weight the influence of each neighbor accordingly. One modification of (4.5) is thus:
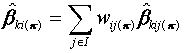 (4.10)
(4.10)
where
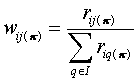 , (4.11)
, (4.11)
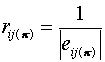 if | eij(p
) | > .01, 100 otherwise, (4.12)
if | eij(p
) | > .01, 100 otherwise, (4.12)
and
![]() (4.13)
(4.13)
The resulting adaptive filter obtained by substituting (4.9) for (4.5) is WSAF. Note that this scheme eliminates the need for correction limit (4.4) since the weights in (4.9) automatically screen outliers.
Equation (4.10) is similar, algebraically, to weighting schemes used in time series combination forecasting (for example, see the seminal work of Bates and Granger, 1978, and the comprehensive bibliography by Clemen, 1989). The weights of this chapter, however, are used for a somewhat different purpose. Based on the magnitude of forecast errors, they automatically sense appropriate versus inappropriate sources of feedback signals for updating parameters of varying-parameter model (4.1).
This section uses simulated data with known parameters, generated via Monte Carlo techniques, to compare WSAF to SAF. The spatial domain of parameter variation consists of coordinates (x1i,x2i), i = 1,...,100 taken from a uniform, two-dimensional ten-by-ten grid. In all cases the neighborhood I of an observation is defined as any non-diagonal contiguous observation on the grid (that is, the rook's case). Therefore a neighborhood consists of at most five points including the point with parameters to be updated. The general form of the stochastic process being simulated is represented by the following model:
![]() (4.14)
(4.14)
where
![]() (4.15)
(4.15)
Both independent variables are randomly drawn from a normal distribution and thus contain no information on any spatial variation of the parameters. Unless otherwise specified the parameters have no spatial variation and take on the following values: b 0i = 15.0, b 1i = 2.0, b 2i = 2.0.
We study three different cases of (4.14) with respect to parameter variation. In the first case, "constant parameters," the parameters are as specified as above and do not vary spatially. Ideally, SAF and WSAF should not estimate any spatial variation and therefore assign zero damping factors to all parameters. Initial OLS estimates should therefore stand as the final estimates.
In the second case, "linear decline of a non-intercept parameter," b 1i declines linearly with distance from point (z1i,z2i) = (7,3):
![]() (4.16)
(4.16)
The maximum value of b 1i, 2.0, occurs at (7,3), and the minimum, 1.28, at (1,10). In this case SAF and WSAF should assign positive damping factors to b 1i and zero damping factors to the other two parameters. Since the decline in b 1i is linear with distance, the influence of neighboring observations is roughly equal so that simple averages of spatial feedback signals should perform well. Thus SAF should have performance about equal to that of the WSAF in improving the parameter estimates for b 1i.
The final case, "step jump in intercept," introduces a step jump in the intercept from 5.0 to 15.0. The step jump can be thought of as the result of a barrier limiting the influence of regions on each other. To make it more difficult for SAF to recognize the spatial pattern of parameter variation, we divide the grid along an irregular border including a thin strip of "territory" from (10,1) to (10,5) and an "enclave" at point (9,5) (see Figure 4.2 below where the upper left region in each map has the intercept of 15). SAF and WSAF should assign a positive damping factor to the intercept and zero damping factors to the other parameters. WSAF should be superior in this case as there are many opportunities for weighted spatial feedback signals to screen out inappropriate signals.
Ten replications were generated for each case using a random number generator for the independent variables and error term values, resulting in a total of thirty data sets, and three thousand observations of estimated versus true parameters. All data sets were process by SAF and WSAF using OLS estimates as initial parameter values. For SAF we used the same procedures as in Foster and Gorr (1986), namely, a correction limit of 0.5 and eight iterations for convergence; however, the Trigg/Leach signal option was not used.
In the presence of spatial parameter variation both SMAPE and FMAPE decline monotonically as a function of the number of iterations until they reach their respective minimums (see the example of Figure 4.1). Then each tends to oscillate slightly around its minimum. SMAPE generally reaches its minimum first. Continuing to iterate beyond the point of SMAPE's minimum results in overfitting. Consequently, we used the rule of stopping iterations when SMAPE increases. Also, in order to account for random fluctuations in both measures in the absence of spatial parameter variation, we also stop iterating if FMAPE increases. The optimum parameter values are those that are computed in the iteration prior to the one in which on of the two stopping rules fire.
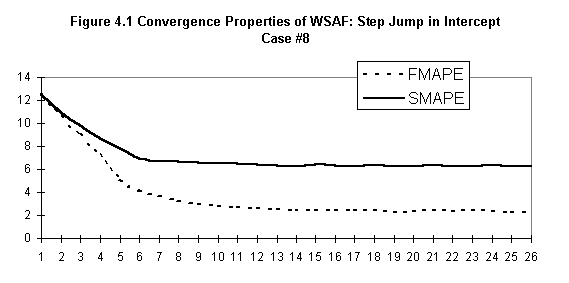
Since both SAF and WSAF use OLS regression as initial parameter values, it is relevant to compare the estimates produced by those adaptive filters to OLS estimates to see if they make any improvements in fit performance. Thus we calculate the percent improvement in the fit (mean absolute percent error) and bias (mean percent error) of SAF and WSAF over OLS with respect to the model and parameters.
|
Table 4.1 Improvement of SAF and WSAF over OLS (Median of 10 Replications) |
||||||
|
Constant Parameters |
Linear Decline of Nonintercept |
Step Jump in Intercept |
||||
|
SAF |
WSAF |
SAF |
WSAF |
SAF |
WSAF |
|
|
Model (Y): |
||||||
|
MAPE |
14.6 |
0.0 |
66.2 |
74.6 |
70.1 |
76.3 |
|
MPE |
10.8 |
0.0 |
63.6 |
48.1 |
70.1 |
72.8 |
|
b 0i: |
||||||
|
MAPE |
-3.3 |
0.0 |
0.0 |
0.0 |
41.6* |
60.7* |
|
MPE |
0.3 |
0.0 |
0.4 |
0.0 |
33.8* |
45.9* |
|
b 1i: |
||||||
|
MAPE |
0.0 |
0.0 |
54.8* |
51.8* |
0.0 |
0.0 |
|
MPE |
0.0 |
0.0 |
46.4* |
33.8* |
0.1 |
0.0 |
|
b 2i: |
||||||
|
MAPE |
0.0 |
0.0 |
0.0 |
0.0 |
-0.1 |
0.0 |
|
MPE |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
|
Optimal m k: |
||||||
|
b oi: |
0.3 |
0.0 |
0.1 |
0.0 |
0.9 |
0.7 |
|
b 1i: |
0.0 |
0.0 |
0.9 |
0.5 |
0.3 |
0.0 |
|
b 2i: |
0.0 |
0.0 |
0.1 |
0.0 |
0.2 |
0.0 |
|
*Statistically significant difference between SAF or WSAF and OLS at the 0.01 level using the Wilcoxon signed rank test |
||||||
Table 4.1 presents the fit results of the Monte Carlo simulation while Table 4.2 tabulates the distribution of the optimal damping factors for each case. With the exception of the constant parameter case, both versions of SAF significantly improve the overall fit of the model over OLS, as expected. Furthermore, WSAF outperformed SAF in a number of areas, also as expected.
First, in the constant parameter case SAF and WSAF should not have been able to improve over the OLS estimates due to the absence of spatial variation in the parameters, and all damping factors should be zero. Table 4.2 shows that this is not the case, however, for SAF. Only the second parameter consistently has zero damping factors. In fact, none of the ten replications resulted in zero damping factors for all three parameters. By contrast, WSAF had zero damping factors for all parameters in seven out of the ten replications. In the median case SAF was able to slightly improve the overall fit of the model (the median OLS R2 was 0.85 which SAF improved to 0.89); however, this was due to overfitting as evidenced by the worse fit for b 0 by SAF.
|
Table 4.2 Optimal Damping Factors from Ten Replications of Monte Carlo Cases |
||||||||||||
|
Damping |
Frequency of Optimal Damping Factors |
|||||||||||
|
Case |
Method |
Factor |
0.0 |
0.1 |
0.2 |
0.3 |
0.4 |
0.5 |
0.6 |
0.7 |
0.8 |
0.9 |
|
Constant |
SAF |
m 0 |
2 |
2 |
3 |
1 |
2 |
|||||
|
m 1 |
10 |
|||||||||||
|
m 2 |
6 |
2 |
1 |
1 |
||||||||
|
WSAF |
m 0 |
7 |
3 |
|||||||||
|
m 1 |
10 |
|||||||||||
|
m 2 |
9 |
1 |
||||||||||
|
Linear |
SAF |
m 0 |
3 |
2 |
4 |
1 |
||||||
|
m 1 |
1 |
3 |
6 |
|||||||||
|
m 2 |
5 |
3 |
1 |
1 |
||||||||
|
WSAF |
m 0 |
6 |
1 |
3 |
||||||||
|
m 1 |
2 |
3 |
2 |
2 |
1 |
|||||||
|
m 2 |
6 |
4 |
||||||||||
|
Step Jump |
SAF |
m 0 |
1 |
9 |
||||||||
|
m 1 |
2 |
1 |
2 |
2 |
2 |
1 |
||||||
|
m 2 |
4 |
1 |
1 |
1 |
2 |
1 |
||||||
|
WSAF |
m 0 |
1 |
1 |
4 |
2 |
2 |
||||||
|
m 1 |
5 |
5 |
||||||||||
|
m 2 |
6 |
3 |
1 |
|||||||||
The results of the linear decline case show that WSAF provides a slightly better fit than SAF (although the improvement of the MPE is lower). Also, the optimal damping factors are more consistent for WSAF. Table 4.2 shows that the distribution of damping factors for those parameters without spatial variation is clustered around 0.0 for WSAF, whereas it has more dispersion for SAF. WSAF also seems to be better able to identify those parameters that vary spatially. The median damping factors for b 0 and b 2 are zero for WSAF but erroneously positive for SAF. In addition, the damping factors for b 1 are generally lower for WSAF and more evenly distributed.
The step jump case provides conditions favoring WSAF. Although the improvement in the overall fit of the model is not substantially better (76.3 percent for WSAF versus 70.1 percent for SAF), WSAF improves the spatially varying parameter (b 0) estimates by 46 percent over SAF for the MAPE and 36 percent for the MPE in the median case. The difference is significant at the 0.01 level using the matched pairs Wilcoxon signed rank test. Also, the distribution of WSAF's optimal damping factors reflects the actual variation more accurately (see Table 4.2). The optimal damping factors for the nonvarying parameters are widely dispersed for SAF, whereas for WSAF they are near 0.0, as in the linear decline case.
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
||
|
1 |
13 |
13 |
11 |
12 |
13 |
13 |
13 |
13 |
12 |
11 |
1 |
15 |
15 |
13 |
13 |
15 |
15 |
15 |
15 |
14 |
13 |
|
2 |
12 |
13 |
13 |
12 |
12 |
12 |
11 |
11 |
12 |
12 |
2 |
13 |
15 |
15 |
15 |
13 |
13 |
13 |
13 |
14 |
13 |
|
3 |
12 |
13 |
12 |
13 |
13 |
11 |
8 |
8 |
8 |
9 |
3 |
13 |
15 |
14 |
14 |
14 |
13 |
7 |
7 |
7 |
7 |
|
4 |
12 |
13 |
12 |
13 |
8 |
7 |
7 |
7 |
7 |
8 |
4 |
14 |
15 |
14 |
14 |
7 |
6 |
6 |
6 |
6 |
7 |
|
5 |
11 |
12 |
12 |
11 |
7 |
7 |
7 |
8 |
8 |
8 |
5 |
12 |
15 |
13 |
13 |
6 |
6 |
6 |
7 |
7 |
7 |
|
6 |
11 |
12 |
12 |
12 |
8 |
8 |
7 |
7 |
8 |
9 |
6 |
12 |
13 |
13 |
13 |
7 |
6 |
6 |
6 |
7 |
8 |
|
7 |
12 |
12 |
12 |
12 |
8 |
7 |
7 |
7 |
7 |
8 |
7 |
13 |
13 |
13 |
13 |
6 |
6 |
5 |
5 |
6 |
6 |
|
8 |
11 |
13 |
13 |
12 |
8 |
7 |
7 |
7 |
7 |
8 |
8 |
14 |
15 |
15 |
14 |
6 |
6 |
5 |
5 |
6 |
6 |
|
9 |
11 |
12 |
12 |
12 |
11 |
8 |
7 |
7 |
8 |
8 |
9 |
13 |
15 |
15 |
14 |
12 |
6 |
5 |
5 |
6 |
6 |
|
10 |
8 |
8 |
9 |
9 |
9 |
8 |
8 |
8 |
8 |
7 |
10 |
6 |
7 |
8 |
8 |
9 |
6 |
6 |
6 |
6 |
6 |
|
2a. SAF- Replication #9. |
2b. WSAF - Replication #9. |
||||||||||||||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
||
|
1 |
12 |
12 |
12 |
12 |
12 |
11 |
11 |
12 |
12 |
12 |
1 |
13 |
13 |
12 |
13 |
13 |
12 |
12 |
13 |
13 |
13 |
|
2 |
12 |
11 |
12 |
12 |
12 |
12 |
10 |
10 |
11 |
12 |
2 |
13 |
12 |
12 |
14 |
12 |
12 |
10 |
10 |
13 |
13 |
|
3 |
12 |
12 |
12 |
12 |
11 |
10 |
8 |
8 |
8 |
8 |
3 |
13 |
12 |
13 |
14 |
12 |
11 |
7 |
7 |
7 |
7 |
|
4 |
11 |
12 |
12 |
12 |
8 |
7 |
7 |
7 |
7 |
8 |
4 |
12 |
12 |
12 |
13 |
6 |
6 |
6 |
7 |
7 |
7 |
|
5 |
12 |
13 |
12 |
12 |
8 |
7 |
7 |
7 |
7 |
8 |
5 |
13 |
14 |
12 |
13 |
6 |
6 |
6 |
6 |
7 |
7 |
|
6 |
11 |
12 |
12 |
12 |
9 |
6 |
7 |
7 |
7 |
8 |
6 |
13 |
13 |
13 |
13 |
8 |
6 |
7 |
7 |
7 |
6 |
|
7 |
11 |
11 |
11 |
11 |
7 |
7 |
7 |
7 |
7 |
7 |
7 |
12 |
12 |
12 |
13 |
7 |
6 |
6 |
6 |
6 |
6 |
|
8 |
10 |
11 |
11 |
11 |
8 |
7 |
7 |
7 |
7 |
7 |
8 |
12 |
12 |
12 |
12 |
7 |
7 |
6 |
6 |
6 |
6 |
|
9 |
10 |
10 |
11 |
10 |
9 |
7 |
7 |
6 |
6 |
7 |
9 |
12 |
12 |
12 |
12 |
12 |
7 |
6 |
6 |
6 |
6 |
|
10 |
8 |
8 |
8 |
7 |
8 |
6 |
5 |
6 |
6 |
6 |
10 |
8 |
8 |
8 |
8 |
7 |
5 |
5 |
6 |
6 |
5 |
|
2c. SAF - Replication #10. |
2d. WSAF - Replication #10. |
||||||||||||||||||||
|
Figure 4.2 SAF and WSAF Estimates for the Intercept Parameter of the Step Jump in Intercept Case - 2 Replications |
|||||||||||||||||||||
Figure 4.2 shows estimated b 0 parameter maps for two replications of the step jump case. Panels a and b are SAF and WSAF estimates respectively for a replication that we classified as having a good fit. Panels c and d are a "poor" fit replication. While both versions of SAF detect the step jump in the intercept, WSAF improves the contrast around the border. In particular, the WSAF estimates for the "enclave" and the thin strip of "territory" at the bottom of the maps are far better. The SAF estimates tend to smooth out the step jump.
911 Drug Calls
per 1000 Population
|
400 +
| A
|
|
|
300 +
|
|
|
|
200 + AA
| A
|
| A
| A
100 + A A
| A A B
| A A B
| A A A AA A A BA AA
|AB AAA A A B A AA AA A A BAAAC
0 +LZMJKFCCDA A A C AA AAA A A A A A
À +---------+---------+---------+---------+---------+--
0 20 40 60 80 100
Percentage Black Population
Figure 4.3: Plot of 911 Drug Nature Code Calls per Capita versus Percentage Black Population (1991 in Pittsburgh, by Census Tract). A = 1 Obs., b = 2 Obs., etc.
The case study of this section is on street-level, illicit drug markets. These markets, at the bottom of the supply chain, involve direct transaction between drug dealers and users. The primary indicator of street-level drug dealing are 911 emergency call-for-service data. All calls to Pittsburgh's computerized 911 system are classified into nature codes. The drug nature code covers a wide range of perceived drug dealing activities by citizen callers. Sherman, Gartin and Buerger (1989) make the case for using police 911 emergency call-for-service data in studying crime patterns. Such data are particularly useful indicators for the case study of this chapter, since drug dealing is a victimless crime. Victims of burglaries, etc., notify police, resulting in the creation of official reports. Drug offenses, of course, are not reported in this fashion.
Building on an ecological theory of crime by Cohen and Felson (1979), Sherman, Gartin and Buerger (1989) demonstrated empirically that predatory crimes (robberies, rapes and auto thefts) occur at relatively few "hot spots" (points) in a metropolitan area. These researchers, however, did not attempt to determine boundaries circumscribing clusters of hot spots as did Spring and Block (1988) (reported in Roncek and Baier, 1991).
While not predatory crimes, drug sales and use apparently are also limited to relatively few hot spot points and areas. A written questionnaire and interviews with narcotics officers of the Pittsburgh Bureau of Police identified roughly 125 drug dealing hot spots - including street corners, bars, and other points - located in eleven drug market areas encompassing 19 percent (33 out of 174) of the census tracts in Pittsburgh. Drugs dealt include primarily crack and powdered cocaine and heroin.
Two out of the eleven Pittsburgh drug-market areas are primarily white in racial composition (having around the city-wide average of 26 percent black population). These markets tend to be close-knit, with dealing only between dealers and buyers known to each other. Open street-level drug dealing in Pittsburgh occurs primarily in census tracts or neighborhoods with high proportions of black population. Note that poverty, and not race, is the primary cause of spatial crime clusters (for example, Shaw, 1929; Schmid, 1960; Dunn, 1980). In other cities, poor whites, Hispanics, Asians, etc. are in drug hot spots. Note further that the greater number of black neighborhoods are not drug market areas. This can be seen in figure 4.3 which is a scatter plot of census tract level data for Pittsburgh in 1991 of total 911 drug-nature code calls per thousand population versus percentage black population. Sixty-one percent (22 out of 36) of the census tracts having 60 percent or more black population have drug dealing levels below fifty calls per thousand population. Fifty calls per thousand population per year or less is characteristic of the entire racial spectrum in Pittsburgh.
Figure 4.4 shown in Appendix C is a choropleth map of Pittsburgh census tracts showing 1991 total 911 drug-nature calls per thousand population and the drug market area boundaries determined from questionnaires and interviews with narcotics officers. Figure 4.5 in Appendix C shows percentage black population using a geometric growth scale to emphasize dispersion around the mean of 26 percent. A comparison of Figures 4.4 and 4.5 further makes the point that open street-level markets tend to be in heavily black population areas; however, not all black census tracts are drug market areas. Evidently, a model relating 911 drug nature code data to variables like percentage black population should have discrete spatial changes in certain parameters, with sharp increases in drug market areas.
An aim in our drug-market modeling research is to expand a model using offender and neighborhood socioeconomic characteristics (like percentage black, education levels, income, percent of female households, etc.) to include spatial considerations. Most relevant socioeconomic variables tend to be highly correlated with percentage black population, so as an expansion modeling step we apply SAF and WSAF to a simple linear model relating 911 drug calls per thousand population to an intercept and a term for percentage black population. The options for specifying spatially varying parameters included making both the intercept and coefficient of percentage black population varying, or either varying and the other constant. Ws estimated all three options but only display estimated parameter maps for the simple case with the varying intercept and coefficient of percentage black constant (its initial value). The model with both parameters varying fits the data better; however, the simpler model chosen illustrates the difference between SAF and WSAF more clearly.
Initial values for SAF and WSAF were determined by applying OLS to the data displayed in Figure 4.3, resulting in an intercept of 17 and a slope of 72. Initial runs of SAF and WSAF indicated that census tracts with small populations, especially industrial sites, along rivers, were inappropriately dominating estimates. Therefore, all census tracts with populations less than 550 were excluded by disconnecting them from the contiguity matrix for Pittsburgh census tracts.
Figures 4.6 and 4.7 in Appendix C are plots of estimated spatially varying intercepts made by SAF and WSAF respectively. The optimal damping factors for SAF is 0.9, the maximum permitted in the grid search for this parameter. Nevertheless, SAF was barely able to estimate the spatial variation as compared to WSAF. WSAF had a slightly lesser optimal damping factor of 0.8, but nevertheless estimated much more spatial variation. Table 4.3 presents performance measures for the initial regression model, the spatially varying model depicted in Figures 4.6 and 4.7, and the two other spatially varying parameter models. SAF appears to perform as well or slightly better than WSAF overall; however, WSAF has much greater variation in estimated coefficients. When there are several contiguous census tracts with high drug call values, WSAF tends to smooth the intercept for such tracts so that estimated dependent variables have both positive and negative residuals.
|
Table 4.3 Performance of OLS Regression and Three Spatially Varying Parameter Models for 911 Drug Calls versus Percentage Black Population |
||||||
|
Spatial MAPE |
Spatial MPE |
Intercept Damping Factor |
Slope Damping Factor |
Range in Estimated Intercept |
Range in Estimated Slope |
|
|
OLS Varying Intercept |
38.1 |
-37.8 |
N/A |
N/A |
N/A |
N/A |
|
SAF |
10.7 |
-10.0 |
0.9 |
N/A |
13.5 |
N/A |
|
WSAF |
10.0 |
-9.2 |
0.8 |
N/A |
74.8 |
N/A |
|
Varying Slope |
||||||
|
SAF |
28.7 |
-28.0 |
N/A |
0.9 |
N/A |
57.6 |
|
WSAF |
28.8 |
-28.2 |
N/A |
0.4 |
N/A |
279.7 |
|
Varying Intercept and Slope |
||||||
|
SAF |
4.9 |
-3.5 |
0.9 |
0.8 |
16.9 |
60.5 |
|
WSAF |
5.4 |
-4.3 |
0.1 |
0.2 |
21.2 |
131.9 |
Substantively, the estimated parameter map in Figure 4.7 suggests some possibilities for model expansion. First, isolated public housing developments appear to be modeled sufficiently well using percentage black population (compare Figures 4.5 and 4.7). This result makes sense as the housing developments are homogenous in land use (housing only) and socioeconomic factors (poverty and blacks). Second, most of the drug market areas with a mix of land uses apparently have additional factors causing more 911 drug calls than predicted by the initial OLS model. We suspect, along the lines suggested by an ecological theory of crime (see Cohen and Felson, 1979, and Roncek and Maier, 1991), that certain land uses and structures attract drug dealing. The presence of bars and run-down commercial areas are factors that we are now pursuing in an expanded model.
Lastly, Figure 4.7 makes it evident that WSAF is readily capable of representing multiple maxima and minima in spatially varying parameter estimates. Polynomial trend surface expansions have only limited ability for such representation. Fourier polynomial trend surfaces based on Varimax rotated principal components of spatial polynomial variables are much more able to estimate such surfaces (see Casetti and Fan, 1991).
This chapter has introduced a new pattern recognizer for automatically weighting multiple feedback signals used in SAF. These signals are applied iteratively to estimate the spatially varying parameters of cross-sectional multivariate models. The weighting scheme uses inverse spatial forecast errors made from neighboring observation points to the point undergoing revision, and is able to discriminate relevant versus inappropriate sources of feedback. The Monte Carlo study of this chapter has demonstrated that the resultant WSAF method estimates spatially varying parameters as well as SAF for cases with sharply changing or discontinuous parameters. A case study on modeling illicit drug-market behavior has further supported these conclusions.
Besides handling contiguity-based feedback and abrupt spatial parameter variations, other kinds of feedback may be able to be incorporated into adaptive filters using the pattern recognizer. Examples include hierarchical influences from distant points and temporal influences from past data points in cross-sectionally pooled time series data. For example, Peter Gould and Joe Kabel, using a Cray supercomputer ate Penn State University, have applied WSAF to predicting the spatial diffusion of AIDS incidence using quarterly, county-level data over a ten-year period and the continental United States (Kabel, 1992). They applied WSAF separately to each cross section of data and made time series extrapolations of varying parameters. Included in this research was an approach using the pattern recognizer weighting scheme to automatically identify hierarchical diffusion linkages.
Our future work on adaptive filtering includes the development and testing of an extension of WSAF for pooled space and time series data, incorporation of artificial neural network types of nonlinear functional forms, and application of randomization methods for developing significance tests.
5. Chaos Theory, Artificial Neural Networks and GIS-Based Data: Chaotic Cellular Forecasting and Application to the Prediction of Drug Related Call for Service Data
The problem of forecasting space-time phenomena is one that has occupied geographers for decades. Complicating the search for accurate and robust forecasting models is the fact that space-time phenomena more often than not exhibit behavior inconsistent with that assumed by modern statistical theory. For example, the spatio-temporal distributions of some types of criminal activity appearing chaotic or almost random in nature are often non-linear and discontinuous across space and time. Model heterogeneity is especially true for criminal activity such as street level drug dealing, which is difficult to model at the microlevel of census tracts or smaller units.
Geographers and Regional Scientists have long realized that local context and spatial heterogeneity are extremely important when forecasting space-time phenomena (see for example Anselin, 1988), and have consequently devised a number of ways in which to do so (see for example Cliff et al, 1975). Some of these methodologies have been applied to modeling and forecasting spatial patterns of criminal behavior (see for example Dunn, 1980; Gorr and Olligschlaeger, 1994), albeit with varying degrees of success. Nevertheless, difficulties in obtaining high quality localized data and building successful models have yielded only few examples in the literature that employ spatio-temporal forecasting techniques to crime patterns.
Over the past five years, however, the use of geographic information systems (GIS) in police departments across the country has increased considerably (Maltz, 1993 and McEwen and Taxman, 1994). In addition, some police agencies have begun to integrate GIS with other sources of data such as 911 calls for service and police records management systems. This has resulted in the availability of high quality data at the address, or point level. Consequently data can be aggregated according to any desired spatial unit or grid system while still preserving all other attributes related to that point, thus producing very accurate spatio-temporal data sets.
This paper introduces a new spatio-temporal forecasting methodology that combines artificial neural networks and cellular automata with GIS-based data. The technique, which we refer to as chaotic cellular forecasting (CCF) is similar to spatial adaptive filtering due to Foster and Gorr (1986) and weighted spatial adaptive filtering due to Gorr and Olligschlaeger (1994) in that it uses contiguity relationships and the geographer's assumption that influence between data points decays with distance. As with spatial adaptive filtering the methodology uses an iterative process to arrive at a solution. Unlike spatial adaptive filtering, however, chaotic forecasting uses a gradient descent method rather than a grid search to find the optimal set of parameters (or, in the case of artificial neural networks, weights). In addition, and most importantly, CCF has a nonlinear functional form commonly used in neural net modeling, allowing for increased pattern recognition and accommodation of spatio-temporal heterogeneity. The result is a robust spatio-temporal forecasting method that requires very little model specification, is self adapting and performs very well on data sets that exhibit non-traditional statistical behavior.
The second section in this paper briefly reviews the spatially varying parameter model and the literature on spatio-temporal forecasting. The third section outlines the chaotic cellular forecasting method and illustrates how it was derived from cellular automata and a particular type of artificial neural network: a multilayer feedforward network with backpropagation. The fourth section describes a comparative study of chaotic cellular forecasting with a number of traditional spatial forecasting techniques using GIS-based data derived from the Pittsburgh Drug Market Analysis Program (DMAP). Holdout samples in a rolling forecast design over 12 months are used to determine the out-of-sample forecast accuracy of each method. The fifth section reviews the results and last section provides a brief summary and conclusion.
5.2 Spatial Forecasting Methods and Models
According to Anselin (1988) there is much evidence of the model heterogeneity over spatial context. He argues that modeling strategies should take into account features unique to each location or spatial unit. In the absence of a completely specified model over space and time, researchers must resort to a model that accommodates spatio-temporal heterogeneity using varying parameters:
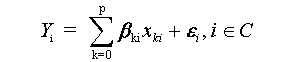
where C is an index for the space-time context of parameter variation, i is an index in C denoting place and time, Yi is the independent variable at observation i, b ik is the parameter for the kth independent variable for observation i (k = 0,1,2...p), and e i is the error term for observation i. Implementing this model in unconstrained form is impossible because the number of parameters is p+1 times the number of observations. Consequently researchers have devised a number of strategies to counter this problem by constraining variation of the b ik over C (e.g., Anselin, 1988; Gorr and Olligschlaeger, 1994).
Classical econometric fixed and random effects models (see Cliff et al, 1975) contextuate via dummy variables, assuming that effects of space and/or time are fixed. These types of models are most often used in situations where the number of observations is limited and spatio-temporal heterogeneity is viewed strictly as a nuisance in estimating the non-varying parameters that hold across space and time. Those methods have the goal of estimating behavior which is constant over space and time while controlling or screening out varying behavior.
Two methods which explicitly model heterogeneity for use in exploration and forecasting are locally weighted regression (see for example Cassetti, 1982, and Cleveland and Devlin, 1988) and Kriging (David, 1977; Haining, 1990). Locally weighted regression techniques require that the weights determining spatial variation be specified a priori via trial and error. Kriging, or in the multivariate case, co-kriging, use an empirically estimated function, called the variogram, to determine the spatial weighting of data observations. Both methods assume that the influence of other observations declines with distance from the current observation.
Model (5.1) is also often used in exploratory data analysis (see for example Bretschneider and Gorr, 1983). Maps of residuals can show undetected heterogeneity suggesting additional theory or model structure, and maps of estimated spatially varying parameters are useful in determining the functional form of parameter variation. A similar type of exploratory data analysis is expansion modeling, e.g. step-wise regression models using polynomial or other functions of time and space coordinates which interact with an initial model's variables (Cassetti, 1986 and Cassetti and Jones, 1992).
A non-causal modeling or "naïve" approach to accommodating heterogeneity uses spatial and temporal lags of variables or model residuals. A univariate example is the Space-Time Autoregressive model, or STAR (Tobler, 1969) which is an extension of the purely temporal autoregressive model due to Box and Jenkins (1970) and assumes that the influence of neighboring observations declines with distance from the current observation according to a set of predefined spatial weights. Other examples include the Space-Time Autoregressive Integrated Moving Average (STARIMA) model which incorporates repeated differencing for trend elimination and the exponential smoothing model (Cliff et al, 1975).
Still another approach uses pattern recognition with the geographer's assumption of distance decay for influence, and shares a heredity that also led to neural network models. Two such methods are spatial adaptive filtering (SAF) and weighted spatial adaptive filtering (WSAF), both of which are based on adaptive filtering due to Widrow and Hoff (1960). Neural network model estimation also draws upon adaptive filtering. Foster and Gorr (1986) introduced SAF as an extension of multivariate damped negative feedback estimation for pattern recognition by using a grid search approach to optimizing individual damping factors for each b k in model (5.1). WSAF was introduced by Gorr and Olligschlaeger (1994) as an extension of SAF. It incorporates an additional pattern recognizer component into SAF that reduces an inherent bias due to applying equal weights to feedback signals from neighboring observations and allows for self-modeling of spatial discontinuities. Based on the magnitude of forecast errors using the b k of neighboring observations WSAF automatically assigns appropriate weights to feedback signals: those observations with small forecast errors receive relatively large weights, whereas those with larger errors receive smaller weights. The resulting weighting scheme is similar to those used in time-series combination forecasting (see for example Bates and Granger, 1969, and Clemen, 1989).
The idea of using artificial neural networks (ANNs) for forecasting is relatively new. While ANNs have been the subject of intense research efforts over the past decade, yielding many technological advances in areas such as robotics, speech recognition and the detection of explosives, it was not until White (1988) used ANNs to predict IBM daily stock returns that they were first used to forecast temporal patterns of economic behavior. Nevertheless there have been no examples in the domain of spatio-temporal forecasting (see Sharda and Patil, 1990, and Tang et al, 1990, for one of the few exceptions). To the best of our knowledge no ANN-based spatio-temporal forecasting models have been developed to date.
There are many different types of artificial neural networks. Since even a cursory introduction is far beyond the scope of this paper the interested reader is referred to Rumelhart and McClelland (1988) or Kroese and Van der Smagt (1993) for an introduction. The most widely used and studied type of ANN is the multi-layer feedforward network with backpropagation. This type of ANN is a nonlinear extension of Minsky and Papert's (1969) Perceptrons and the same type of network used by White (1988) in temporal forecasting and in CCF introduced in this paper. ANN's have a number of features which make them attractive as candidates for spatio-temporal forecasting. First, they have a flexible, self-adaptive nonlinear functional form which precludes the necessity of determining a priori the specific functional form of the relationship between dependent and independent variables. Second, unlike SAF and WSAF, among other methods, ANN's do not require that parameters be initialized with regression estimates. Rather, the parameters (or weights) are initialized randomly. Finally, Hornik et al (1989) proved that certain ANN's with logistic activation functions and hidden layer architectures form a class of universal approximators, i.e., they can estimate any functional form to any desired degree of accuracy provided sufficiently many hidden units are available. In addition, Lapedes and Farber (1987) have provided evidence that for chaotic time series artificial neural networks can forecast more accurately than conventional methods.
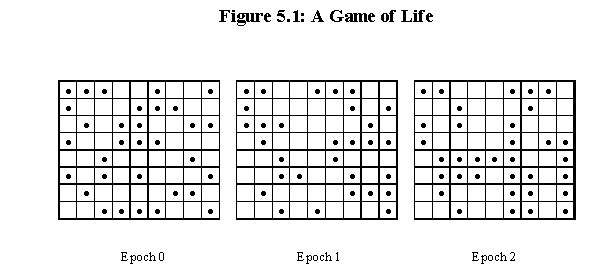
Chaos theory is derived from quantum mechanics and involves the study of phenomena or systems which are very sensitive to initial conditions (for a detailed introduction to chaos theory see Schroeder, 1991). A classical example of a chaotic system is the Mandelbrot set which is frequently used in artwork and as an illustration of how to graphically display complex mathematical functions. Some real world examples include weather patterns, stock market activity and brain activity. One of the fundamental tenets of chaos theory is that although chaotic systems seem to display totally random and unpredictable behavior they actually follow strict mathematical rules which can be derived and studied (Pickover, 1990). These rules can range in sophistication from simple decision trees to complex nonlinear functions.
5.3 Chaotic Cellular Forecasting
Cellular automata are a specific type of chaotic system. They differ from other chaotic systems in that they act on discrete space, or grids rather than a continuous medium such as a surface. In cellular automata machines, each time frame is represented by a layer of cells (representing the "population" of cells). The next time frame is derived by replacing the previous layer according to a set of rules (Toffoli and Margolus, 1987). A key determinant of cellular automata rules is how each cell is influenced by neighboring cells.
Figure 5.1 shows three epochs (time frames) in the life of a population of cells occupying a nine by nine grid. An empty square represents a dead cell, whereas a dotted square represents a live cell. Upon initial examination of the three epochs it appears that cells are born and die randomly. However, this is not the case. The behavior of the cell population from one epoch to the other actually follows a very simple set of rules introduced by mathematician John Conway in his game of life (Gardner, 1970). Assuming that the neighborhood of a cell consists of all immediately adjacent or touching cells (Queen's case) the rules are as follows:
Note that the rules for the game of life do not vary spatially, i.e., the same rules apply to each cell in the population regardless of its location. Nevertheless, the rules result in various spatial patterns. A further important observation in this regard is that the rules produce one step ahead forecasts of cell populations.
Spatial phenomena often exhibit the same kind of apparently random and chaotic behavior as the cells in the game of life described above. For example, if we were to divide space into cells and count the number of infected individuals per cell per time frame, then it is quite possible that over time cells would display similar seemingly unpredictable behavior as in the game of life, even though the rules of infection are quite simple. In other words it is conceivable that some spatio-temporal phenomena are actually the result of chaotic systems. Even minute changes in the parameters of cellular automata machines can result in a changeover from long term stability to short term chaotic behavior within the cell population (Schroeder, 1991).
This could help explain, for example, why spatial patterns of criminal activity have begun to defy conventional theory in recent years. For example, it is possible to draw some analogies between the rules of the game of life and the behavior of street level drug markets. A drug market in a cell could "die" if there is overcrowding in its neighborhood, i.e., there are too many drug dealers, which either invites police intervention or leads to turf wars. On the other hand, one active drug market cell in an area where there are otherwise none would result in its being too inconspicuous. Finally, for an area to become a place of drug dealing certain conditions must be met. The analogy between rule number two could be that there must be displacement or spillover from neighboring drug markets.
The rules of the game of life are very simple. Rules governing real world chaotic systems are far more complex, however. The problem is that they are only rarely, if ever, known a priori. If for the moment we assume that spatio-temporal patterns are indeed the manifestations of chaotic systems, then many conventional space-time models can be viewed as suggestions for rules. These suggestions are then tested against consecutive populations of cells, census tracts or any other areal unit. Often suggested models, or rules work quite well, sometimes they do not. Chaotic cellular forecasting (CCF) is essentially a cellular automata machine that works in reverse: instead of applying the rules or testing suggested rules it attempts to learn them. However, as will be illustrated, CCF still requires some experimentation with different network parameters.
The mechanism used for learning the rules are feedforward networks with backpropagation. This type of artificial neural network lends itself best to the problem at hand for a number of reasons. First, backpropagation networks have been used successfully elsewhere for time series forecasting (see White, 1988; Poli and Jones, 1994). Second, backpropagation networks are capable of estimating extremely complex functions (input to output mappings) without the necessity of specifying a priori the functional form. Finally, the gradient descent method used to minimize the total sum of squared errors is not prone to converging to local minima on the error surface (Weiss and Kulikowski, 1991). The rest of this section describes chaotic cellular forecasting in more detail using the game of life as an example.
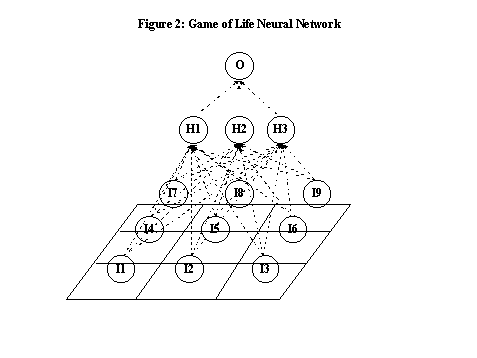
Figure 5.2 shows how CCF was used to estimate the rules of the game of life. The network consists of three layers: the input layer, 3 hidden units and the output layer. The number of input units in CCF is determined by the neighborhood of a cell as well as the number of signals (or inputs) each cell sends to the hidden layer (this is analogous to the number of independent variables in regression). Since the game of life only considers whether a cell is dead or alive, each cell has only one input unit. The value of the signal is 1 if the cell is alive, and 0 otherwise. The neighborhood in this case consists of nine cells (the Queen's case), consisting of the current observation and the eight cells that it touches upon. We therefore have a total of nine input units. The intermediate, or hidden layer consists of three units. Each of the three hidden units is connected to all input units. Finally, the output unit receives its signal from the hidden layer via three connections.
Each processing unit (or neuron) in a backpropagation network receives input from the units to which it is connected in the layer below. Figure 5.3 shows how these input signals are processed. The total (net) input of a unit is the sum of all signals multiplied by their connection strengths (weights) plus a bias. More formally:
![]() (5.2)
(5.2)
where neti is the net input for processing unit i for input pattern p, wij is the weight of the connection between processing unit i and processing unit j in the previous layer, apj is the activation of unit j in the previous layer and q pi is the bias associated with unit i. The activation function used to process the net input varies, but generally takes on a sigmoid functional form. The most commonly used function is the logistic function. It yields values in the range [0,1] and determines the activation of the processing unit at the next step as follows:
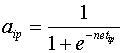 (5.3)
(5.3)
where aip is the activation of unit i for input pattern p. For input units the activation is usually equal to the net input since only one signal needs to be processed.
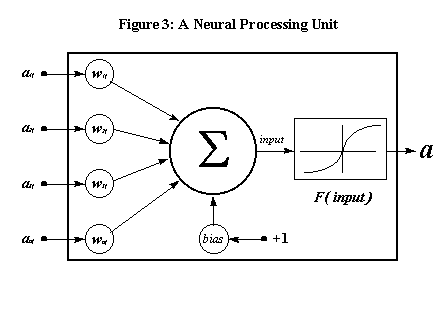
The goal in feedforward networks is to map the input units to a desired output similar to the way in which the dependent variable is a function of the independent variables in regression analysis. The difference is that regression uses direct linear models whereas multi-layer feedforward networks use indirect nonlinear models. The hidden layer creates an internal representation of the patterns to be modeled. This internal representation is then mapped to the output unit. It is the hidden layer, along with the use of a nonlinear activation function that allows multi-layer networks to map far more complex functions than simple direct input to output unit mappings.
Feedforward networks with backpropagation "learn" to map the input units to the output units by adjusting the weights on the connections in response to error signals transmitted back through the network. This is the ANN equivalent of model estimation. During training the network is presented with each input pattern and computes the activation of the output unit(s) using the current network weight structure (the weights are initialized randomly prior to training). The difference between the output of the network and the target mapping constitutes the error signal. This signal is then propagated back through the network via the processing units and their connections and the weights are updated. The goal is to continually update the weights until the sum of all error signals is minimized.
In backpropagation networks the weights are estimated using the generalized delta rule derived by Rumelhart et al (1988) from the Perceptron convergence procedure due to Minsky and Papert (1969), which in turn is a variation of the delta rule proposed by Widrow and Hoff (1960). The generalized delta rule can be summarized in three equations (for a formal derivation of the generalized delta rule see Kroese and Van der Smagt, 1993 or Rumelhart et al., 1988). The first specifies that the weight change should be proportional to the product of the error signal sent to a receiving unit along a connection and the activation of the sending unit. More formally,
![]() (5.4)
(5.4)
where D pwij is weight change for training pattern p and the connection between processing units i and j, d pj is the error signal sent to unit j, api is the activation of unit i for input pattern p and h is the "learning rate". The learning rate is usually a small number less than 1 and close to zero. The definition of the error signal differs between output units and hidden units. For output units using a logistic activation function it is defined as
![]() (5.5)
(5.5)
where tpj is the target activation for the output unit. For hidden units the error signal is given by
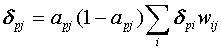 (5.6)
(5.6)
The generalized delta rule implements a gradient descent in the error term. Training of the network proceeds by repeatedly presenting all input patterns and adjusting the weights until the sum of all errors is minimized, i.e. the network converges to a solution. In this respect it is crucial to select a learning rate that during training will allow the network to iterate towards a true global minimum rather than getting stuck in local minima. Learning rates that are too large can lead to oscillations between local minima, whereas small learning rates can require hundreds of thousands of iterations to converge. While it is theoretically possible that even with small learning rates the network will converge to a local minimum, empirical evidence suggests that this is rarely the case (Weiss and Kulikowski, 1991). One way to detect and avoid convergence to local optima is to train the network several times with different random initializations of the weights and to compare the results (Rumelhart et al, 1988).
CCF uses batch processing to adjust connection weights. Rather than adjusting the weights after each input pattern (or observation and time period), weight changes are summed over all input patterns (observations and time periods). After all observations have been processed, the sum of changes is divided by the number of observations multiplied by the number of time periods (which is equal to the number of input to output mappings) to arrive at a "smoothed" weight change for each connection. Experimentation has shown that updating weights in this manner yields better results and leads to faster convergence (Rumelhart et al, 1988).
The data for CCF is obtained by superimposing a regular grid on the study area and aggregating data values for the independent variables for each time period and grid cell. In the game of life the only data point per grid cell and time period consists of whether the cell is dead or alive. In CCF an example of a data point might be the number of burglary arrests per time period in a grid cell. A further example would be the proportion of housing units in the cell that are abandoned or tax delinquent during a time period.
The neighborhood used to produce one-step-ahead forecasts in CCF consists of the current observation (cell) and the eight surrounding cells. As in Figure 5.2 each hidden unit is connected to each grid cell in the neighborhood. The difference is there are multiple connections to each grid cell because multiple signals (independent variables) are processed. This produces spatially and, because the network produces one-step-ahead forecasts, also temporally lagged data points.
The algorithm for training the CCF network using spatially and temporally constant weights for all connections and a single hidden layer is therefore as follows:
For each input to hidden unit connection:
- randomly initialize the weight
For each hidden to output unit connection:
- randomly initialize the weight
Begin iteration
For each input to hidden unit connection:
- set the sum of weight changes to zero
For each hidden to output unit connection:
- set the sum of weight changes to zero
1. Produce one-step-ahead forecasts for all grid cells:
For each time period:
For each grid cell:
1. Forward pass:
- for each hidden unit:
- calculate the net input using signals (data) from the current
grid cell as well as those in the neighborhood (spatially lagged
variables)
- calculate the hidden unit activation
- calculate the output of the network; this is the
estimated forecast
2. Backward pass:
- calculate the forecast error (actual - forecast)
- for each connection (input to hidden and hidden to output)
calculate the weight change and add it to the sum of weight changes
for that connection over all forecasts
- calculate the squared forecast error and add it to the sum of
squared forecast errors
2. Batch update of network weights.
For each input to hidden unit connection:
- divide the total weight change (sum of all weight adjustments) by the
number of observations multiplied by the number of time periods; this is
the average weight change
- adjust the weight by the average weight change
For each hidden to output unit connection:
- divide the total weight change (sum of all weight adjustments) by the
number of grid cells multiplied by the number of time periods; this is
the average weight change
- adjust the weight by the average weight change
If the total sum of squared forecast errors in the current iteration is greater than or equal to that of the previous iteration, stop. Otherwise, continue iterating.
End Iteration.
A second CCF algorithm relaxes the spatially constant weight assumption in that each observation has its own unique set of input to hidden unit connections and associated weights for each cell in the neighborhood. However, the hidden to output unit weights are spatially constant. This produces a hybrid model that has the advantage of some spatial variation in the weight structure but not too much to cause overfitting. However, using a varying weight structure, even in a hybrid model as described above, requires a very large number of observations. As will be outlined below, this potential problem is overcome via the use of GIS based data.
The algorithm for this hybrid CCF model, which assumes temporally constant but spatially varying input to hidden unit weights and a single layer of hidden units is therefore:
For each grid cell:
For each input to hidden unit connection:
- randomly initialize the weight
For each hidden to output unit connection:
- randomly initialize the weight
Begin Iteration
For each grid cell:
For each input to hidden unit connection:
- set the sum of weight changes to zero
For each hidden to output unit connection:
- set the sum of weight changes to zero
1. Produce One-Step-Ahead Forecasts for all Spatial Units:
For each time period in the data set:
For each grid cell:
1. Forward Pass:
- for each hidden unit:
- calculate the net input using signals (data) from the current
grid cell as well as those in the neighborhood (spatially lagged
variables) and input to hidden layer weights associated with the
current grid cell
- calculate the hidden unit activation
- calculate the output of the network; this is the
estimated forecast
2. Backward Pass:
- calculate the forecast error (actual - forecast)
- for each connection (input to hidden and hidden to output)
calculate the weight change and add it to the sum of weight changes
for that connection and grid cell over all forecasts
- calculate the squared forecast error and add it to the sum of
squared forecast errors for the current grid cell and connection
2. Batch Update of Network Weights.
For each grid cell:
For each input to hidden unit connection:
- divide the total weight change (sum of all weight adjustments) by
the number of time periods; this is the average weight change
- adjust the weight by the average weight change
For each hidden to output unit connection:
- divide the total weight change (sum of all weight adjustments) by the
number of observations multiplied by the number of time periods; this is
the average weight change
- adjust the weight by the average weight change
If the total sum of squared forecast errors in the current iteration is greater than or equal to that of the previous iteration, stop. Otherwise, continue iterating.
End Iteration.
When calculating the input values of the neighborhood of an observation a boundary problem arises. This is similar to other spatial forecasting methods. In the Queen's case, for example the boundary problem is caused by the fact that cells bordering the edge of the study area do not all have eight neighbors. In the game of life, for instance, cells at the corners of the grid only have three neighbors. In the case of irregularly shaped grids, such as that of a city, it is possible that some cells have only one neighbor. Since backpropagation networks require that all input to output mappings have the same number of input units, CCF tackles this problem by assigning "imaginary" neighbors to border cells. The inputs of the imaginary cells are set to zero, which means that no weight adjustments will take place along connections to "imaginary" neighbors. While this still introduces some bias it is at least assured that the number of input units is consistent.
A drawback of backpropagation networks and, by extension, CCF is that they require a very large number of observations for training. Backpropagation networks can very easily "memorize", or overfit the data. This occurs not only when the number of observations is too small, but also when the number of connections is too large. The problem is analogous to having too many parameters in regression, resulting in not enough degrees of freedom. CCF requires a relatively large number of connections due to the number of observations in the neighborhood. The varying weight CCF model outlined below requires even more connections. This increases the danger of overfitting the data. Our solution to the problem, outlined below in more detail, is to increase the number of observations using the capabilities of geographic information systems.
As one of the first tests of the algorithm CCF was used to estimate the rules of the game of life using the network shown in Figure 5.2. Presenting all of the results would go beyond the scope of this paper. Suffice it to say, however, that the network was able to learn the rules of the Game of Life perfectly, i.e., without error. Moreover, the network performed flawlessly even when shown patterns that were not used during training: different random initializations of the grid cells had no effect on the performance of the network. In addition, it was able to predict successive generations of cells ad infinitum, requiring only the first epoch of randomly initialized cells to do so. This indicates that the network is robust and able to generalize well, at least for this particular problem.
As mentioned earlier, real life chaotic systems are far more complex than the Game of Life. In addition, most real world systems have an element of randomness, i.e., even if the rules are known there will always be a random error term. Thus it is unreasonable to expect CCF to perform as flawlessly on real world problems. However, given the unique functional form and robustness of backpropagation networks as well as their ability to estimate very complex functions it is reasonable to expect CCF to perform at least as well as some of the traditional spatial forecasting techniques.
A further drawback of backpropagation networks is that much experimentation with the network architecture is sometimes required before an optimal solution can be found. This was also the case with early experiments on the data used in this chapter. In particular it was found that the network described in Figure 5.2 would overfit the data using as few as three hidden units, despite the fact that over ten thousand data points were used to train the network. This was true both for the spatially constant weight model as well as the hybrid model using spatially varying weights.
Further experimentation revealed that adding direct input to output connections to the network architecture kept overfitting in check, i.e., the network would generalize better. In effect adding direct input to output connections results in a hybrid Backpropagation/Perceptron architecture, with both linear direct and nonlinear indirect input to output mappings. In addition, it was found that averaging spatially lagged variables from the neighborhood of an observation rather than connecting each independent variable in each neighboring grid to each hidden unit (as is the case in Figure 5.2) reduced the number of connections, and, by extension, also the amount of overfitting. In other words, instead of nine sets of inputs, one from each observation in the neighborhood, the architecture only had two sets: one from the current observation, and one for the averaged spatially lagged independent variables of the eight neighboring grid cells. The spatially varying weight version of CCF was chosen to estimate the model outlined in the next section. It was also found that this CCF architecture converged must faster than any other previously tested, on the average 4 times faster.
The following section tests the capabilities of CCF with a model that forecasts drug calls for service using data derived from a geographic information system developed for the City of Pittsburgh police department.
5.4 Forecasting Drug Calls for Service: A Comparison Between Traditional Forecasting Methods and Chaotic Cellular Forecasting
Like many other cities of its size Pittsburgh experienced a marked increase in street level drug dealing during the late 1980's and early 1990's as a result of the crack cocaine epidemic. Although crack cocaine use was already prevalent in larger cities such as Los Angeles, Detroit and New York City before that time, historical evidence shows that it generally takes a few years for new illicit drugs to disperse to smaller cities that are not ports of entry for drug smugglers. Prior to the appearance of crack cocaine street level drug dealing in Pittsburgh was largely confined to two areas which specialized primarily in heroin and marijuana. Other sporadic areas of open air drug dealing did exist, but were mainly limited to the sale of prescription drugs such as painkillers and the "Yuppie" drug powder cocaine.
In the summer of 1991 Pittsburgh also experienced a surge in gang related violence. While initially most gangs in Pittsburgh were merely loosely organized groups of adolescents, experienced gang members from larger cities quickly attempted to gain a foothold in what they perceived as "virgin territory" for crack cocaine sales. Street level drug markets in other major cities were already saturated by dealers and there was little opportunity for entry into a market tightly controlled by gangs. Pittsburgh, on the other hand, was still a "free-for-all": demand was greater than supply. Thus at least a part of the increase in violence can be attributed to street gangs setting up and defending "turfs" within which they plied their illicit drug trade.
In reacting to the increase in street level drug dealing the Pittsburgh Bureau of Police was using disruptive enforcement strategies which were proven highly successful in other cities: reverse stings, undercover buys, on-sight arrests of drug dealers after having observed illicit transactions and placing community oriented police officers in plain view of established drug hot spots. These strategies were used because street-level drug dealing is widely regarded as a weak link in the chain: once a street market has been disrupted it is very difficult for dealers to relocate (Cohen et al., 1993). They are unable to advertise their new location and are severely restricted in establishing new ones because they might infringe upon turfs already claimed by other drug dealers. However, there were a few instances where new hot spots did eventually surface.
Geographic information systems perform quite well when tracking the geographic displacement of drug dealers due to their ability to plot the locations and frequencies of the number of drug calls for service and drug arrests. But they do not perform as well at identifying emerging drug markets. The reason for this is twofold: first, police officers rarely make arrests in areas of which they are unaware that street level drug dealing is going on unless they happen to stumble upon a transaction. Street sweeps tend to concentrate on known drug markets. Second, residents of areas in which street level drug dealing is a relatively new phenomenon frequently are unaware of what is going on. They initially do not perceive the activity as drug dealing (Olligschlaeger, 1997). Rather, they tend to notice an increase in the level of crimes associated with street level drug dealing such as robberies, burglaries and assaults. In addition, violence associated with drug trafficking increases. Thus there is a lag between the time a drug market has established itself and when residents begin to make drug related calls for service.
A forecasting model for the activities of street level drug markets must therefore also be able to predict drugs calls for service based on factors other than simply the level of drug calls for service in previous time periods (such as in a random walk model). Based on the results of previous work and the availability of data from the Pittsburgh Drug Market Analysis Program (DMAP) it was decided to use three types of calls for service as indicators of emerging drug activity: weapon related calls (shots fired, person shot, man with a gun, etc.), robbery calls and assaults. In addition, Cohen et al (1993) showed that ecological factors such as the proportion of commercial properties in an area are important contributors to the level of drug calls for service. Commercial areas (especially older, abandoned ones) lend themselves more to open air drug dealing because of factors such as the relative lack of population outside of regular business hours (there are fewer residents to observe drug dealing). On the other hand, residential areas tend to reduce the amount of street level drug dealing due to increased guardianship of the neighborhood at night and after working hours. Thus the proportion of residential and commercial properties were included as indicator variables. Finally, open air drug dealing is a seasonal phenomenon. In the winter months drug dealers tend to stay inside not only because it is cold, but also because fewer people in general are on the streets and they become more visible. A seasonality index was therefore also included.
One additional independent variable that would be desirable to include as a predictor for the number of drug related calls for service is a measure of the impact of policing. In the absence of daily manpower allocation data the only available candidate for such a measure would be the number of drug arrests in an area. Arrest data, however, especially for drug related offenses, are misleading as an indicator of police activity. The reason for this is that many, if not most, drug arrests occur in an area other than the one in which the offense occurred. For example, arrests are often made in residential areas at the homes of suspected drug dealers where there is no other apparent street level drug activity. With the exception of public housing projects, drug dealers rarely ply their trade in the same area where they live. Police officers do not always arrest suspected drug dealers on sight, i.e., as soon as they observe what they believe to be an illegal drug transaction. This is especially true for undercover drug buys. It may take three or more buys until an arrest is made. Even if only one undercover buy is made, there can be a considerable time delay between the drug transaction and an arrest simply because of the time it takes for the crime lab to process the purchased substance and confirm whether it is indeed an illicit drug.
Certainly not all drug arrests are made at the homes of offenders. The point, however, is that many times simply arresting a person on sight can be counterproductive because potentially useful information about the suppliers and coconspirators of the offender can be lost. For that reason police officers often conduct an investigation, the result of which are arrests which may or may not be in the same area as where the offense occurred. Since the data do not provide any insight as to where the original offense occurred in relation to the location of the arrest, it was decided not to include drug arrests as an explanatory variable.
Three forecasting models were estimated using four different methodologies. The first model is a simple regression model using only the current observations' independent variables, i.e., no spatially lagged variables, and produces one-step-ahead (i.e., one month) forecasts for the number of drug related calls for service:
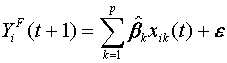 (5.7)
(5.7)
where i is the current observation, YiF is the forecast for observation i, p is the number of independent variables, the b k are the estimated regression parameters, xik(t) are the independent variables for observation i at time t, and e is the error term.
The second model adds spatially lagged variables to model (5.7) above as follows:
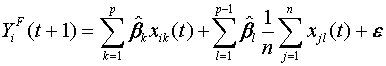 (5.8)
(5.8)
where p is the number of independent variables (in this case it is seven), j represents each observation in the neighborhood, and n is the number of observations in the neighborhood (which is equal to 8 using the Queen's case except in the case of boundary grid cells). The xik represent temporally lagged variables whereas the xj represent spatially and temporally lagged variables. Note that the second part of the equation represents the spatial average of observations in the neighborhood for all variables except the seasonality index. Model (5.8) assumes that the parameters are spatially constant. For the spatially varying parameter case an additional model would be:
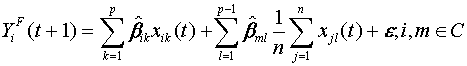 (5.9)
(5.9)
where i and m are indexes in C, the context of spatial parameter variation. The only difference between (5.8) and (5.9) is therefore that in model (5.9) each observation has its own set of parameters. However, this means that model (5.9) cannot be estimated due to the number of parameters. Note that models (5.8) and (5.9) also assume that the dependent variable is a linear function of the independent variables. Feedforward networks with backpropagation do not require this assumption since functional dependencies do not need to be specified a priori.
The chaotic cellular forecasting model can be rewritten in algebraic terms. For the network architecture outlined in the previous section we can write:
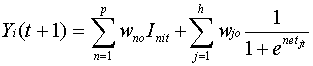 (5.10)
(5.10)
where Yi is the target output of the network for observation i, t is the time period, h is the number of hidden units, p is the number of input units (including the averaged spatially lagged variables), wno is the weight along the direct input to output unit connection between input unit, n and the output unit, o, Init is the input of unit n for observation i at time t, wjo is the weight along the connection between the output unit, o and the hidden unit, j, and netjt is the net input for hidden unit j at time t which is calculated as follows:
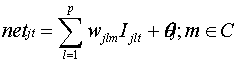 (5.11)
(5.11)
where p is the number of input units per cell in the neighborhood (this is analogous to the number of independent variables) plus the number of averaged spatially lagged variables, Ijlt is the input from unit l at time t for hidden unit j, wjlm is the weight along the connection between hidden unit j and the lth input unit, and q j is the bias for hidden unit j, and m is an index in C, the context of spatial weight variation. In equations (5.10) and (5.11) the weights are the parameters to be estimated.
Note that the output of the network is simply the net input to the output unit. The number of hidden units in this instance of CCF is nine. This number was arrived at using informal experimentation on the data set and does not imply that there should always be nine hidden units in CCF models.
The data for the early warning system were obtained by superimposing a grid on the area of the city of Pittsburgh (see Figure 5.4) and aggregating data for each grid cell and time period (in this case one month). The cells are 2150 feet square (which represents approximately two city blocks), resulting in a total number of 445 cells. In selecting the size of the cells it was important not to make them too small because otherwise only few cells would have more than one or two calls for service. Too large cells would have resulted in too few data points for neural net modeling. Another criterion used in selecting the size of the grid cells was that pin maps of historical drug activity show that the typical drug hot spot area in Pittsburgh is about two city blocks square.
Figure 5.4
Call for service data were obtained by counting the number of calls per month within each cell using the (x,y) coordinates of the geocoded locations. The data spanned the years 1990 to 1992 resulting in 35 months worth of data (December of 1992 could not be used since there was no value for the number of drug related calls for service in January 1993). Future testing and additional modeling will utilize later data. With 445 cells the total number of data points was therefore 15,575. The relative proportions of commercial and residential properties were arrived at by relating property ownership information to parcel polygons via the lot and block number. The (x,y) coordinates of the geographic center of a parcel were then used to determine which grid cell a particular property falls into. The zoning classification for each property provided the basis for the relative frequencies. Finally, the seasonal index was arrived at by assigning values between 0.1 and 0.9 in equal increments to each month, where a value of 0.9 was assigned to June and July and 0.1 to December and January. Since backpropagation networks require a signal from the input units in order for weight adjustment to occur, all variables with a value of zero were adjusted to 0.1. This ensured that connection weights were not adjusted only in the case of non-zero inputs.
Table 5.1 shows the total number of calls for service, by year, for each of the four nature codes used in this study. Notice the remarkable increase in the number of weapon related calls for service of almost 100% over three years. The number of drug and robbery related calls for service also increased. Only assaults showed a decline.
|
Table 5.1: Annual Total Number of Calls for Service |
||||
|
Drugs |
Weapons |
Robberies |
Assaults |
|
|
1990 |
5053 |
3580 |
1922 |
8618 |
|
1991 |
6397 |
4523 |
2309 |
7154 |
|
1992 |
6223 |
6622 |
2699 |
6147 |
Figure 5.6 shows the number of calls for each nature code broken down by month. The seasonal variation is quite noticeable, especially for drugs, weapons and assaults. The figure also shows how, with the exception of assaults, most of the increase in the number of calls for service is accounted for in the summer months.
Models (5.7) and (5.8) were estimated using three different methodologies resulting in six different model estimates. The first methodology is simple regression and the second and third are Poisson regression and Tobit regression, respectively. The Tobit regression model was left censored at 0.1. Equation (5.9) could not be estimated since there are too many parameters for the results to be of any significance. Model (5.10) was estimated using chaotic cellular forecasting. In addition, all results were compared to a simple random walk, i.e., a model where the assumption is that the number of drug calls in the next time period are the same as those in the current period. With the exception of CCF and the random walk all models were estimated using the Stata statistical software package.
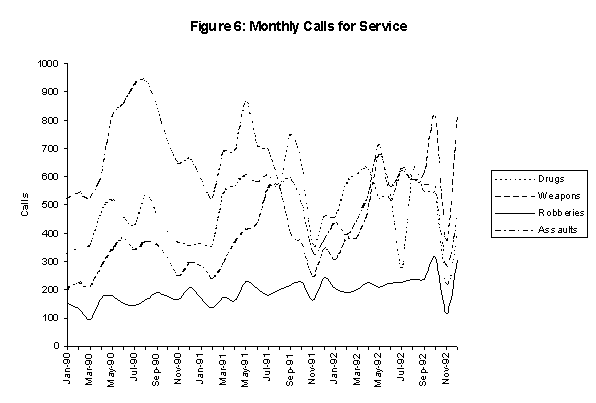
The CCF model was estimated using a learning rate of 0.001 and nine hidden units. Again these figures were arrived at via experimentation on the data. Other learning rates and a different number of hidden units may be optimal for different data sets. The connection weights were randomly initialized to values in the range [-0.1, +0.1].
Both the regression and chaotic cellular forecasting models were estimated using the first two years' worth of data. The last year was used as a holdout sample to test the robustness of the estimated parameters. Tables 5.2 through 5.7 report the results of the simple (OLS) regression, Poisson regression and Tobit regression estimates of model (5.7) and (5.8) on the training data set for one-step-ahead forecasts.
|
Table 5.2 Estimates on Training Data Set (No Spatially Lagged Averages) - Simple Regression |
|||||||||
|
Source |
Sum of Squared Errors |
Degrees of Freedom |
Mean Squared Error |
||||||
|
Model |
162212 |
7 |
23173.26 |
||||||
|
Residual |
45890 |
10672 |
4.30 |
||||||
|
Total |
208103 |
10679 |
19.49 |
||||||
|
Adj. R2 |
0.7793 |
F-Value |
7541.32*** |
Root MSE |
2.074 |
# of Obs. |
10680 |
||
|
Variable |
Coefficient |
Standard Error |
t-Value |
||||||
|
Constant |
0.0070305 |
0.0580121 |
0.121 |
||||||
|
Drugs |
0.8224579 |
0.0057901 |
142.045*** |
||||||
|
Weapons |
0.1488242 |
0.128355 |
11.595*** |
||||||
|
Robberies |
0.0125878 |
0.0211918 |
0.594 |
||||||
|
Assaults |
0.062614 |
0.0085916 |
7.288*** |
||||||
|
% Residential |
0.0099798 |
0.0586685 |
0.170 |
||||||
|
% Commercial |
0.4258341 |
0.1881995 |
2.263** |
||||||
|
Season |
-0.0853638 |
0.0738103 |
-1.127 |
||||||
|
Significance Levels: * = 0.1, ** = 0.05, *** = 0.01 |
|||||||||
The adjusted R-squared for the simple regression model without spatial lags was 0.7793. The F-statistic, significant at the 0.01 level, was 7541.32. However, only half of the estimated coefficients were statistically significant. Somewhat surprisingly the coefficient for the seasonality index was negative. Given that the number of drug calls for service tends to increase during the summer months one would have expected a positive coefficient. Not surprisingly, the number of drug calls for service in the previous time period had the largest coefficient, followed by the % of properties that are zoned commercial.
|
Table 5.3 Estimates on Training Data Set (No Spatially Lagged Averages) - Poisson Regression |
|||||
|
Goodness-of-Fit Chi2 |
Log Likelihood |
Pseudo R2 |
Model Chi2 |
||
|
20145.380*** |
-15697.372 |
0.4649**** |
27276.032*** |
||
|
Variable |
Coefficient |
Standard Error |
z-Score |
||
|
Constant |
-1.128023 |
0.0377612 |
-29.873*** |
||
|
Drugs |
0.0395313 |
0.0005303 |
74.551*** |
||
|
Weapons |
0.1004241 |
0.0017777 |
56.492*** |
||
|
Robberies |
0.0437552 |
0.0040948 |
10.686*** |
||
|
Assaults |
0.0643317 |
0.0015185 |
42.365*** |
||
|
% Residential |
0.9181392 |
0.0404966 |
22.672*** |
||
|
% Commercial |
1.054886 |
0.0757209 |
13.931*** |
||
|
Season |
-0.2396972 |
0.0334107 |
-7.174*** |
||
|
Significance Levels: * = 0.1, ** = 0.05, *** = 0.01, ****as reported by Stata |
|||||
Table 5.3 shows the results of the Poisson regression using model (5.7). The pseudo R-squared reported by Stata is 0.4649, which is significant at the 0.01 level. Unlike the OLS results, all of the coefficients are significant. The % of properties that are commercial and residential have the largest coefficients.
|
Table 5.4 Estimates on Training Data Set (No Spatially Lagged Averages) - Tobit Regression |
|||||
|
Log Likelihood |
Pseudo R2 |
Model Chi2 |
|||
|
-8909.5345 |
0.2564**** |
6142.94*** |
|||
|
Variable |
Coefficient |
Standard Error |
t-Value |
||
|
Constant |
-8.3880 |
0.2810 |
-29.847*** |
||
|
Drugs |
0.8700 |
0.0137 |
63.402*** |
||
|
Weapons |
0.4748 |
0.0318 |
14.912*** |
||
|
Robberies |
0.1067 |
0.0536 |
1.990** |
||
|
Assaults |
0.3587 |
0.0222 |
16.188*** |
||
|
% Residential |
2.8595 |
0.2617 |
10.927*** |
||
|
% Commercial |
4.8561 |
0.5767 |
8.420*** |
||
|
Season |
-0.2321 |
0.2510 |
-0.902 |
||
|
Significance Levels: * = 0.1, ** = 0.05, *** = 0.01, ****as reported by Stata Note: 8406 left censored observations at < 0.1, 2274 uncensored observations |
|||||
The Tobit regression results of model (5.7) shown in Table 5.4 indicate a pseudo R-squared of 0.2654, which is significant at the 0.01 level. Again, the most dominant coefficients are those of the ecological variables. 8406 observations were left censored.
|
Table 5.5 Estimates on Training Data Set (Spatially Lagged Averages) - Simple Regression |
|||||||||
|
Source |
Sum of Squared Errors |
Degrees of Freedom |
Mean Squared Error |
||||||
|
Model |
162378 |
13 |
12490.63 |
||||||
|
Residual |
45725 |
10666 |
4.29 |
||||||
|
Total |
208103 |
10679 |
19.49 |
||||||
|
Adj. R2 |
0.7800 |
F-Value |
2913.61*** |
Root MSE |
2.0705 |
# of Obs. |
10680 |
||
|
Variable |
Coefficient |
Standard Error |
t-Value |
||||||
|
Constant |
0.0323524 |
0.0712593 |
0.454 |
||||||
|
Drugs |
0.816167 |
0.0059132 |
138.025*** |
||||||
|
Weapons |
0.1283622 |
0.0135344 |
9.484*** |
||||||
|
Robberies |
0.0120371 |
0.0214847 |
0.560 |
||||||
|
Assaults |
0.0498935 |
0.0091128 |
5.475*** |
||||||
|
% Residential |
-0.007064 |
0.0736159 |
-0.096 |
||||||
|
% Commercial |
0.678445 |
0.2186717 |
3.103*** |
||||||
|
Season |
-0.1403245 |
0.0750493 |
-1.870* |
||||||
|
Drugs (Spat. Ave.) |
0.0112826 |
0.0164524 |
0.686 |
||||||
|
Weapons (Spat. Ave.) |
0.0619071 |
0.0317452 |
1.950** |
||||||
|
Robberies (Spat. Ave.) |
0.0316789 |
0.0571666 |
0.554 |
||||||
|
Assaults (Spat. Ave.) |
0.0487492 |
0.0206204 |
2.364** |
||||||
|
% Residential (Spat. Ave.) |
-0.0766389 |
0.1161294 |
-0.660 |
||||||
|
% Comm. (Spat. Ave.) |
-1.367454 |
0.485068 |
-2.819*** |
||||||
|
Significance Levels: * = 0.1, ** = 0.05, *** = 0.01 |
|||||||||
Table 5.5 reports the (OLS) results of model 5.8. The adjusted R-squared is 0.7800, which is statistically significant at the 0.01 level. Only approximately half of the coefficients were statistically significant, as in model (5.7). Interestingly, the coefficient of the spatially lagged average of the proportion of commercial properties had a strong negative influence.
|
Table 5.6 Estimates on Training Data Set (No Spatially Lagged Averages) - Poisson Regression |
|||||
|
Goodness-of-Fit Chi2 |
Log Likelihood |
Pseudo R2 |
Model Chi2 |
||
|
17386.336*** |
-14317.850 |
0.5119**** |
30035.076*** |
||
|
Variable |
Coefficient |
Standard Error |
z-Score |
||
|
Constant |
-1.89738 |
0.0528566 |
-35.897*** |
||
|
Drugs |
0.0333808 |
0.0006144 |
54.329*** |
||
|
Weapons |
0.0761946 |
0.0022289 |
34.185*** |
||
|
Robberies |
0.0146796 |
0.0048114 |
3.051*** |
||
|
Assaults |
0.043634 |
0.0018067 |
24.151*** |
||
|
% Residential |
0.5973702 |
0.049468 |
12.076*** |
||
|
% Commercial |
0.8313732 |
0.0845584 |
9.832*** |
||
|
Season |
-0.3538514 |
0.0364302 |
-9.713*** |
||
|
Drugs (Spat. Ave.) |
0.0775448 |
0.0035547 |
21.815*** |
||
|
Weapons (Spat. Ave.) |
-0.0106852 |
0.0066702 |
-1.602* |
||
|
Robberies (Spat. Ave.) |
0.2112664 |
0.0163722 |
12.904*** |
||
|
Assaults (Spat. Ave.) |
0.0474487 |
0.0056467 |
8.403*** |
||
|
% Residential (Spat. Ave.) |
1.113307 |
0.0699516 |
15.915*** |
||
|
% Comm. (Spat. Ave.) |
0.7582296 |
0.1932213 |
3.924*** |
||
|
Significance Levels: * = 0.1, ** = 0.05, *** = 0.01, ****as reported by Stata |
|||||
Table 5.6 reports the Poisson regression results on model (5.8). The pseudo R-squared, as reported by Stata, is 0.5119, which is statistically significant at the 0.01 level. As with model (5.7), all coefficients are statistically significant, and the ecological variables have the strongest influence.
|
Table 5.7 Estimates on Training Data Set (No Spatially Lagged Averages) - Tobit Regression |
|||||
|
Log Likelihood |
Pseudo R2 |
Model Chi2 |
|||
|
-8741.0613 |
0.2704**** |
6479.89*** |
|||
|
Variable |
Coefficient |
Standard Error |
t-Value |
||
|
Constant |
-9.3351 |
0.3455 |
-27.018*** |
||
|
Drugs |
0.8230 |
0.0139 |
57.171*** |
||
|
Weapons |
0.3501 |
0.0332 |
10.542*** |
||
|
Robberies |
0.0438 |
0.0537 |
0.816 |
||
|
Assaults |
0.2572 |
0.0231 |
11.156*** |
||
|
% Residential |
2.0991 |
0.3133 |
6.700*** |
||
|
% Commercial |
4.4018 |
0.7038 |
6.254*** |
||
|
Season |
-0.7324 |
0.2660 |
-2.754*** |
||
|
Drugs (Spat. Ave.) |
0.1426 |
0.0422 |
3.375*** |
||
|
Weapons (Spat. Ave.) |
0.2461 |
0.0848 |
2.903*** |
||
|
Robberies (Spat. Ave.) |
0.2972 |
0.1624 |
1.831* |
||
|
Assaults (Spat. Ave.) |
0.3609 |
0.0577 |
6.260*** |
||
|
% Residential (Spat. Ave.) |
1.5087 |
0.4468 |
3.376*** |
||
|
% Comm. (Spat. Ave.) |
-0.8892 |
1.6004 |
-0.556 |
||
|
Significance Levels: * = 0.1, ** = 0.05, *** = 0.01, ****as reported by Stata Note: 8406 left censored observations at < 0.1, 2274 uncensored observations |
|||||
The Tobit regression results of model (5.8) reported in Table 5.7 indicate a pseudo R-squared of 0.2704, which is significant at the 0.01 level. Again, the ecological variables appear to have the strongest influence, as do the number of drug calls for service in the previous time period for the current observation (not spatially lagged). With two exceptions all coefficients are statistically significant. As in model (5.7), 8406 observations were left censored at 0.1.
|
Table 5.8. Results of CCF Estimated Forecasts Compared to Regression Estimated Forecasts |
|||
|
Models Without Spatially Lagged Averages |
|||
|
Model |
Training Data Set |
Holdout Sample |
Iterations |
|
Simple Regression |
|||
|
R2 |
0.7795 |
0.7644 |
- |
|
SSE |
45890 |
22455 |
|
|
Mean % Error |
-128.16 |
-149.37 |
|
|
Poisson Regression |
|||
|
R2 |
0.4079 |
0.4302 |
- |
|
SSE |
197447 |
88787 |
|
|
Mean % Error |
633.99 |
516.91 |
|
|
Tobit Regression |
|||
|
R2 |
0.7108 |
0.6894 |
- |
|
SSE |
425369 |
198034 |
|
|
Mean % Error |
4784.72 |
4664.81 |
|
|
Models With Spatially Lagged Averages |
|||
|
Simple Regression |
|||
|
R2 |
0.7802 |
0.7644 |
- |
|
SSE |
45725 |
22449 |
|
|
Mean % Error |
-120.74 |
-149.23 |
|
|
Poisson Regression |
|||
|
R2 |
0.3383 |
0.3666 |
- |
|
SSE |
199444 |
89861 |
|
|
Mean % Error |
702.73 |
703.03 |
|
|
Tobit Regression |
|||
|
R2 |
0.6894 |
0.1887 |
- |
|
SSE |
457224 |
320908 |
|
|
Mean % Error |
4998.77 |
2904.63 |
|
|
Random Walk |
|||
|
Random Walk |
|||
|
R2 |
0.7725 |
0.7620 |
- |
|
SSE |
49988 |
24165 |
|
|
Mean % Error |
-93.30 |
-118.06 |
|
|
CCF |
|||
|
CCF |
|||
|
R2 |
0.8188 |
0.7800 |
4500 |
|
SSE |
37740 |
20926 |
|
|
* Note: The R-squared reported for CCF, Tobit, and Poisson, as well as the fit of the holdout sample using the regression coefficients is a simple squared correlation coefficient only, and can thus not be directly compared to the adjusted R-squared of the regression results on the training data set or the pseudo R-squared reported by Stata. |
|||
Table 5.8 compares the results of CCF to the other models, including the random walk. The results show that, overall only CCF and OLS could beat the random walk on both the training data set and the holdout sample. CCF still overfits somewhat, however, as evidenced by the drop in the fit of the holdout sample compared to the training data set, although the decline is still within the range of acceptability. Overall CCF reduces the sum of squared errors by about 17% on the training data set and by about 7% on the holdout sample compared to the closest competitor (OLS). CCF took only 4500 iterations to converge, which is a considerable improvement over early efforts (Olligschlaeger, 1997). The improvement in fit over the closest competitor is evidence that CCF was able to pick up nonlinearities in the data.
|
Table 5.9 Comparison of Models by Zero and Non-Zero Cells - Sum of Squared Errors |
||||
|
Models Without Spatially Lagged Averages |
||||
|
Model |
Training Data Set Zero Cells (MPE) |
Holdout Sample Zero Cells (MPE) |
Training Data Set Non-Zero Cells (MPE) |
Holdout Sample Non-Zero Cells (MPE) |
|
Simple Regression |
2199 (-163.59) |
1762 (-149.37) |
43691 (2.79) |
20693 (-5.56) |
|
Poisson Regression |
4786 (633.99) |
2248 (642.19) |
192691 (101.77) |
86540 (99.01) |
|
Tobit Regression |
325666 (6009.70) |
147515 (5992.37) |
99703 (256.50) |
50519 (236.48) |
|
Random Walk |
2000 (-120.64) |
1577 (-155.34) |
47987 (12.45) |
22588 (6.31) |
|
Models With Spatially Lagged Averages |
||||
|
Simple Regression |
2364 (-153.56) |
1874 (-191.30) |
43361 (0.60) |
20575 (-8.89) |
|
Poisson Regression |
9210 (865.43) |
4297 (884.56) |
190233 (101.31) |
85564 (97.51) |
|
Tobit Regression |
363951 (6286.25) |
169038 (3802.81) |
93274 (239.53) |
151060 (-92.59) |
|
CCF |
||||
|
CCF |
1179 (-150.87) |
1463 (-205.59) |
36560 (10.64) |
19463 (6.86) |
Table 5.9 further breaks down the comparison between those cells that are zero, i.e., had no drug related calls for service during a month's period, and those that had a least one call for service. This was done because crime data aggregated by areal units tend to have a Poisson distribution: most values are zero, and hot spots form a "spike" at the tail end of the distribution. When forecasting crime data by areal unit it is desirable to accurately capture the hot spots, rather than just correctly estimate that most areal units have in fact zero drug calls for service. With respect to multiple regression this would imply regression to the mean of zero with the tail end of the distribution being treated as outliers. For day to day police operations, however, it is important that police administrators have some means of predicting which areas are going to "flare" up.
It is clear both from the training data set results and the holdout sample reported in Table 5.9 that CCF consistently outperforms all of the other models. Indeed, CCF was the only model that was able to beat the random walk model in all categories. The only other model that came close to doing so were the OLS regression models. The uniformity of the results suggests that CCF is more accurately able to estimate the true functional form of the model. Most likely this is because it is able to incorporate nonlinearities in the data.
|
Table 5.10 Comparison of Models for Cells Where the Number of Drug Calls for Service is Zero at Time T and Non-Zero at Time T+1 - Sum of Squared Errors (Mean Percent Error in Parentheses) |
||
|
Models Without Spatially Lagged Averages |
||
|
Model |
Training Data Set |
Holdout Sample |
|
a - Simple Regression |
1846 (72.36) |
1071 (71.29) |
|
b - Poisson Regression |
3145 (123.94) |
1734 (121.38) |
|
c - Tobit Regression |
32309 (521.27) |
16113 (503.77) |
|
d - Random Walk |
2336 (91.37) |
1313 (91.60) |
|
Models With Spatially Lagged Averages |
||
|
e - Simple Regression |
1767 (69.69) |
1038 (67.65) |
|
f - Poisson Regression |
3206 (125.92) |
1850 (124.32) |
|
g - Tobit Regression |
30203 (498.77) |
23072 (71.11) |
|
CCF |
||
|
CCF |
1411 (65.04 - a,b,c,d,e,f,g) |
1005 (67.49 - b,c,d,f,g) |
|
Note: letters in parentheses indicate a statistically significant difference at the 0.01 level using a Wilcoxon signed rank test |
||
Table 5.10 compares the relative performance of the models for those grid cells that displayed zero drug activity at time t and greater than zero drug activity in the next time period. In effect Table 5.10 gauges the performance of the models on emerging drug markets, or their usefulness as an early warning system for previously unknown drug hot spots. Again, CCF outperforms the other models, although the margin of improvement over OLS is not as great as that of the previous tables. However, with the exception of the two OLS models on the holdout sample, the decrease in the sum of squared errors is statistically significant at the 0.01 level using a Wilcoxon signed rank test.
.
This paper has introduced a new spatio-temporal forecasting method - chaotic cellular forecasting - that is derived from cellular automata (a class of chaotic systems) and artificial neural networks. One implementation of CCF, a hybrid model of spatially varying input to hidden units weights and constant hidden to output unit weights and direct input to output unit connections was tested using GIS based data. Specifically, CCF was used to produce one-step-ahead forecasts of drug calls for service based on crime and ecological variables. The results were then compared to six other forecasting models as well as a random walk model and tested for robustness on a holdout data sample. The performance of CCF is quite promising. It outperformed all of the other models, albeit with varying degrees of success, and was the only model to consistently outperform the random walk model in all categories examined. One disadvantage of CCF is that, like all neural networks, there are currently no tests of statistical significance for the estimated weight structures. However, since in forecasting the main goal is to provide accurate and robust forecasts rather than to analyze relationships between dependent and independent variables this should not be an issue.
Although these early results of chaotic cellular forecasting are very encouraging, much work remains to be done. Within the realm of artificial neural networks the algorithm is a fairly simple one. There have been many recent advances in the type of networks used by CCF.
Future work will include incorporating some of the advances in artificial neural network technology mentioned above. For example, there are many ways in which backpropagation networks can be modified so that they converge more quickly to a solution. An additional improvement would be to employ genetic algorithms to develop self-optimizing network architectures. Also, this paper only used a single hidden layer. The literature suggests that for very complex input to output mappings, such as is possibly the case for spatio-temporal data, two or more layers may be more appropriate in that they increase the capability of the network to capture nonlinearities in the relationship between input and outputs units.
Rigorous testing with Monte Carlo data would also provide more insight, as would testing on larger data sets. Currently using larger data sets and more complex architectures is difficult given the speeds of computers. As outlined earlier, however, this should become a possibility in the very near future given the recent advances in computer speeds.
This dissertation has sought to make a number of contributions to the criminology, geography and forecasting literature by taking advantage of recent advances in computer technology and artificial intelligence and applying them to spatial analyses of crime. In particular, police departments around the country are making increasing use of advanced information systems such as GIS. This in turn provides researchers with high quality data and allows for the introduction of new modeling techniques which previously have not been applied in this area.
DMAP, discussed in chapter 2, is one example of an advanced computerized information system in use by police in the City of Pittsburgh. Although primarily intended as an investigative and administrative tool for police officers focusing on illicit street level drug dealing, DMAP also functions as a data gathering tool for other types of crime. In addition, DMAP integrates non-crime relate data such as property ownership information. Indeed, this dissertation would not have been possible without the data set collected by DMAP.
Chapter 3 in particular takes advantage of the fact that DMAP includes high quality location data on ecological variables such as land use and the built environment. This allowed the use of multiple regression techniques to study the effects of both traditional and ecological variables on illicit drug markets. The finding was that when ecological variables are included, the influence of traditional variables declines in importance.
Chapter 4 introduced a new spatial modeling technique: weighted spatial adaptive filtering (WSAF). The technique estimates spatially varying parameters of cross-sectional multivariate models, and includes a weighting scheme to discriminate between relevant and inappropriate sources of feedback from neighboring observations. WSAF was employed in an empirical study which provides evidence that spatial interaction, local context and spatially varying model parameters are important indicators of street level drug dealing.
Chapter 5 introduced a new spatial forecasting methodology which combines chaos theory and a version of artificial neural network, feedforward networks with backpropagation. The resulting technique, called chaotic cellular forecasting (CCF), was then used to forecast drug calls for service over a three year period in the City of Pittsburgh. The study used grid cell aggregated data derived from DMAP. The results of CCF were then compared to seven traditional forecasting models. It was found that CCF was significantly able to improve upon the forecasts of the other methods.
The two new modeling technologies introduced in this dissertation were only a first experimental design. Much work remains to be done. CCF in particular needs to be more thoroughly tested using Monte Carlo data as well as other data sets. Perhaps one of the most important aspects that requires attention is the classification of different types of changes in patterns that can occur over time and space. Different methodologies may be appropriate in different circumstances. Thus, it would be useful to determine which methodology, or, in the case of CCF, which neural network architecture works best in which situation.
Given that more and more police departments are switching over to new technologies, including integrated GIS, a pilot project testing CCF in a real life situation would be very useful. Many promising new technologies which perform very well in a lab environment fail when they are applied in practice. Indeed, this was the case with Perceptrons. For example, training of the CCF network using live data would be different from the way in which it occurred in chapter 5. Instead of using two years worth of data and then testing the robustness of the model on a holdout sample, the network would be retrained each time new data comes in. It is conceivable that over time the performance of the network would increase, as more and more data points are used in training. It would also be interesting to analyze how well CCF can adapt to changing patterns over time. In other words, if the functional form of spatial variation changes over time, can CCF adjust its weights accordingly and still perform well?
On the other end of the spectrum, there also a need for more basic research into how computerized mapping can aid law enforcement efforts. This includes not only research into the kinds of applications that police officers need, but also the various sources of information required and how they can be integrated. To date most commercial applications of GIS in law enforcement do not go beyond simple pin mapping, and only very few integrate other computerized information systems. Indeed, most GIS applications are standalone systems that require data transfers or downloads in order to produce maps.
Anselin, Luc (1988). Spatial Econometrics: Methods and Models, Dordrecht, Netherlands: Kluwer.
Bates, J. M., and Granger, C. W. J. (1969). "The Combination of Forecasts." Operations Research Quarterly, 20, 451-68.
Belsley, D., Kuh, E., and Welsch, R. (1980). Regression Diagnostics, New York: Wiley.
Blumstein, A., Cohen, J., and Farrington, D. P. (1987). "Characterizing Criminal Careers." Science, 238, 985-991.
Blumstein, A., Cohen, J., and Farrington, D. P. (1988). "Criminal Career Research: Its Value for Criminology." Criminology, 26: 1-35.
Box, G. E. P. and Jenkins, G. M. (1970). Time Series Analysis, Forecasting and Control, San Francisco: Holden-Day.
Brantingham, P. J. and Brantingham, P. L. (1984). Patterns in Crime. Macmillan.
Bretschneider, S. L. and Gorr, W. L. (1983). "Ad Hoc Model Building Using Time Varying Parameter Models." Decision Sciences 14, 221-39.
Brown, R. G. (1962). Smoothing, Forecasting, and Prediction of Discrete Time Series, Englewood Cliffs, NJ: Prentice-Hall
Carbone, R. and Longini, R. (1977). "A Feedback Approach for Automated Real Estate Assessment." Atmospheric Environment, 12: 241-48
Casetti, E. (1972). "Generating Models by the Expansion Method: Applications to Geographic Research." Geographical Analysis 4: 81-91
Casetti, E. (1973). "Testing for Spatial-Temporal Trends: An Application of Urban Population Density Trends Using the Expansion Method." Canadian Geographer 17: 127-36.
Cassetti, E. (1982). "Drift Analysis of Regression Parameters: An Application to the Investigation of Fertility Development Relations." Modeling and Simulation 13, 961-66.
Casetti, E. (1986). "The Dual Expansion Method: An Application to Evaluating the Effects of Population Growth on Development." IEEE Transactions on Systems, Man and Cybernetics SMC-16, 29-39.
Casetti, E. and Fan, C. (1991). "The Spatial Spread of the AIDS Epidemic in Ohio: Empirical Analyses Using the Expansion Method." Environmental Planning A 23: 1-23.
Cassetti, Emilio and Jones, J.P. eds. (1992). Applications of the Expansion Method. London: Routledge.
Clemen, R. T. (1989). "Combining Forecasts: An Annotated Bibliography." International Journal of Forecasting, 5, 559-83.
Cleveland, W. S. (1979). "Robust Local Weighted Regression and Smoothing Scatterplots." Journal of the American Statistical Association 74: 829-36.
Cleveland, W. S. and Devlin, S. J. (1988). "Locally Weighted Regression: An Approach to Regression Analysis by Local Fitting". Journal of the American Statistical Association 83, 596-610.
Cliff, A.D., Haggett, P., Ord, J.K., Bassett, K. and Davies, R. (1975). Elements of Spatial Structure. Cambridge, England: Cambridge University Press.
Cohen, L.E. and Felson, M. (1979). "Social Change and Crime Rate Trends: A Routine Activity Approach." American Sociological Review 44: 588-607.
David, M. (1977). Geostatistical Ore Reserve Estimation, Amsterdam: Elsevier.
Dunn, C. S. (1980). "Crime Area Research." In Crime: A Spatial Perspective, edited by D. E. Georges-Abeyie and K. D. Harries. New York: Columbia University Press.
Felson, M. (1987). "Routine Activities and Crime Prevention in the Developing Metropolis." Criminology 25:911-31.
Foster, S. A. and Gorr, W. L. (1986). "An Adaptive Filter for Estimating Spatially Varying Parameters: Application to Modeling Police Hours Spent in Response to Calls for Service." Management Science, 32: 878-89.
Foster, S. A. W., Gorr, W. L. and Wimberly, F. C. (1992). "Comparison of Functional and Drift Analysis Approaches to Expansion Modeling: Evaluation of Federal Policies on the Supply of Physicians." In Casetti, E. and Jones, J. P. III (eds.): Applications of the Expansion Method. London: Routledge.
Getis, A. (1994). "Spatial Filtering in a Regression Framework: Experiments on Regional Inequality, Government Expenditures and Urban Crime." In Anselin, L. and Florax, R. (eds.): New Directions in Spatial Econometrics. Amsterdam: North Holland.
Gardner, M. (1970). "The Fantastic Combinations of John Conway's New Solitaire Game 'Life'". Scientific American, 223:4, pp. 120-23.
Gorr, W.L. and Olligschlaeger, A.M. (1994). "Weighted Spatial Adaptive Filtering: Monte Carlo Studies and Application to Illicit Drug Market Modeling." Geographical Analysis, 26: 67-87.
Granger, C. W. J. (1969). "Investigating Causal Relations in Econometric Models and Cross-Spectral Models." Econometrica, 37: 424-438.
Haining, T. (1990). Spatial Data Analysis in the Social and Environmental Sciences, Cambridge, England: Cambridge University Press.
Hornik, K., Stinchcombe, M. and White, H. (1989). "Multilayer Feedforward Networks are Universal Approximators." In: Neural Networks, Vol. 2, Pergamon Press.
Kabel, J. R. (1992). "A Geographic Perspective on AIDS in the United States: Past, Present and Future." Ph.D. Dissertation, Geography Department, The Pennsylvania State University, State College, PA.
Kroese, B. J. and Van der Smagt, P. P. (1993). An Introduction to Neural Networks, lecture notes, University of Amsterdam, Netherlands.
Lander, B. (1954). Toward an Understanding of Juvenile Delinquency. Columbia University Press.
Lapedes, A. and Farber, R. (1987). Nonlinear Signal Processing Using Neural Networks: Prediction and System Modeling. Technical Report LA-UR-87-2662, Theoretical Division, Los Alamos National Laboratory, Los Alamos, NM.
Makridakis, S. and Wheelwright, S. C. (1977). "Adaptive Filtering: An Integrated Autoregressive/Moving Average Filter for Time Series Forecasting." Operations Research Quarterly, 28: 425-37.
Maltz, M. D. (1993). "Crime Mapping and the Drug Market Analysis Program (DMAP)." In Workshop on Crime Analysis Through Computer Mapping Proceedings: 1993, edited by C. R. Block and M. Dabdoub, Illinois Criminal Justice Authority.
McEwen, J.T. and Taxman, F. S. (1994). "Applications of Computerized Mapping to Police Operations." In Crime, Place and Police, edited by J. E. Eck and D. Weisburd, Crime Prevention Series, Vol. 4.
Minsky, M. and Papert, S. (1969). Perceptrons. Cambridge, PA: MIT Press.
Newbold, P. and Granger, C. W. J. (1974). "Experience with Forecasting Univariate Time Series and the Combination of Forecasts." Journal of the Royal Statistical Society 137: 131-46.
Olligschlaeger, A. M. (1997). "Artificial Neural Networks and Crime Mapping." In McEwen, T. and Weisburd, D. (eds.): Computerized Crime Mapping, Crime Prevention Series, Rutgers University Press.
Pickover, C. A. (1990). Computers, Pattern, Chaos and Beauty. New York: St. Martin's Press.
Poli, I. And Jones, R. D. (1994). "A Neural Net Model for Prediction." Journal of the American Statistical Association, 89:117-21.
Robbins, H. and Monro, S. (1951). "A Stochastic Approximation Method." Annals of Mathematical Statistics, 22: 400-407
Roncek, D. W. and Baier, P. A. (1991). "Bars, Blocks and Crimes Revisited: Linking the Theory of Routine Activities to the Empiricism of 'Hot Spots'." Criminology 29: 725-53.
Rossmo, K. (1995). "Place, Space and Police Investigations: Hunting Serial Violent Criminals." In Eck, J. and Weisburd, D. (eds.) Crime and Place. Monsey, NY: Criminal Justice Press.
Rumelhart, D. E. and McClelland, J. L. (1988). Parallel Distributed Processing, Vols. 1 and 2, Cambridge, MA: MIT Press
Rumelhart, D. E., Hinton, G. E. and Williams, R. J. (1988). "Learning Internal Representations by Error Propagation." In Rumelhart, D. E. and McClelland, J. L. (eds.) Parallel Distributed Processing, Vol. 1, Cambridge, MA: MIT Press
Schmid, C. F. (1960). "Urban Crime Areas: Part II." American Sociological Review 25: 655-78.
Schroeder, M. (1991). Fractals, Chaos and Power Laws. New York, New York: W.H. Freeman.
Sharda, R. and Patil, R. B. (1990). "Neural Networks as Forecasting Experts: An Empirical Test." In: IEEE INNS Joint Conference on Neural Networks, II, 491-494, Washington, DC: January, 1990.
Shaw, C. R. (1929). Delinquency Areas. University of Chicago Press.
Sherman, L. W., Gartin, P. R. and Buerger, M. E. (1989). "Hot Spots of Predatory Crime: Routine Activities and the Criminology of Place." Criminology 27: 27-55.
Skogan, W. (1986). "Fear of Crime and Neighborhood Change." In A. J. Reiss and M. Tonry, Communities and Crime 8, University of Chicago Press.
Spring, J. W. and Block, C. R. (1988). "Finding Crime Hot Spots: Experiments in the Identification of High Crime Areas. " Paper presented at the 1988 annual meeting of the Midwest Sociological Society, Minneapolis, MN
Tang, Z., Almeida, C. and Fishwick, P. A. (1990). Time Series Forecasting Using Neural Networks Vs. Box-Jenkins Methodology. UF-CIS Technical Report TR-90-3, Computer and Information Sciences Department, University of Florida, Gainesville, FL.
Tobler, W. R. (1969). "Geographical Filters and their Inverses." Geographical Analysis, 1, 234-53.
Tobler, W. R. (1979). "Cellular Geography." In Gale, S. and Olsson, G. (eds.): Philosophy of Geography. Dordrecht: Reidel.
Toffoli, T. and Margolus, N. (1987). Cellular Automata Machines: A New Environment for Modeling. MIT Press Series in Scientific Computations, Cambridge: MIT Press.
Trigg, D. W. and Leach, D. H. (1967). "Exponential Smoothing with an Adaptive Response Rate." Operational Research Quarterly 18: 53-59.
Weiss, S. M. and Kulikowski, C. A. (1991). Computer Systems That Learn. Morgan Kaufmann, San Mateo.
White, H. (1988). "Economic Prediction Using Neural Networks: The Case of IBM Daily Stock Returns." Proceedings of the IEEE International Conference on Neural Networks, San Diego
Widrow, G. and Hoff, M. E. (1960). "Adaptive Switching Circuits." Institute of Radio Engineers, Western Electronics Show and Convention
1. Geocoded Data Files Accessed Directly By DMAP
|
BARS.DAT |
||
|
Purpose: Data file for the bars point coverage. |
||
|
Variable |
Size/Type* |
Description |
|
type |
2c |
type of Liquor License |
|
license |
6i |
number of liquor license |
|
title |
45c |
title of bar (if any) |
|
name |
45c |
name of owner |
|
number |
5i |
street number |
|
fdpre |
2c |
street direction |
|
fname |
35c |
street name |
|
ftype |
4c |
street type |
|
city |
15c |
city |
|
state |
2c |
state |
|
zip |
5c |
zip code |
|
nuisance |
1c |
nuisance bar flag |
|
address |
38c |
parsed address field |
|
*c denotes a character field, i an integer field and b a binary field |
||
|
CALLS.DAT |
||
|
Purpose: Main file for call for service data. |
||
|
Variable |
Size/Type* |
Description |
|
addver |
1c |
address version |
|
street_number |
4b |
house number |
|
street_name |
60c |
street name |
|
city |
3c |
city code |
|
intersection |
20c |
closest intersection street |
|
disposition |
3c |
disposition of call for service |
|
date |
4b |
data of call for service |
|
time |
4b |
time of call for service |
|
event_number |
4b |
internal event number |
|
ccr |
4b |
ccr number |
|
nature_code |
6c |
nature code |
|
zone_num |
2c |
police zone number |
|
event_number_e |
4b |
related EMS event number |
|
event_number_f |
4b |
related fire event number |
|
event_number_o |
4b |
related other event number |
|
event_number_p |
4b |
related police event number |
|
census_block |
4c |
1980 census block number |
|
census_tract |
6c |
1980 census tract number |
|
initiate |
2c |
internal flag |
|
address |
38c |
parsed address field |
|
*c denotes a character field, i an integer field and b a binary field |
||
|
LOCATION.DAT |
||
|
Purpose: Main file for PSMS incident data. |
||
|
Variable |
Size/Type* |
Description |
|
loctocase |
4b |
internal PSMS case number linking a location to an incident |
|
dateocc |
4b |
date of incident |
|
timeocc |
4b |
time of incident |
|
number |
4b |
street number |
|
fdpre |
2c |
street prefix |
|
fname |
40c |
street name |
|
fdsuf |
4c |
street type |
|
inctype |
1c |
type of incident |
|
offrep |
1c |
flag for offense report |
|
loctores |
4b |
internal PSMS number linking an arrest report to the residence of the arrestee |
|
drugs |
1c |
drug incident flag |
|
vice |
1c |
vice incident flag |
|
rob |
1c |
robbery incident flag |
|
bur |
1c |
burglary incident flag |
|
auto |
1c |
auto theft incident flag |
|
ewap |
1c |
weapons incident flag |
|
hom |
1c |
homicide incident flag |
|
ass |
1c |
assault incident flag |
|
sex |
1c |
sex crimes flag |
|
oth |
1c |
other incident type flag |
|
sro |
1c |
stolen/recovered flag for auto thefts |
|
address |
38c |
parsed address field |
|
*c denotes a character field, i an integer field and b a binary field |
||
|
PROP.DAT |
||
|
Purpose: Property file data. |
||
|
Variable |
Size/Type* |
Description |
|
ward |
2c |
ward |
|
tract |
2c |
tract |
|
space-1 |
1c |
dummy space |
|
map-zero |
1c |
map flag |
|
map |
3i |
map number |
|
block |
1c |
map block |
|
parcel |
3i |
parcel number |
|
parcel-suf |
1c |
parcel suffix |
|
parcel_suf-3 |
3c |
additional parcel suffix |
|
street-number |
8c |
street number |
|
street-half |
1c |
half number flag |
|
street-name |
18c |
street name |
|
street-suffix |
2c |
street suffix |
|
etal-rear-code |
1c |
code for rear entrance |
|
name-1 |
24c |
first owners name |
|
name-2 |
24c |
second owners name |
|
name-3 |
24c |
third owners name |
|
owner-add |
24c |
owner address |
|
owner-city |
24c |
owner cirt |
|
data-block |
10c |
mainframe internal number |
|
cen-block60 |
3c |
1960 census block |
|
cen-tract60 |
2c |
1960 census tract |
|
cen-blk70 |
3c |
1970 census block |
|
cen-tract70 |
2c |
1970 census tract |
|
tax-land-assess |
9i |
land tax assessment |
|
tax-bldg-assess |
9i |
building tax assessment |
|
tax-area |
9i |
area tax assessment |
|
land-use-curr |
4c |
current land use |
|
corp-code |
4c |
corporation type code |
|
zoning |
3c |
zoning restrictions |
|
slope |
1c |
slope of land |
|
prob-code |
3c |
unknown |
|
assess-type |
1c |
type of assessment |
|
parcel-class |
1c |
classification of parcel |
|
exempt-corp-code |
1c |
code for tax exempt corporation |
|
exempt-land-ass |
9i |
tax exempt land assessment |
|
exempt-bldg-ass |
9i |
tax exempt building assessment |
|
exempt-area-ass |
9i |
tax exempt area assessment |
|
last-sale-month |
2i |
month of last sale |
|
last-sale-year |
2i |
year of last sale |
|
last-sale-price |
8i |
price last sold for |
|
last-sale-type |
1c |
type of last sale |
|
space-2 |
1c |
dummy space |
|
address |
38c |
parsed address |
|
*c denotes a character field, i an integer field and b a binary field |
||
|
PROPADD.DAT |
||
|
Purpose: Data file for the address coverage against which other data is geocoded. |
||
|
Variable |
Size/Type* |
Description |
|
lotadd |
9c |
lot-block number |
|
number |
6i |
street number |
|
fdpre |
2c |
street direction |
|
fname |
18c |
street name |
|
fdsuf |
4c |
street type |
|
address |
38c |
parsed address |
|
*c denotes a character field, i an integer field and b a binary field |
||
|
RESIDES.DAT |
||
|
Purpose: Data file containing the residences of people associated with PSMS incidents. |
||
|
Variable |
Size/Type* |
Description |
|
rfu1 |
4b |
internal PSMS relate number |
|
rfu2 |
4b |
internal PSMS relate number |
|
phone |
13c |
phone number |
|
date |
4b |
last known data at this address |
|
city |
12c |
city |
|
state |
2c |
state |
|
apt |
5c |
apartment number |
|
building |
5c |
building number |
|
street |
50c |
street address |
|
county |
10c |
county of residence |
|
zip |
9c |
zip code |
|
address |
38c |
parsed address |
|
*c denotes a character field, i an integer field and b a binary field |
||
2. PSMS Data Files Indirectly Accessed by DMAP
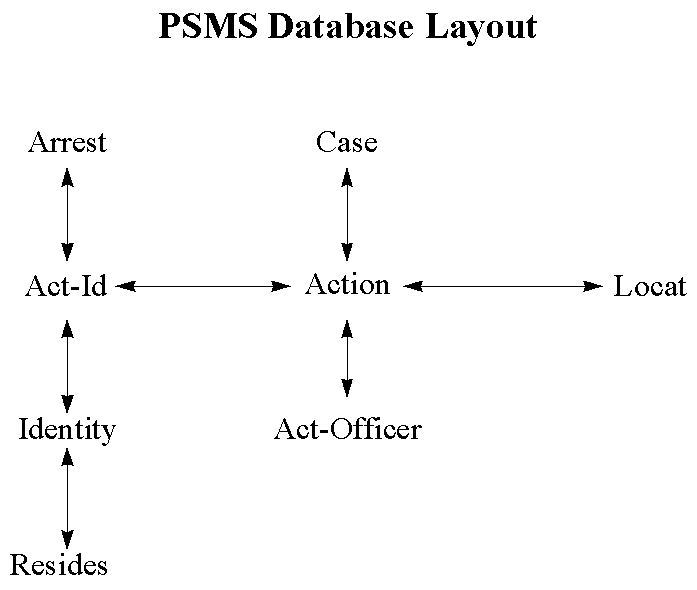
|
ACT_OFFICER |
||
|
Purpose: Contains file pointers to the names and ranks of officers that are associated with a particular action (report). |
||
|
Variable |
Size/Type* |
Description |
|
rfu1 |
4b |
internal relate number |
|
rfu2 |
4b |
internal relate number |
|
id |
4b |
id number of officer |
|
type |
4c |
personnel type |
|
detail |
4c |
detail assigned |
|
badge |
4c |
badge number |
|
division |
4c |
division assigned to |
|
*c denotes a character field, i an integer field and b a binary field |
||
|
ACTION |
||
|
Purpose: Each case record has one or more related action records. An action record is generated each time a report is filed. |
||
|
Variable |
Size/Type* |
Description |
|
rfu1 |
4b |
internal relate number |
|
rfu2 |
4b |
internal relate number |
|
rfu3 |
4b |
internal relate number |
|
rfu4 |
4b |
internal relate number |
|
off_code |
13c |
offense code |
|
writedate |
4b |
date report was written |
|
writetime |
4b |
time report was written |
|
type |
4c |
type of report |
|
orig |
1c |
original or supplemental report flag |
|
ucr |
4c |
ucr reporting hierarchy status |
|
agency |
4c |
agency status |
|
lastdate |
4b |
date of last update |
|
lasttime |
4b |
time of last update |
|
*c denotes a character field, i an integer field and b a binary field |
||
|
ARREST |
||
|
Purpose: Contains all charges associated with arrest reports. |
||
|
Variable |
Size/Type* |
Description |
|
rfu1 |
4b |
internal relate number |
|
rfu2 |
4b |
internal relate number |
|
prob |
1c |
flag for on probation |
|
walkin |
1c |
flag for walk-in arrest |
|
charge |
9c |
charge filed |
|
court |
10c |
hearing court |
|
otn |
10c |
offender tracking number |
|
disdate |
4b |
disposition date |
|
heardate |
4b |
date of hearing |
|
heartime |
4b |
time of hearing |
|
*c denotes a character field, i an integer field and b a binary field |
||
|
CASE |
||
|
Purpose: Main point of entry in the PSMS file system. Each incident has one associated case record. |
||
|
Variable |
Size/Type* |
Description |
|
rfu1 |
4b |
internal relate number |
|
dateocc |
4b |
date case opened |
|
timeocc |
4b |
time case opened |
|
dateend |
4b |
date case closed |
|
timeend |
4b |
time case closed |
|
agency |
4c |
agency involved |
|
ccr |
4b |
ccr number |
|
*c denotes a character field, i an integer field and b a binary field |
||
|
IDENTITY |
||
|
Purpose: Data file containing the identities of persons involved with PSMS incidents. |
||
|
Variable |
Size/Type* |
Description |
|
rfu1 |
4b |
internal relate number |
|
rfu2 |
4b |
internal relate number |
|
idtype |
1c |
type of identity record |
|
last |
18c |
last name |
|
first |
12c |
first name |
|
middle |
12c |
middle name |
|
suffix |
c3 |
name suffix |
|
race |
1c |
race |
|
sex |
1c |
gender |
|
dob |
4b |
date of birth |
|
sysnum |
4b |
internal person id number |
|
lastdate |
4b |
date of last update |
|
lasttime |
4b |
time of last update |
|
citizen |
1c |
flag for US citizen |
|
realid |
1c |
flag for alias/real name |
|
employment |
20c |
place of employment |
|
occupation |
20c |
occupation |
|
busaddress |
50c |
business address |
|
buszip |
9c |
business zip code |
|
busphone |
c13 |
business phone |
|
*c denotes a character field, i an integer field and b a binary field |
||
|
LOCAT |
||
|
Purpose: Original PSMS location data. |
||
|
Variable |
Size/Type* |
Description |
|
rfu1 |
4b |
internal relate number |
|
street |
4b |
street number (linked to a code table) |
|
number |
4b |
house number |
|
type |
1c |
street type |
|
cross |
4b |
cross street name (linked to code table) |
|
place |
4b |
place name (linked to code table) |
|
*c denotes a character field, i an integer field and b a binary field |
||
|
RESIDES |
||
|
Purpose: Date file containing the residences of persons involved in PSMS incidents. |
||
|
Variable |
Size/Type* |
Description |
|
rfu1 |
4b |
internal relate number |
|
rfu2 |
4b |
internal relate number |
|
phone |
13c |
phone number |
|
date |
4b |
date of last connection |
|
city |
12c |
city of residence |
|
state |
2c |
state |
|
apt |
5c |
apartment number |
|
building |
5c |
building number |
|
street |
50c |
street address |
|
county |
c10 |
county |
|
zip |
c9 |
zip code |
|
*c denotes a character field, i an integer field and b a binary field |
||