School of Computer Science

Carnegie Mellon University

Pittsburgh, PA 15213

When a student is presented with an algebra word problem such as P0 in Table 1 and asked to provide a symbolic expression (rather than a numerical answer) he is doing what we call symbolizing. For instance, the symbolic expression for P0 is "800-40*m". In studying symbolization skills we have focused on algebra story problems but our results may be relevant more generally to symbolization skills needed in using a calculator, programming a spreadsheet, or computer programming. As these computational devices take over more of the symbol manipulation of algebra, symbolization is becoming an increasingly central skill. As part of an effort to build computerized instructional support for symbolizing, we are trying to understand how students learn to symbolize and test that understanding by developing a cognitive model.

Much of the prior work on word problem solving has focused on students' comprehension abilities. Paige & Simon(1979) proposed a model that included a direct translation component. Paige & Simon took Bobrow's(1968) computer program STUDENT, that did symbolization of certain classes of algebra story problems, as a foundation for their cognitive model. They compared symbolization to translation from English to French, which they said involved taking each French word, looking it up in a French to English dictionary, and writing down the answers with some possible changes to inflections, and rearrangements due to syntax rules. Paige & Simon's model included a limited use of schemata for problems like "age" problems. These schemata, when recognized as appropriate for a problem, brought to bear certain assumptions about what to expect as well as certain world knowledge that is usually not stated in algebra story problems (e.g., that we all age at the same rate and ages are positive integers). Mayer (1981) extended the study of schemata and classified a large number of story problems into 90 different schemata and suggested we might want to teach children to recognize schemata. Mayer suggested that students first identify the general class of problem and then bring to bear schemata that pull out of the situation some of the numbers to fill expected slots. Other research on arithmetic story problem solving has focused on the role of comprehension (Cummins et. al., 1988, LeBlanc & Weber-Russell, 1996, Lewis & Mayer, 1987, and Stern, 1993). Cummins et. al. "suggest that much of the difficulty children experience with word problems can be attributed to difficulty in comprehending abstract or ambiguous language." The general conclusion from much of the above research is that comprehension rules and schema detection skills are key knowledge components students must acquire to become competent problem solvers.

More recently Koedinger & Anderson (in press) found evidence that acquiring such comprehension skills is not sufficient for symbolization competence. They found that on 36% [((result-unknown=55%) - (symbolize=35%))/55%] of problems that students comprehended well enough to find a numerical answer, they nevertheless failed to correctly symbolize. This result suggests that in addition to comprehension difficulties, students have difficulty in "symbolic production." That students have substantial difficulties on the symbolic side of the translation process is further supported by Koedinger & Tabachneck's (1995) results that show, contrary to many algebra teachers' predictions, that students are better at solving certain algebra word problems than they are at solving the mathematically equivalent problems given in algebra symbols. These two results together suggest that a large amount of the difficulty of symbolization can be explained by a "foreign language hypothesis". If you ask a student to translate an English sentence into Greek and observe that the student fails, it is not necessarily that they lack the comprehension skills of English but maybe that they lack the production skills for Greek. Similarly, students may fail in story problem solving not because they lack English comprehension skills, but rather because they cannot "speak algebra".

To compensate for this lack of algebra language fluency, students fall back on arithmetic knowledge. Figure 1 shows a student who appears to have correctly described the mathematical sequence needed to solve for a value if given "h" but who fails to express that knowledge in the correct algebraic form. Instead of writing 500/(h-2) the student has indicated that first she would subtract 2 from "h" which would result in a new unknown that she again calls "h". Then she indicated that 500 should be divided by this new number. She uses the non-algebraic notation for division that is taught in elementary school. This example illustrates very well that a student can have an understanding of the quantitative structure of a problem but not be able to symbolize because they lack the correct knowledge for producing algebraic sentences.

Figure 2 is another example that demonstrates comprehension and quantitative understanding but not the ability to correctly generate the algebraic symbols. Her answer is similar to the answer in Figure 1 in that they both indicate the process that should be used to solve for an answer, but fail to output that answer in standard algebraic form. The use of the equals sign in this example appears to grow out of the way students use the equal sign as "gives" in elementary arithmetic in which it is not uncommon to see students chain together steps with equal sign like 3*4=12-5=7 (Sfard, et. al., 1993). Since 72-m can not be simplified the student uses a new variable "n" to stand for the result and then continues.

Our goal is to better understand what these symbol production skills are and how students might better learn them. What capabilities do more competent students have that poorer students do not? What kinds of scaffolds might we provide to assist student learning? To address these questions, we performed a difficulties factors assessment whereby we sampled student performance on a set of 128 problems created by systematically modifying 8 core problem situations along 4 binary factor dimensions. These 4 factors represent specific hypotheses about what causes students symbolization difficulties and how scaffolds might ease the symbolization process.

Again consider the problem P0 from Table 1. This is a hard problem for ninth grade beginning algebra students, with only 13% of the students in the experiment (described below) answered it correctly. What makes this problem hard? Maybe what makes this problem hard is 1) having to compose the symbolic translation of parts of the problem into a complete translation of the whole problem, 2) the presence of the distractor phrase "2400 yards wide", 3) comprehending the text well enough to translate the phases into operators and numbers and knowing which numbers are matched up with which operators, or 4) the presence of an algebraic variable "m" as opposed to the numeric constants students are already familiar with from arithmetic instruction. In the following sections we provide motivation for the consideration of each of these factors and illustrate them as they modify problem P0 (see Table 1).

Singley, Anderson & Givens (1991) reported that some students fail to solve multi-step story problems even when they can solve the individual parts that make them up. We desire to know whether or not this is simply the expected effect of having to do multiple steps each of which results in an accumulated chance of failure. Alternatively, the multi-step problem may be even harder (or easier) than the combined probability of the correct performance of the individual steps separately. Consider P1, which is the two sub-problems of PO, which we call the decomposed version of P0. Of course we would expect that solving a single part of this problem is easier than solving P0. The more interesting question is "Is solving P0 easier than solving both parts of P1?" Maybe if comprehension of the text is a limiting factor then the more wordy P1 will make it harder.

As Paige & Simon observed, less competent symbolizers appear to sometimes rely exclusively on direct translation and do not evoke any semantic processes to recognize, for instance, that a negative board length is impossible. We have observed (Tabahneck, Koedinger, & Nathan, 1994) that novice symbolizers exhibit other kinds of shallow processing. In particular, students will often produce "symbol soup" by guessing at the answer using the given numbers and symbols but getting position or operations wrong. To the extent that novice symbolizers employ such a guessing strategy (perhaps as a fall back when more specific knowledge is lacking), we should see more errors on problems that involve an extra distractor quantity (such as "2400 yards wide" in P2) than on problems that do not.

A second justification for including the distractor factor is that it provides a way to test an alternative hypothesis for why composed problems may be more difficult than decomposed problems. If less competent students are, in fact, sometimes guessing at answers using random sequences of quantities and operators in the problem, then composed problems should be more difficult than decomposed problems because the possible combinations of the quantities in the composed, no-distractor problems (these are the total number of possible guesses) is greater than the sequences of the two quantities and operator in the separate parts of the decomposed no-distractor problem. This hypothesis suggests that decomposed distractor problems should be more difficult than composed no-distractor problems.

Given the attention past research has given to the role of comprehension in the symbolization process, our third factor tests a possible scaffolding technique that attempts to help students comprehend the problems more effectively. This technique is to give the student a hint that reexpresses the problem in a form that is more amenable to direct translation to symbols. These hints are in a form that would clearly facilitate performance of a computer model like the STUDENT program Paige & Simon used. Consider the comprehension hints given in P3. Notice that the hints identify what mathematical operator is to be used, while the original problem statement did not. Also note that the form of the hint is in the simple form of <Subject_Quantity> "is equal to" <Quantity1> <Operator> <Quantity2>, where <Subject_Quantity>,<Quantity1> and <Quantity2> are replaced with a verbal description of a quantity noun phrase, and <operator> is replaced by either "plus", "minus", "multiplied by" or "divided by." This simple form makes it possible for a left to right scan of the problem to work efficiently. Also note that these verbal recodings identify what number or variable is matched with each quantity. Since these hints identify the operation to be used, they eliminate the need for schemata or world knowledge such as having to know the distance-rate-time formula.

As mentioned earlier, Koedinger & Anderson(in press) found that for certain classes of problems students are better able to find a numerical answer than write a symbolic expression for the same problems. Koedinger & Anderson hypothesized that asking students to compute concrete instances (problems without a variable) of a general problem would facilitate symbolization of that problem. To test this hypothesis, they designed a scaffolding technique called inductive support and implemented it as part of an intelligent tutor.

We can illustrate the inductive support scaffolding technique with our running example P0. The scaffolding involved two questions that asked students to solve the problem if the variable were replaced with a constant, for instance, "How far is Ann from the dock in 4 minutes?". After answering these concrete arithmetic problems, students were asked to write the symbolic expression. Students in this inductive support tutor were shown to learn more than students using an alternative "textbook" tutor. The tutor's design was adapted based on this study so that the current tutor (Koedinger, Anderson, Hadley, Mark, 1995) has a "Pattern Finder" component where, rather than just answering these concrete questions, students are asked to show how to get answers for successive small values of x, namely, 2, 3, and 4. In the example above, students are expected to answer "800 - 40 * 2", then "800 - 40 * 3" and "800 - 40 * 4". Next, they are to induce the pattern to get the abstract expression "800 - 40 * x". It has come as somewhat of a surprise that making this last step it not at all difficult for students and that, in fact, it is only the first step, writing the expression when x is 2, that students have any difficulty with. We began to wonder whether this first step really is easier than the final goal of writing the abstract expression. If not, the Pattern Finder may not be such a good scaffolding technique. Thus, we added the presence of variable factor to this assessment to test whether writing a concrete expression (e.g., "800 - 40 * 11" as in P4) is in fact easier than writing an abstract expression (e.g., "800 - 40 * m "as in P1).

Given the four binary factors that were studied there were sixteen different possible combinations of the factors. These 16 different possible combinations were crossed with 8 different cover stories and distributed in a latin square design among 16 test forms that balanced for each factor. Given that students tend to perform worse on items near the end of a test, the order of various problems was systematically varied on each (e.g., the 8 composed, distractor, no hint, no variable problems were in the 8 different position on 8 different forms). However, because the cover story factor was not a variable of critical interest, the 8 cover stories appeared in the same order on each form (to do otherwise would have required many more forms). All eight cover stories had two operators implicit in the story so that the composed version required a two operator answer, while the decomposed version required two separate answers that each had one operator. The subjects were 79 ninth grade students in the first month of a low-level algebra course from an affluent suburb of Pittsburgh. Each student was randomly given one of the 16 different test forms and had 14 minutes to complete the test. After two class periods of instruction on such problems, students were again given a random form as a post test. Each test was then graded and no partial credit was given. A decomposed problem was considered correct only if both parts were answered correctly.

To test for effects of the four factors we performed both an item analysis and a subject analysis as recommended by Clark (1973). We performed an item analysis on students’ mean performance on the 128 different problems appearing on the pre- and post-test forms. Separate item means were computed for the pre- and post-tests. We performed a four factor (2*2*2*2) ANOVA on the item means.

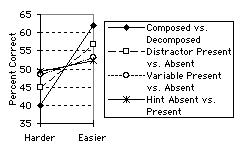
Figure 3 illustrates the relative impact of the four factors. The effect of the comprehension hints appears small at best (3.1% difference in favor of hint problems) and this difference is not statistically significant(F(1,238)=1.127, p<.2894). Similarly, the presence of a variable is also small at best (4.5% difference in favor of no variable problems) and not statistically significant (F(1,238)=1.531, p<.217). In contrast the distractor effect was considerably larger (11.8% difference in favor of no distractor problems) and statistically significant (F(1,238)=8.135, p<.0047). The composition factor had by far the largest effect (22% difference in favor of the decomposed problems), and was statistically significant (F(1,238)=37.048, p<.0001). No statistically significant interactions were found in the full ANOVA model.

To verify that these effects generalize across subjects as well as across items, we performed subject analysis as well. We performed four repeated measure ANOVAs with each factor as a within-subjects variable. Again there were statistically significant effects for distractor (F(1,66)=14.018, p=.0004) and composition (F(1,66)=52.059, p=.0001) but again no statistically significant effects of variables (F(1,66)=.739 p=.3932) or hints (F(1,66)=1.306, p=.2573).

Figure 3: Percent Correct for the Four Factors

These results show that a two operator problem is harder than both of the parts that make it up put together. We call this the composition effect. What skills are many students missing that prevent them from being able to deal with composed problems even though they are able to deal with the sub-problems individually? We describe two alternative models of the composition effect and the relative evidence in support of them.

Argument Generalization Model We hypothesize that the whole is harder than the sum of its parts because there is extra difficulty in putting the symbolic translations of the parts together to form a symbolic translation of the whole. We hypothesize that many students start their study of algebra with knowledge components (e.g., ACT-R production rules (Anderson 1993)) that enable them to symbolize only one operator problems because their production rules only allow for single numerals or variables (e.g., 40 or m) to be used as arguments to the mathematical operators, as opposed to whole subexpressions (e.g., 40*m or 800-x). Such students can answer 800-x but not 800-40*m because 40*m is a subexpression and they don't know how to substitute a subexpression into another expression. A student at this stage might fall back on his arithmetic rules and produce an answer like that shown in Figure 2 which appears to indicate an inability to compose subexpressions. Such a student would probably be the sort Koedinger & Anderson had identified as being able to solve for numerical answers but unable to symbolize correctly. As students tackle multi-operator problems they must generalize these rules to allow for symbolized subexpressions to be used as arguments to other operators enabling them to write 800-40*m. We find support for this explanation in Sfard & Linchevski (1993) who argue that students gradually progress through a stage where their conception of an expression changes from viewing an expression as a recipe to viewing an expression as a first class object. It might be that as a student makes this transition in their understanding of an expression they also can generalize their productions to perform subexpression substitution.

Combinatorial Search(CS) Model A second hypothesis is that the composition effect can be explained purely in terms of a combinatorial search model, in which a composed problem is harder because of the exponentially increasing number of possible sequences of arguments and operators. The large effect of distractors leads us to conclude that many students engage in some form of guessing, particularly as a fallback strategy when having difficulty. The difficulty of guessing grows with the complexity of problems, particularly as the number of possible combinations of given quantities and inferred operators grows. The composed, no distractor problems have three quantities to choose from whereas there are only two quantities to choose from in each of the two parts of the decomposed, no distractor problems. Thus, it may be that the composition effect is the result of this added complexity, and not the result of a missing or over specialized skill as hypothesized in the Argument Generalization model.

We tried a number of ways of estimating complexity depending on different assumptions. However, all of them predicted, contrary to the data, that the distractor effect should be bigger than the composition effect. We present one such estimation which has the following assumptions about how a student may guess at an answer: 1) students can pick out what numbers or variables are present in the problem and which operators will be used, 2) students know the general syntactic form of a symbolic sentence, particularly that operators need to be written between quantities, and 3) students will not use the same argument (variable or number) twice. To simplify the calculation, we ignore the difficulty of knowing when to add parentheses and assume that the operators in the problem are non-commutative so the student has to get the order of the arguments correct. Essentially, this comes down to assuming that to guess correctly, students must pick the correct order for the arguments and operators. We compare the probability of doing so for various problem types.

Let us first calculate the probability of getting the correct order for a composed problem, starting with the leftmost argument and moving right. The probability of getting the first argument correct is 1/3 since there are three possible numbers to put first. Similarly, the student picks one of the two inferred operators for the first operator slot (1/2). Then given our assumption of a non-replacement strategy, the probability of choosing the next argument correct is 1/2 since there are two remaining arguments. The final operator and arguments are then determined. So the combined probability of getting the correct answer is (1/3)(1/2)(1/2)(1/1)(1/1)=1/12.

Now we calculate the probability of guessing the correct answer for a decomposed non-distractor problem. Since there are only two arguments present, the probability of selecting the first argument is 1/2. The operator and the second argument are then both determined. So to get one part of a decomposed non-distractor problem correct is 1/2 and to get both parts correct is (1/2)(1/2)=1/4. Since 1/12 is less than 1/4 we see that this model does predict that there will be a composition effect. But the model does not predict the relative effect of distractors as we will now show.

Finally, consider a decomposed distractor problem. The probability of selecting the first argument is 1/3, since there are now 3 arguments present in the problem statement. The operator is determined, but the last operator is 1/2, which yields a total for one part of (1/3)(1/2)=1/6 and a total for the two parts together of (1/6)(1/6)=1/36.

In summary the SC model predicts that the distractor effect(1/36) will be larger than the composition effect (1/12). However, the data shows that the composition effect is larger (22%) than the distractor effect (11%). The composition effect was found to be statistically different from the distractor effect when we compared the means for composed, non-distractor problems with decomposed, distractor problems (F(1, 238) = 5.2, p < .05).

We now consider an explanation for the surprising absence of a statistically significant effect of the comprehension hints. After all, these hints recoded the story problem into a simpler form that is more amenable to direct translation. The hints also identified what the operators should be, which quantities to use with those operators and which order to put the operators in. These results are consistent with the view that the comprehension of these sentences is not that large a stumbling block, particularly when compared with the stumbling block of learning to deal with composed problems. But despite the fact that hints were not statistically significant there is evidence that the hints did help for the decomposed problems. The trend in favor of the hint problems was much larger (a 7% difference) on the decomposed problems than on the composed problems ( .01% difference). We hypothesize that the students who benefited from the hints were less able students and were the students most likely not to have the skills to deal with composed problems (as outlined in the Argument Generalization Model). We speculate that the hints might be more helpful if they directly addressed composition. A single "composed" hint for P3 could be:

Although prior work (Koedinger & Anderson, in press) has shown that solving a concrete problem for an unknown can be easier than doing abstract symbolization (e.g., writing "800 - 40 * x"), in this study we found that concrete symbolization (e.g., writing "800 - 40 * 2") is not much easier, if at all, than abstract symbolization (the small trend in favor of concrete symbolization was not statistically significant). As discussed above, this result has implications for the design of the "Pattern Finder" component of the PAT algebra tutor. The evidence from Koedinger & Anderson provided some support for the hypothesis that solving concrete problems aids students in symbolizing. The "Pattern Finder" is based on a further hypothesis that making this solution process more explicit through concrete symbolization would be an even better scaffold. The results of the current study put this hypothesis into question. At minimum, it suggests that the Pattern Finder should require students to answer the concrete problem before doing the concrete question (e.g., first, "How far is Ann from the dock in 2 minutes?" and then "Write down how you got that answer?"). Alternatively, since it appears that composing rather than abstracting is the real crux of the symbolization problem, we should focus our attention on developing a scaffolding technique that directly addresses composition.

One possible scaffolding technique for composition would be to tutor students to introduce variables for the subexpression and symbolize just the parts as the student in Figure 3 did spontaneously. Next, provide instruction on doing symbolic substitution. Another possible scaffolding technique would be to first ask students to symbolize any needed subexpressions, before attempting to symbolize the whole expression. For example, on P0, first ask students to symbolize "the distance Anne has rowed back towards the dock" and once they answer "40*11" ask them to use that subexpression to symbolize the final answer. The scaffold might also prompt students to indicate what quantity name represents the subexpression.

The large effect of the composition factor in this study, relative to the small or absent effect of comprehension hints, provides a strong case against the almost exclusive emphasis in previous research on language comprehension as the major stumbling block for students. A focus on language comprehension may be appropriate for the younger students learning arithmetic story problem solving. However, to address the difficulties of older students learning the new language of algebra, we need greater focus on the language production skills needed to "speak algebra".