When a student is presented with an algebra word problem such as problem CS in Table 1 and asked to provide a symbolic expression (rather than a numerical answer), she is doing what we refer to as symbolizing. For instance, the symbolic expression for CS is "(72-m)/4." In studying symbolization skills we have focused on algebra story problems but our results may also be relevant more generally to symbolization skills needed in using a calculator or programming a spreadsheet or computer. As these computational devices take over more of the symbol manipulation of algebra, symbolization deserves, and is receiving, increasing instructional emphasis. We are trying to understand how students learn to symbolize. To test that understanding we are building a cognitive developmental model which will be used in an intelligent tutoring system.

Much of the prior work (Cummins et. al., 1988; LeBlanc & Weber-Russell; 1996, Lewis & Mayer, 1987; Paige & Simon, 1979) on word problem solving has focused on students' comprehension abilities. Cummins et. al. "suggest that much of the difficulty children experience with word problems can be attributed to difficulty in comprehending abstract or ambiguous language." The general conclusion from the above research is that comprehension rules are key knowledge components students must acquire to become competent problem solvers.

This brings us to the first naturally intuitive hypothesis about what makes algebra symbolization difficult. What we call the generalization hypothesis flows naturally from the previous literature that has focused on comprehension difficulties caused by abstract language. An important conceptual leap for students is to move from the concrete grounded world of arithmetic problems to the more abstract world of algebra problems with variables. According to this hypothesis, what is hard about algebra is the generalization ability needed to think about a problem with an abstract variable, as opposed to a concrete known.

But more recent research by Koedinger & Anderson (in press) found evidence that acquiring such comprehension skills is not sufficient for symbolization competence. They reported that in 36% [((result-unknown=55%) - (symbolize=35%))/55%] of problems that students comprehended well enough to find a numerical answer, students nevertheless failed to correctly symbolize. We call the difference between the students’ performance on symbolization problems and on similar arithmetic problems the symbolization effect.

To determine if the symbolization effect is well-explained by the generalization hypothesis we (1997) performed an assessment in which we compared students’ performance on symbolization problems (like problem CS) with their performance on arithmetic symbolization problems. We could turn problem CA into an arithmetic symbolization problem simply by changing the final question to "Write an single expression that shows all the computations you would need to do in order to find how much she can spend on each sister." The correct answer for this problem would be "(72-32)/4." Arithmetic symbolization problems are a special type of symbolization problem that have no variables. We found no statistically significant difference between students performance on these two types of problems. This suggests that the presence of a variable did not increase difficulty, thus calling into question the usefulness of the generalization hypothesis’s focus on the variable per se as the factor that causes the symbolization effect.

An alternative hypothesis was suggested by another factor we tested. We found what we called the composition effect. The composition effect is the difference in student performance on what we call composed problems, like CS, and their decomposed analogs (DS1 and DS2), which are two separate problems from the student’s point of view, but for analysis purposes they are treated as a single problem and the problem is correct only if both parts are correct. The decomposed version of a composed problem is made by dividing the composed problem into two separate questions that each ask for one of the steps required to solve the composed version. Our results showed that there was a significant composition effect because many students could correctly answer both parts of a decomposed problem but fail to correctly answer the composed version. In other words, in this case, the whole is greater than the sum of its parts. The size of this composition effect overshadowed the small and not statistically significant difference, mentioned above, between arithmetic symbolization and symbolization.

We suspected that the cause of the symbolization effect was actually the composition effect. We will illustrate with an actual student who answers "72-m=n/4=" for CS. This student demonstrates that she knew the two steps she would need to perform if she had been given the arithmetic version CA. This student must learn how to correctly represent these two steps. She uses a placeholder variable, possibly because she does not know how to represent anything but a single operation at a time. For the expert it is obvious that "72-m" can be treated in the same way any number is treated. But the novice, who looks at "72-m" as a recipe and not as an object of reflection, does not know that she can operate on this quantity directly by adding parentheses and "/4". We call this missing skill articulating composition and we suspect that it is this difficulty that explains why symbolization problems are so much harder then arithmetic.

The two factors we studied were 1) arithmetic vs. symbolization (CA vs. CS and DS vs. DA) crossed with 2) composed vs. decomposed (CS vs. DS and CA vs. DA). Remember that the decomposed problem DS is actually one problems from the analysis point of view, but two separate problems from the student’s point of view. In our previous study (1997) we may have even underestimated the size of the composition effect, because we had a few students who would answer "(72-m)/4" for DA2. These students had noticed the superficial similarity of the two problems parts of a decomposed problem and interpreted the second one to be linked to the first. To avoid such misinterpretation by students we superficially changed a few aspects of the second part of the decomposed problems including the participants name. We also changed the numbers (making sure not to not decrease the difficulty of the arithmetic) to ensure that the results of the first part of a decomposed problem did not appear as a given in the second part of the problem. For example, DA2 was changed to "Rebecca made 81 dollars working at the grocery store. She decided to give her mom 25 dollars for Mother’s Day and put the remainder in her savings account. How much can she put in the savings account?" We found this strategy worked well and students did not think the two problems were connected.

The articulating composition hypothesis suggests that there should be no composition effect for arithmetic, but a large composition effect for symbolization. The reasoning behind this is that students know how to combine steps in an arithmetic problem, but they don’t know how to say, in symbols, how to put two steps together. Therefore, it predicts that there should be many students who know how to do both composed arithmetic problems and decomposed symbolization problems but fail to do composed symbolization problems. The two hypotheses differ in their predictions because the articulating composition hypothesis predicts an interaction between these two factors, while the generalization hypothesis does not predict an interaction and instead predicts one broad symbolization effect.

Given the two binary factors that were studied, there were four different problem types: composed symbolization, composed arithmetic, decomposed symbolization and decomposed arithmetic. These 4 problem types were crossed with 8 different cover stories and distributed in a Latin square design among 4 test forms that were balanced for each factor. Therefore each form had two problems of each type. Given that students tend to perform worse on items near the end of a test, the order of various problem types was systematically varied on each form. The cover-stories were not a variable of critical interest, and from our previous DFA we knew the performance on the cover stories would vary considerably. We used 6 of the 8 cover stories used previously and added two new cover stories to replace the two easiest cover stories from the prior study. Because we wanted to be able to compare the performance of students on cover stories we made two versions of each form that differed only in the order of the problems. The subjects were 76 ninth grade students in the first month of a regular-level algebra course from an urban high school in Pittsburgh. Two subjects were dropped for lack of participation in the test. Each student was randomly given one of the 8 different test forms and enough time to complete the test. Each test was then graded and no partial credit was given. A decomposed problem was considered correct only if both parts were answered correctly.

To test for the effect of the two factors we performed both an item analysis and a item analysis as recommend by Clark (1973). We performed a subject analysis on the students mean score for each of the four problem types. We performed a full two-factor (2*2) repeated measures ANOVA with each factor as a within-subject variable. We found significant effects of symbolization (F(1,73)=170.8, p<.0001) and of composition (F(1,73)=22.4, p<.0001.) but not the expected interaction (F(1,73)=1.024, p>.31). To verify that these effects generalize across items as well as across subjects, we performed an item analysis on students’ mean performance on the 32 different items (8 cover stories and 4 problem types) appearing on the test. We performed a full two-factor (2*2) ANOVA on the item means. Each factor was treated as a repeated measure. We found significant effects of symbolization (F(1,28)=55.476, p<.0001) and a smaller effect of composition (F(1,28)=13.26, p<.0083). The size of the symbolization effect was much larger then the size of the composition effect. Contrary to the prediction of the articulating composition hypothesis, there was not a significant interaction (F(1,28)=.821, p>.395), and this will be addressed below. Since the subject and the item analysis agree, we can be confident that both effects are real and generalize across the larger populations of both similar students and similar items.

We were initially surprised at the absence of the expected interaction, but upon investigation we saw that the individual variation, as shown by the histogram in Figure 1, was very large. Figure 1 shows how average student performance changes as their ability level increases. The lower-performing students, with total scores of 1, 2 and 3, are all at the floor for symbolization. They also show a composition effect during arithmetic problems. This is the exact opposite interaction we were expecting to see, but its cause is intuitively sensible. Students first learn to deal with the easier arithmetic problems, and the lower-performing students will show competence only in these. The fact that there is a composition effect among the arithmetic problems will be explored below. The middle-performing group (total scores of 4) show that the composition effect for arithmetic problems is going away as overall performance improves. The high-performing students ,with total scores of 5, 6 and 7, are doing equally well on both types of arithmetic problems and are improving on symbolization but primarily decomposed symbolization. In other words, the students show the interaction that the articulating composition hypothesis predicted.

To statistically characterize the individual variation we witnessed, we classified the subject population into a top-performing half and a bottom-performing half (using total score). We performed a full three-factor (2*2*2) ANOVA on the average of students’ means, again treating our two difficulty factors as within-subject repeated measures, and treating the factor of "top half vs. bottom half" as a between subjects factor. Again we had highly significant effects of symbolization (F(1,280)=172.5, p<.0001) and composition (F(1,280)=22.1, p<.0001). None of the three possible two-way interactions were close to statistical significance (P>.24 in all cases), but we did find a highly significant (F(1,280)=14.0, p<.0004) three-way interaction. Again, to verify that these effects occurred across items as well as across subjects, we did a three-factor (2*2*2) ANOVA on the item means, treating all three factors as within item repeated measure factors. Again, the only significant effects were the two main effects for symbolization (F(1,56)=50.1, p<.0002) and composition (F(1,56)=11.7, p<.012) and the three-way interaction (F(1,56)=9.4, p<.0183).

We will speculate below as to whether or not the composition effects seen in arithmetic(at the low end) and in symbolization (at the high end) are caused by a single effect or two separate effects. Our articulating composition hypothesis suggests that they are different effects and this will be explored now. We will then explore the other transitions we observed, which were not the main focus of the experiment, but nevertheless provide us with insight into the composite skills for composed symbolization.

Our articulating composition hypothesis predicted that there would be an additional cognitive hurdle for students to be able to solve composed symbolization problems. When we look at the top-performing half of the students we see the interaction which suggests that composed symbolization problems are unduly difficult. But how is that we get this average performance? Are most of these students demonstrating the same effects? The answer is "some, but not all." Let us call the prerequisites to being able to do a composed symbolization problem the ability to do both decomposed symbolization and composed arithmetic problems. Then 40% of the students who have met the prerequisites for composed symbolization, failed to solved a composed symbolization problem. When we say a student has met the prerequisites, we mean that a student was able to do at least one composed arithmetic problem, as well as one decomposed symbolization problem. there were 43 students who met this criterion, and 17 of them failed to solve a composed symbolization problem. We think that these 17 students are missing the knowledge of how to compose two symbolic expression together.

These 17 students made a total of 34 errors on composed symbolization problems and we would like to see if these errors are consistent with the articulating composition hypothesis. The largest category of errors are the 8 examples of errors where students wrote only the first step (i.e. one student wrote "72-m" for problem CS.) These errors are consistent with the articulating composition hypothesis, because a student that doesn’t know how to put two steps together might simply stop once she gets to a point where she doesn’t know how to continue. There were 3 errors of missing parentheses and one student who incorrectly used parentheses. These errors are also consistent with what one would expect from a person who can both symbolize single steps and do the arithmetic for two step word problems, but doesn’t yet know how to put two symbolizations together. It is also good to see that the missing-parentheses errors are responsible for a small portion of this effect. Many of the other errors are not easily categorizable and don’t give us much insight into what the student was thinking. It is true that about a third of the errors of students who appeared to be trying to overcome this hurdle are those that the articulating composition hypothesis would predict.

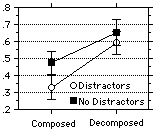
Our articulating composition hypothesis is what Newell(1990) would have called a knowledge-level explanation as opposed to a symbol-level explanation. We hypothesize that students are missing a certain bit of knowledge (e. g., production rules) that we can point to. But an alternative explanation of the additional difficulty of composed symbolization problems could be made at the symbol level. For example, maybe both symbolization problems and composed problems put a burden on working memory, and when these two factors combine, there is a strong interaction. We looked for evidence of such a symbol-level explanation by seeing if the composition effect while doing symbolization problems increased under a working memory load. Conveniently we have data to make this comparison, from our previous difficulty factors assessment. In this we studied both composition while symbolizing as well as the effect of distractor numbers. To illustrate, we had studied problem DS1 with and without a distractor phrase where we changed the problem to read "6 cars" rather then just "cars." We found a large effect for these distractor phrases, and we claim that this may be due to an increased working memory load. If the composition effect in symbolization problems is a working memory phenomenon we should expect to see the composition effect increase for distractor problems. Unfortunately, the results are inconclusive. Figure 2 shows a trend towards the predicted interaction but it is not significant (F(1,250)=1.48, p=.23).

But we do have evidence that conclusively shows that a knowledge-level component is definitely present. In our previous work (1997) we conjectured that if the hard part is composing steps together, then instruction focused on teaching students just the missing knowledge should improve their performance, even if divorced from practice on word problems. We haven’t space for a full reporting, but in short, we trained 39 students on problems like "Let X= 72-m. Let B= X/4. Write a new expression for B that composes these two steps." We then looked for transfer from the learning of this skill to students’ improvement on algebra symbolizing. In a single hour of training on this skill, we saw statistically significant increases in student performance on algebra symbolization as a result of training on symbolic substitution, even factoring out gains due to using parentheses correctly. This is possibly the strongest evidence we could present in favor of the articulating composition hypothesis. This result also supports the more general idea that there is greater difficulty on the production side rather then the comprehension side of translation, since these students improved without practice reading algebra word problems; the only practice they had was composing expressions together.

We now consider one of the transitions students must make before being able to deal with composed symbolization problems. This transition occurs when students learn decomposed symbolization problems. The evidence suggests that this transition is difficult. Fully one-third of the students who demonstrated competence (at least one correct) in the decomposed arithmetic problems could not do get any of the decomposed symbolization problems correct (let alone the composed one). This is a substantial effect that results in an additional 108 errors occurring (152 errors on decomposed symbolization problems while only 44 errors on decomposed arithmetic problems). What is the explanation for this symbolization gap of 108 errors? We note that there were many more "no answers" increasing from 12 to 57, but these "no answer" responses do not give us much insight into what is causing the difficulty. We now look at four different explanations that might account for why there are so many more errors.

The first hypothesis to explain the symbolization effect in decomposed problems is similar to the articulating composition hypothesis in that we focus on difficulties students have with production and not with comprehension. We will introduce two types of errors that are analogous to the sorts of errors made when learning a natural language. One such error is to say words in the wrong order, for instance, writing "m-72" when "72-m" is intended. We call these reversal errors. A second language production error is to use the wrong verb. For instance, writing "72+m" when "72-m" is intended. We call these wrong verb errors. But just because a person has written "72+m" does not mean we can assume they meant "72-m" so we will have to compare the error rates on symbolization problems with the number of analogous errors on arithmetic problems(for instance the number of people who added 72+32 to get 104 for problem DA2 in Table 1) It turns out that there are 7 errors of students using the wrong verb to arrive at a arithmetic answer. In contrast, for symbolization problems, there are 31 such errors. The increase in these wrong operator errors is due to the fact that that students’ difficulties arise not so much in English comprehension but in symbolic production. We see a similar pattern for the reversal errors, with no such errors occurring for arithmetic problems (nobody answers "-40" for DS2) while there are 12 such errors for symbolization problems. The difference in these simple articulation errors accounts for about 40% of the symbolization gap.

A second explanation is a possible consequence of the generalization hypothesis. Consider the 6th grade student who has never seen a variable before and is suddenly confronted with a problem with a variable for the first time. She would probably be totally confused and be inhibited from using that variable in her answer. She might be much more likely to randomly guessing using the more familiar numbers from the problem. Or she might answer as one student of ours did on several of the symbolization problems: "Not enough info". This leads to the prediction that novices are inhibited from using a variable. Of the students who gave an answer 38 answers did not contain the given variable even though in a decomposed problem there are only two numbers. This accounts for 35% of the symbolization gap. But there is a consistency problem with this variable inhibition hypothesis. In previous research we (1997) found that students’ ability to do arithmetic symbolization (e.g. answering with "72-32" rather then "40") was not significantly different (F(1,30)=.9, p>.35) from their ability to do algebraic symbolization (e.g. answer with "72-m"). However, we do note that the trend in the data was particularly large and in the predicted direction: the absolute performance on decomposed problems rises from 58% for arithmetic symbolization problems to 68% for symbolization problems with a variable. Furthermore, the students in the current study were generally at a lower level where variable inhibition may be greater. On the 6 cover-stories that the two populations had in common the percentage correct, on average, for symbolized problems was significantly different (F(1,10)=7.292, p<.02) with this present group averaging a low 27.2% while the previous group averaged a higher 42.8%.

A third hypothesis is that the symbolization effect for decomposed problems is caused by the fact that students may be using back-up strategies (like repeated addition: 40+40+40) for the arithmetic problems instead of the direct arithmetic strategy (e.g. 3*40) that is necessary for symbolization. We looked at all of the responses students gave to the arithmetic problems to see if we saw any evidence that students were using any math operations other than those expected, and found no evidence to support this hypothesis. At the same time, since students did not always show their work, we can not rule this out.

A fourth explanation for the presence of a symbolization effect in decomposed problems is what we call the semantic support hypothesis. If a student actually has numbers that they can use to compute answers they have the advantage of being able to look at the answer to detect violations with the semantics of the problem. We discussed above that there were no reversal errors on arithmetic problems but 12 on symbolization problem. Maybe the reason reversal errors don’t occur on decomposed problems is that if a student calculates "-40" she will quickly detect that a negative number of dollars to give to the sisters does not make sense. The semantic support hypothesis also suggests that even without doing any of the arithmetic, it might be easier for a student to figure out which operator to use if they know the relative size of the numbers given: students seem to have heuristics like "if one number is much larger then the other, then division is likely", in addition to heuristics like "always subtract the smaller number from the larger." So a student might benefit more by having numbers rather then variables even before she actually does any math. In our previous work, though we failed to find a significant difference (F(1,30)=.9, p>.35) between the performance on arithmetic symbolization vs. algebraic symbolization problems (as mentioned in the introduction), there was a difference of average percentage correct of about 10% from 58% correct to 68% correct. This suggests that there might be a role for the semantic support hypothesis that helps students use heuristics based on the size of numbers as well as heuristics that check the result of arithmetic computations for semantic violations. Neither of these strategies is possible if the problem has a variable present. Further research is needed to conclusively distinguish between the merits of these explanations.

The third developmental transition we detected was the gap shown by students who could not do composed arithmetic problems as well as decomposed arithmetic problem (which leads to what we call a composition effect in the decomposed problems). The gap is not large; there were 42 errors on decomposed problems while composed problems had 52. Again we notice that 10 of the answers for composed problems were the result of doing just the first of two required steps. These students possibly stop early because they are not reading the question carefully. There were only 5 students who were able to get a decomposed problem correct but failed to get any other type of problem including composed arithmetic problems correct. More generally, there were 24 students whose performance on composed arithmetic problems was worse than their performance on decomposed arithmetic problems. We would assume that this composition effect is partly explained by reference to cognitive models like LeBlanc and Russell (1996) that attempt to explain arithmetic word problem performance based on working memory load considerations. That is, composed problems are somewhat harder to read. It also might be that some students do not bother to re-read such problems even in the face of this high working memory load.

Based on these results of our difficulties factors assessment (here and in Heffernan & Koedinger, 1997), we have begun to create a developmental model of how students learn to symbolize. Contrary to common belief and the emphasis of prior cognitive science research, student’ difficulty in algebra word problem solving appears less related to comprehension difficulties and more related to difficulties in producing symbolic expressions, particularly expressions that involve more than one operator. We will summarize three main transitions this model. At the start of the developmental progression are students (two in this study) who fail to get any of the problems correct and we will ignore them. At the first non-trivial level, we saw five subjects who showed competence in decomposed arithmetic problems (where competence is at least one of the two problems correct) but failed to show competence in any other problem type. We speculated that their poorer performance on composed problems might be due to working memory limitations or related to difficulties comprehending more complicated composed stories. The students at this level show evidence predicted by the generalization hypothesis. In going to the next level students must learn to deal with composed arithmetic problems. They most likely need to improve their reading skills and make sure they answer the question asked. Twenty-four students had made this transition to competence in composed arithmetic but we not successful on any symbolization problems.

The next hurdle students surmount is learning how to deal with decomposed symbolization problems. It is interesting to note that no student was competent in decomposed symbolization problems who was not also competent in composed arithmetic. This is most likely due to the fact that students see composed arithmetic problems in elementary school, but most see variables much later. There were at the level of showing competence in both composed arithmetic and decomposed symbolization, but were not successful on any of the composed symbolization problems. We considered four alternative hypothesis regarding what students need to learn to make this transition to competence on simple decomposed symbolization problems.

At the highest level there were 25 students who were able to get one of the composed symbolization problems correct (only one student got both composed symbolization problems correct). In making this transition to competence in composed symbolization problems, students learn how to combine the articulation of individual steps.

We will limit ourselves to one instructional design suggestion that can be derived form this developmental model. In helping students transition from competence at symbolizing one operator problems to competence at symbolizing multiple operator problems, we recommend practice on symbolic substitution problems. At the face of it, such problems seem totally unrelated to translating word problems to symbols. However, our cognitive analysis and difficulty factors assessments have identified substantial overlap in the skills required for these apparently unrelated tasks. Furthermore, we have preliminary evidence that training on substitution transfers to symbolization.