1. Introduction
2. Problem Definition
3. Proposed Approach
• 3.1. Workload characterization
• 3.2. Model construction
• 3.3. Training workload generation
4. Publication list

System management cost is becoming the dominant factor in overall system cost nowadays. Autonomous systems, such as self-tuning database systems and self-managed storage systems, aim at reducing management cost by automating administration tasks. Besides the ability to identify performance bottlenecks, these systems can eliminate bottlenecks by re-allocating resources without human intervention. Performance prediction in such self-adaptive systems is extremely important because any decision on resource re-allocation requires multiple rounds of performance evaluations on a large number of configurations. Therefore, statistical performance models are essential because of their computational efficiency. These device models can be pre-built by the device manufacturers and shipped with devices themselves.

This thesis proposes to develop storage device models by learning device behavior through "training." This approach treats devices as black boxes, that is, neither the model itself nor the model construction algorithm is aware of the internals of the modeled storage device. Device behavior is described as a function of workloads, and in the training period, the model learns the behavior by observing the device under a set of training workloads. The advantage of this approach is that constructing a device model is fully automated and we can model any like-interfaced components. Furthermore, the device models take advantage of existing machine learning tools and are efficient and accurate.

The learining-based device modeling approach needs to address the following two issues. First, machine learning tools usually require the input data to be data points in a multi-dimensional Cartesian space. In order to transform workloads into such data points, we need efficient workload characteristic metrics. Previous work, however, usually involves parameters of empirical distributions, thus, is inappropriate. Second, a suite of high-quality training workloads is essential in order for the models to capture the device behavior under all possible workloads.

This thesis provides answers to both issues. The contributions of this thesis are:

• We propose an iterative process to construct black-box device models with machine learning techniques. The entire process is fully-automated and is general enough to model any type of storage devices. Furthermore, the framework is applicable to other system component modeling.
• We develop the entropy plot metric to quantify the spatio-temporal behavior of I/O workloads. This metric captures both the temporal burstiness and spatial locality in three scalars, making it ideal for the workload transformation. In addition, the entropy plot metric allows easy replication of the workload characteristics in synthetic workloads to facilitate other applications, such as system design evaluation.
• We explore two ways to construct device models based on machine learning tools and investigate a hybrid approach to combine the best of the two worlds.
• The framework uses a feedback machenism to build the training workloads iteratively. The training set, built by adaptive sampling techniques, is more efficient than uniform sampling.
• We demonstrate the power of the storage device models using a sample application, automatic data layout.

Our goal is to develop a model for a given storage device to predict a common workload's performance on the device. The device could be a single disk or a disk array. A workload is a sequence of disk requests. The workload performance is an aggregate performance measure, such as the average or 90th percentile response time. That is, the device model takes a sequence of disk requests as input and predicts the aggregate performance measure of the workload.

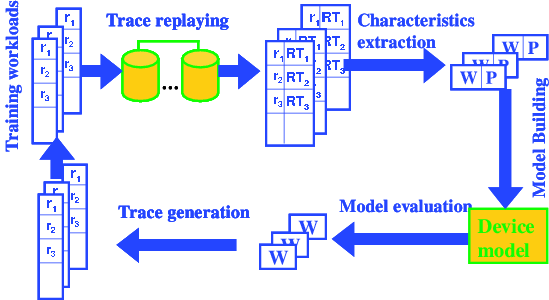
We propose an iterative process based on machine learning techniques to solve the device modeling problem. The approach, shown in Figure 1, assumes that the model construction algorithm can feed any workloads into the modeled device and observe its behavior for a certain period of time, also known as training. The algorithm then build a device model based on the observed response times. A feedback mechanism allows adaptive sampling and improves the model accuracy by incrementing the training set.

Figure 1: Constructing a device model through training.

The framework consists of three components. The workload characterization part extracts important characteristics of workloads and expresses them as vectors, also known as workload descriptions. The model construction part employs existing machine learning tools to build device models. The training workload generation part generates the training workloads iteratively.

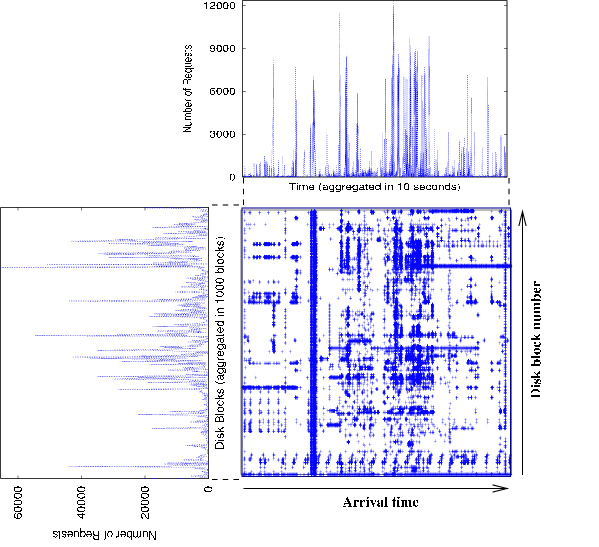
The goal of this step is to develop a metric that allows us to express important workload characteristics using a set of scalars, or workload descriptions, so that device models can distinguish workloads of different performance by these characteristics. The difficulty lies in the complex correlation structures of I/O workloads. On one hand, we observe burtiness along arrival time, and skewed popularity of disk blocks. On the other hand, there is a strong correlation between arrival time and location of disk requests. Figure 2 shows the spatio-temporal characteristics of a sample disk trace. Both types of characteristics should be captured by workload descriptions.

Figure 2: A sample disk trace extracted from cello92. The top graph shows the trace margin on arrival time, that is, the number of requests per 10 seconds, and the left graph shows the trace margin on disk block numbers, that is, the number of requests aggregated by 1000 disk blocks. The irregular shape of the curves suggests strong temporal burstiness and skewed popularity of disk blocks. The bottom right graph shows the trace's projection on the two-dimensional space of arrival time and disk blocks. The clusters of requests in the middle indicate a strong correlation between the two dimensions.

We design the entropy plot metric to quantify both types of characteristics. Entropy is designed to quantify the irregularity of a probability distribution function. We apply it to I/O workloads to quantify burstiness and correlations. In particular, the entropy plot plots the entropy value against the aggregation level of the entropy calculation. For example, to quantify the temporal burstiness, we divide the entire length of arrival time into 2^n intervals of equal length at scale n and calculate the entropy value H_n using the probability that a request arrives with each interval. Plotting H_n against n gives the entropy plot on arrival time. Similar calculation can be done on the trace margin on disk block numbers and can be extended to the two-dimensional projection.

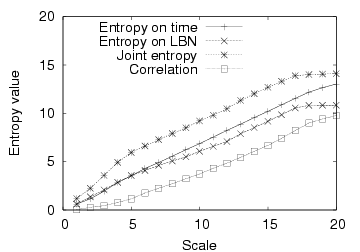
Figure 3. Entropy plot of the sample disk trace.

Figure 3 shows the entropy plot on arrival time, disk block number, and the joint entropy on the both dimensions. First, we observe linear entropy plots, suggesting a consistent level of burstiness and correlation at all scales. This is consistent with previous observation of self-similarity in I/O workloads. Second, the slopes of the one-dimensional entropy plot is smaller than 1, indicating a strong burstiness/skew. We use the slopes to characterize the temporal burstiness and skew in disk block popularity. Third, the correlation between arrival time and disk block numbers is the difference between the sum of the two one-dimensional entropy plots and the joint entopy. The correlation plot is also linear and has a slope larger than 0, suggesting strong correlation between the two dimensions

In summary, the entropy plot takes advantage of the self-similarity of I/O workloads and is able to capture the spatio-temporal behavior with three scalars.

Our approach views device behavior as a function of workloads, and uses a special kind of machine learning tools, regression tools, to approximate the function. Such tools are designed to model functions on multi-dimensional space given a set of samples with known output. Our work chooses to use Classification And Regression Trees (CART) because of its accuracy, efficiency, and interpretability.

We provide two ways to apply CART. A request-level model represents request as a vector, also known as the ``request description,'' and uses the CART models to predict per-request response times. The aggregate performance is then calculated by aggregating the response times. A workload-level model, on the other hand, represents the entire workload as a vector, or the ``workload description,'' and predicts the aggregate performance directly from the workload description.

There is a clear tradeoff between the request-level and workload-level device models. The former are fast in training and slow in prediction, and the latter work the other way around. We will also investigate the possibility of combining the two approaches to build hybrid models that are efficient in both training and prediction.

Training workloads determine the quality of the constructed device models. The training workloads should cover a wide range of workloads in order for the constructed models to predict the performance of an arbitrary workload. Table 1 lists three options in training workload generation.