Motion Planning HW3

Ross Hatton

Date: September 24, 2007

Figure 1: Robot has successfully found a path to the goal. Video 1 . Video 2.

Figure 2: Robot has determined there is no path to the goal. Video 1.Video 2.

Matlab files

Code description

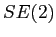My code implements the A$^\star$ algorithm for a rectangular robot with $SE(2)$ configuration space. Figure 1 and the accompanying movie show the robot reaching the goal, along with the $\mathbb{R}^2$ components of the configuration tree searched while finding the path. Note that once the robot reached the lower middle cell, it could have rotated and moved directly into the goal cell. The rotation cost is high enough, however, that the planner instead moves into the right-hand cell, such that it can reach the goal without any additional rotation.

Figure 2 shows the tree searched by the robot before its determination that the goal cannot be reached.

The main routine for the implementation is in the files motion_planning_HW4_success.m and motion_planning_HW4_failure.m. The initial code sets up the robot and the walls, using my object-structure framework. The configuration space is discretized into a three-dimensional grid. There are then 5 individual blocks of code which can be turned on or off individually through the arguments to the main files:

rebuild_cspace

constructs the obstacle table for the configuration space. At each configuration, the robot is collided with all potential obstacles it could intersect, and configurations which result in collisions are flagged.

rebuild_graph

takes the grid form of the configuration space and builds it into a graph with the properties necessary for the A$^\star$ search. The tree is based on 10-point connectivity, with 8-point on the $\mathbb{R}^2$ component and 2-point in the rotational component, with the rotational connectivity wrapping around. The heuristic value is taken as the Euclidean distance from the node to the goal, with the same rotation-to-translation scaling factor used for the edge costs.

research_graph

uses the A$^\star$ algorithm to search the resulting graph. The algorithm is the same as that presented in the lecture notes, except that the algorithm will also exit if the only open nodes are obstacles (otherwise, the obstacles would eventually be plowed through).

calc_path

takes the searched tree and uses the backpointers to determine both the path found for the robot and the plot lines for all positions tried.

animate_path

Draw the tree searched and animate the successful path.