Uniprocessor implementation notes
This document describes the state of the QM implementation and
datastructures as of Milestone 1. Some aspects, in particular the
table datastructures, are not optimally designed for our purposes
and may be changed in the future.
1 Datastructures
The two major datastructures needed for uniprocessor QM are
implicants and tables of implicants. Implicants are bit vectors
that, in some hypothetical circuit, should produce "true" or
1 as output. However, in addition to 1s and
0s, the vectors also have to represent -s, which
are "don't care" bits. For example, the implicant 11-
means that both 111 and 110 inputs would produce
a 1 as output. Having - bits is important to
allow us to discover how to reduce the number of required
implicants.
We also use tables of implicants. The first table of
implicants is the input list of all implicants for a given
circuit. On each iteration of the algorithm, a reduced list of
implicants is produced by finding all pairs of implicants that
differ in only one bit. This particular bit is changed to a
- in the new list.
1.1 Implicants
Since QM often compares implicants to try to find ones that differ
by only one bit, it is important for this comparison to be fast.
Our implicant representation is designed with this in mind.
1.1.1 Structure
An implicant structure contains two dynamically allocated
"vectors" of bit strings; each unit in these vectors is a long
long unsigned int, and bits are stored in little-endian order.
One vector, named dashes, represents -s. The
other, logic, represents actual logic values of
0 or 1 in the implicant; that is,
non--s. Representation invariants are as follows:
- If a bit in dashes is 1, then that bit of
the implicant is a -, and the corresponding bit in
logic must be 0.
- If a bit in dashes is 0, then the
corresponding bit in logic represents the actual logic
value.
- Any unused bits (i.e., internal fragmentation) in the
datastructure must be 0.
The datastructure also keeps track of the number of terms in
the implicant, the number of vector units required to store that
many terms (this should be considered private), and another value,
used. On initialization, used is 0. It is used
for the QM algorithm, not for any internal implicant bookkeeping,
so it will be discussed later in the document.
1.1.2 Operations
Basic operations for creating, destroying, assigning, and
duplicating implicants exist, and generally run in time linear
with the size of the datastructure. The more interesting
operations are implicant_diff0 and, especially,
implicant_diff1.
The purpose of implicant_diff0 is to check whether two
implicants have the same value. It accomplishes this simply by
xoring each pair of corresponding logic and
dashes vector units in turn, and oring the
logic and dashes xor comparison results
together, until it either reaches the end (which means they are
equal) or it gets a non-zero result (which means they are not.)
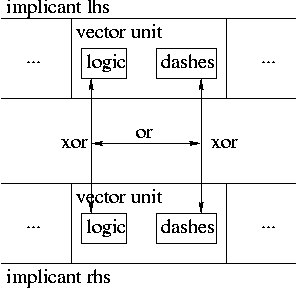
Comparison between corresponding units of two implicants
implicant_diff1 does the same
or-of-xor for each corresponding vector unit
pair, but uses it differently. If the resulting value is a power
of 2 (which can be determined using a bitwise and with
said value minus 1), then there was a difference between the units
in exactly one place (explanation to follow at some point). If
there is exactly one such difference between units, then there is
exactly one difference overall; as we shall see, this is useful in
generating the next table of implicants to work on.
1.2 Tables
Tables are resizable datastructures, basically vectors, containing
some number of implicants. In each iteration of the algorithm,
implicants from the source table are reduced through
implicant_diff1 into another table; prime implicants are
then collected from these tables into a new table that will become
the source table on the next iteration. Operations on tables
include creation, destruction, adding implicants (with or without
checking for duplication), and some I/O operations. These are not
especially interesting; one issue is that adding without
duplication uses implicant_diff0 and is slow. To speed
this up, a datastructure with easier location of existing members
would probably help, if the number of implicants were large.
Alternatively, it may work not to check for duplicates at all.
2 Algorithm
The algorithm is exactly the one described in the proposal. On
each iteration, we use implicant_diff1 to find all pairs
of implicants in the table that differ in exactly one bit. These,
along with any prime implicants in the source table (i.e., ones
that differ in more than one bit), are saved to become the new
table for the next iteration. Once implicant_diff1 finds
no more matches, the table contains only prime implicants.
Because finding the number of pairs in a table is quadratic in the
size of the table times linear in the size of its implicants, for
large tables this does take a reasonably long time.
3 Timing results
We timed the uniprocessor implementation on tables with 1 to 8 or
12 implicants, and both 2^n and 2^(n-1) elements. The former
tables, containing all possible implicants for the given number of
terms, always reduce to having 0 prime implicants, and should give
a very regular progression of runtimes. As it turned out, they
do:
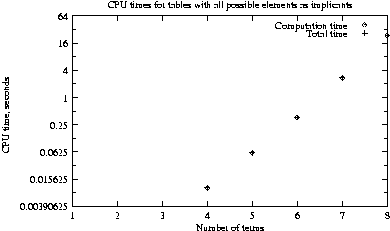
We use a lg scale for the y axis, since the input table size is
actually growing exponentially in the number of terms. The
runtime appears to be linear, which seems very good given the
necessity of comparing all pairs of implicants at each iteration.
The other test we tried was on table with half of the possible
number of implicants, randomly selected. As expected, this gave
slightly less regular results, and ran a bit faster (hence the
larger upper bound on the number of terms tested), although the
asymptotic time still seems to be linear:

4 Possible improvements
As mentioned, we may go for a different table representation to
speed up non-duplicating additions, or we may modify code
elsewhere such that duplications do not matter. If we do the
latter, implicant_diff0 will not be necessary, at least
as far as we know at present. If we do the former, overhead will
probably increase so that it would be less worthwhile for small
datasets. On the other hand, small datasets may be somewhat
doomed in this respect (excessive overhead) for multiprocessor
computation anyway.



