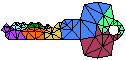I have written a chain of software tools, collectively known as
Archimedes
(illustrated at right),
to automate the process of creating large-scale finite element simulations.
(The finite element method is a numerical method for approximating
solutions to partial differential equations, and can simulate a wide variety
of physical phenomena, including fluid flow, heat transfer, and
electromagnetic wave propagation.)
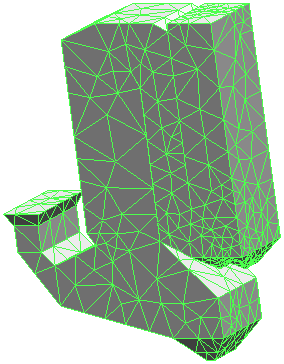The most challenging task to automate, and the topic of my dissertation,
is the generation of high-quality unstructured finite element meshes,
such as the tetrahedral mesh of a tire incinerator illustrated at left.
The development of sophisticated mesh generators has been essential
for the success (and even the viability) of the Quake Project.
Here I discuss four of the results of my research. I describe Archimedes briefly; then I detail the algorithms employed in the two mesh generators of the Archimedes toolchain. I conclude with summaries of two results that arise from my mesh generation work, and are also of independent interest: a method of guaranteeing numerical robustness, and a basic result in the geometry of triangulations.
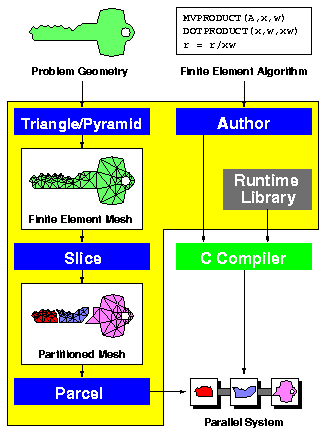
Scientific software: Archimedes.
The Archimedes toolchain
is composed of two mesh generators, named
Triangle and Pyramid;
a geometric mesh partitioner called Slice,
which divides a mesh into subdomains
that may be modeled on separate processors;
Parcel, which computes communication schedules and
rearranges global data sets into a form suitable for multiple processors;
and Author (written in collaboration with David O'Hallaron),
which generates parallel code for finite element simulations,
based on machine-independent, communication-concealing
application code written by scientific users.
Archimedes created the Quake Project's
simulations of ground motion in the San Fernando Valley,
which are among the largest unstructured physical
simulations ever performed,
with meshes of up to 77 million tetrahedra.
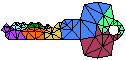
Mesh generation.
Mesh generation is the most difficult task to automate
because a mesh must satisfy nearly contradictory requirements:
it must conform to the shape of the simulated object;
it must be composed of elements (triangles or tetrahedra)
that are of the right size and shape, avoiding extreme angles;
it may have to grade from small to large elements over a relatively
short distance.
Commercial mesh generators have proven unsuitable for the Quake Project's needs, because most of them generate poor-quality elements, and all of them break down at problem sizes a hundred times smaller than those we are working with now. Mesh generation is so inherently complex that any meshing algorithm is likely to be foiled by input geometries having small features, small angles, or complicated topologies, unless the algorithm's results are theoretically verifiable.
Fortunately, this decade has brought about two-dimensional Delaunay refinement algorithms that not only work well in practice, but have provable bounds on element quality and mesh grading. Part of my work has been to remove the last barrier to the practicality of these algorithms - their tendency to fail in the presence of small input angles - by proposing (and proving the effectiveness of) a modification that ensures that they always produce a valid mesh, and that the quality of the mesh degrades gracefully as the input degrades.
My mesh generator Triangle is an industrial-strength implementation of two-dimensional Delaunay refinement, and has been freely available to the public for several years. Triangle has thousands of users, with applications ranging from radiosity rendering and terrain databases to stereo vision and image orientation, as well as dozens of variants of numerical methods. Triangle has been licensed for inclusion in seven commercial programs, for purposes ranging from ocean floor database interpolation to cartoon animation.
My central results, however, are provably good three-dimensional mesh generation algorithms based on Delaunay refinement. The jump from two dimensions to three is surprisingly difficult, and is impeded by fundamental geometric limitations (see the paragraph below labeled ``Geometry''). Nonetheless, one of my algorithms provably generates a nicely graded mesh whose tetrahedral elements have circumradius-to-shortest edge ratios bounded below 1.63. Unlike previous provably good tetrahedral mesh generation algorithms, my algorithm can mesh general straight-line nonmanifold domains with holes, interior boundaries, and dangling edges and facets.
These theoretical results ensure that most types of bad tetrahedra cannot appear in the mesh, but do not rule out the possibility of a bad tetrahedron known as a sliver. Fortunately, Delaunay refinement algorithms outperform their worst-case bounds in practice. Pyramid, my implementation of three-dimensional Delaunay refinement, can usually generate meshes of tetrahedra whose dihedral angles are bounded between 20o and 150o (including the tire incinerator mesh above). I expect to release Pyramid to the public in 1998, giving researchers free access to tetrahedral mesh generation facilities that in some ways surpass commercial programs.
Numerical robustness.
Unfortunately, many implementations of fine geometric algorithms
hang, crash, or produce nonsensical output
because of the cruelty of floating-point roundoff.
I have treated the problem extensively, taking the following three steps.
First, I have developed fast software-level algorithms for
exact arithmetic on arbitrary precision floating-point values.
Second, I have proposed a technique for adaptive-precision arithmetic that
speeds these algorithms in calculations that need not always be exact,
but must satisfy some error bound.
Third, I have used these techniques to implement
robust geometric predicates.
The predicates are adaptive; their running times depend on the degree
of uncertainty of the results, and they are usually almost as fast as
nonrobust predicates.
Triangle and Pyramid both use these robust predicates, which have been indispensable in allowing the Quake Project to generate very large meshes that had previously been unattainable because roundoff errors had caused the mesh generators to fail. The consistent (but fast) performance that my adaptive-precision arithmetic provides has bolstered Triangle's popularity in the research and commercial communities.
Geometry of triangulations.
My mesh generation research has engendered a
fundamental geometric result of independent interest.
A geometric structure known as the constrained Delaunay triangulation
is useful for many two-dimensional geometric problems,
including mesh generation and the interpolation of discontinuous functions,
but has heretofore evaded any attempt
to generalize it to higher dimensions.
A major hurdle is the fact that not all polyhedra
can be tetrahedralized without additional vertices;
furthermore, it is NP-hard to determine whether or not a
polyhedron can be thus tetrahedralized, or how many additional
vertices must be added to make it possible.
I have shown that one may construct a constrained Delaunay tetrahedralization that conforms to a set of planar facets in E3 if for each segment s on the boundary of each input facet, s is contained in a ball that contains no vertex other than the endpoints of s. In other words, if you want to form the constrained Delaunay tetrahedralization of a set of polyhedral facets, and are willing to insert enough additional vertices to force all of the segments to appear in the (unconstrained) Delaunay tetrahedralization, then you can force the tetrahedralization to conform to the facets at no additional vertex cost. This result generalizes straightforwardly to higher dimensions. It provides a new insight into a fundamental geometric structure, and is also an invaluable aid in deriving stronger results for my tetrahedral mesh generation algorithm.
