. numerator not 0 for l=1 and n 
1.
Approximation gives: 
. No coupling to 
so can ignore spin. In the ground state 
so 
.
For the ground state, this is 0 to first order.
In second order, you get: . numerator not 0 for l=1 and n 1.
Approximation gives:
= quadratic stark effect. Polarization= 
. Polarizability= 
polarization.
This is 
. Actual calculation gives 
which agrees well with experimentation.
For excited states:
For n=2, there is 8 fold degeneracy
With spin orbit coupling, you get a 6 fold degeneracy on 
.
Weak fileds - non-degenerate P.T. = 2nd order quadratic.
Strong fields, then 2s and 2p are degenerate.
. Constructing a 4x4 matrix, you get:
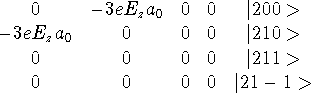. Diagonilizing, you get: the roots, 0,0, 
. The eigen states are
, 
. This is the linear stark effect. Only shows up for strong fields,
when lamb shifts and spin orbit coupling are neglectable. This means
.