The laplacion is .

This is simple in a rectangular basis. It can be found in arbitrary basis by playing with partials. This is pretty messy.

Another method for orthogonal coordinate systems:

Let and . Then the coordinates are orthogonal if satisfy .

The length element in the new coordinate system is . So .

For spherical coordinates,

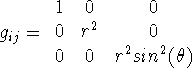. Define .

For volume integrals, where .

For the gradient: The inverse matrix is needed so, so gradient =

For divergence:

source psfile jl@crush.caltech.edu index spherical_coordinate_green_function laplacian_eigenfunction_expansion