


Next: Future Work
Up: Summary of Completed Work
Previous: The Simulations and
For long wavelengths and at large distances related to source dimension,
earthquakes, especially aftershocks, may be approximated by point
sources [2]. We have successfully incorporated a point source model
in our finite-element analysis and implemented it into our FEM simulation
code. To verify the effectiveness of this point source model, we compared
our results for the so-called transparency case, i.e., homogeneous half-space
with a point source, with those from the Green Function solution
[20] which is an analytical solution in this case. The results
from the two methods agreed very well, as can be seen in Figure 3, which shows
the responses at a given location on the ground in north-south(N-S),
east-west(E-W) and vertical(U-D) velocity components on the first, second
and third rows, respectively. Responses at other locations show the similar
agreement between the two different methods.
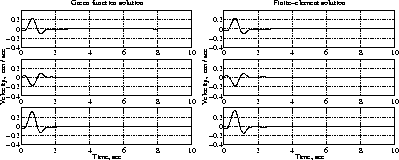
Figure 3: For the transparency case, the comparison of results from our FEM computation with those from the Green function shows basically identical responses at a observation locations. The first, second and third rows show the velocity
components at a given location on the ground in north-south(N-S),
east-west(E-W) and vertical(U-D), respectively.
Next we chose one of the 1994 Northridge earthquake aftershocks in the San
Fernando basin as our first simulation of a realistic case. The aftershock data
are listed in Table 2.

Table 2: The aftershock event information
We use a 3-D elastic model of the San Fernando basin provided by Magistrale
et al [31], in which the minimum S-wave velocity is 0.2
km/s, the lowest to date in 3D numerical simulations. Figure 4 shows the distribution of S-wave velocity near the free surface of the San Fernando basin.

Figure 4: Surface distribution of S-wave velocity in the San Fernando basin. Epicenter of the aftershock is indicated by an x.

Figure 5: Distribution of maximum surface horizontal velocity in the San Fernando basin.
In this mesh, 76,778,630 high quality tetrahedron elements are generated by
unstructured adaptive meshing [3] to assure stability and
accuracy. The Archimedes tool chain was used to implement the simulation,
pre-process and code. To
solve 40,267,689 linear equations, the computation was performed with 256
processors on the T3D parallel computer at the Pittsburgh Supercomputing
Center.
We have obtained reasonable results, and the initial analysis of the results
has shown very strong local site effects, as can be seen in Figure 5, which
shows the distribution of the maximum ground surface horizontal velocity.
This result reflects well the surface distribution of S-wave velocity by
comparing it with Figure 3. Maximum response tends to occur near interfaces
between softer and harder materials. The highest maximum velocity is about
40 times larger than that at the outcrop although the contrast of S-wave
velocity is only about 6 times higher.



Next: Future Work
Up: Summary of Completed Work
Previous: The Simulations and
Hesheng Bao
Mon Mar 24 21:08:34 EST 1997



