15-212-ML : Homework Assignment 3

Maximum Points: 100 (+30 extra credit) 

Guidelines

• Strive for elegance! Not every program which runs deserves full credit. Make sure to state invariants in comments which are sometimes implicit in the informal presentation of an exercise. If auxiliary functions are required, describe concisely what they implement. Do not reinvent the wheel and  try to make your functions small and easy to understand. Use tasteful layout and avoid longwinded and contorted code.
• Make sure that your file compiles and runs. A program which doesn't run will not get full credit and is likely to incur a heavy penalty.
• Home works must be all your own work.
• Late home works will be accepted only until start lecture on Thursday, with a 25% penalty.
• If you have any questions about this assignment, contact Philip Wickline at  philipw@cs.cmu.edu, Adam Megacz at megacz@usa.net , or use cmu.andrew.academic.cs.15-212-ML.discuss.

Problem 1: Dictionaries (35 points + 10 extra credit)

However, without taking special care, trees that are built from arbitrary insertions of data are not necessarily balanced, meaning that searches may take time O(n) in the worst case. There are many mechanisms for building balanced binary search trees. One such mechanism, red-black trees, is described in the lecture notes. For problem 1 you will implement balanced binary trees using a balancing criterion based upon tree height.

We define the height, h(t), of trees inductively on the structure of the tree:

h(empty) = 0
h(t) = 1 + max(h(t.left), h(t.right))

The idea is to store at each node the height of that node in the tree. Then, when new trees are constructed from old trees, the new tree can be balanced by means of one of the rotations described below. In addition to the binary search tree invariant described above, you must maintain the following invariant at each node with height greater than 2:

where w is a constant called the weight ratio, l is the left child, and r is the height of the right child. In other words, at every node, neither child is more than w times the height of the other.

There are four rotations that you will use to keep trees balanced: single left, single right, double left, and double right. The two left rotations are presented pictorially below; the right rotations are just the mirror images of these.

 
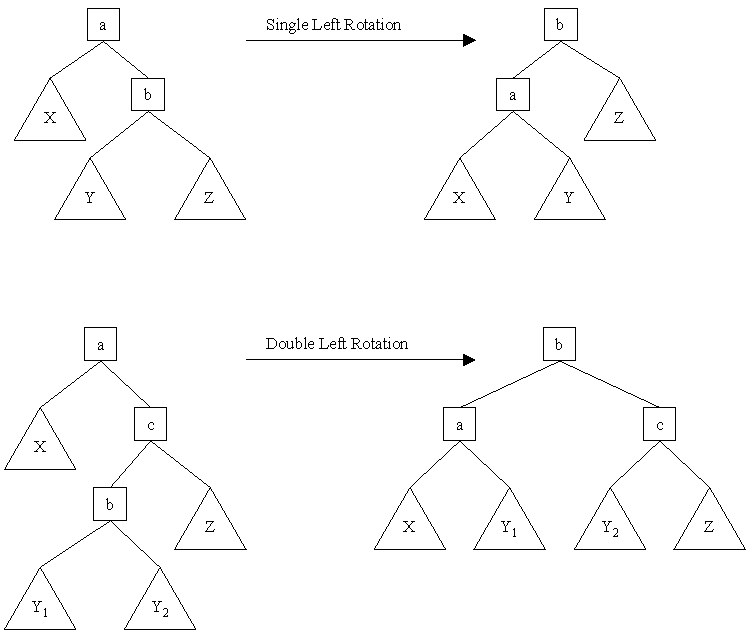
A single rotation lifts Z relative to X and Y, while a double rotation lifts Y. Therefore, when balancing trees, you should use a double rotation if Y is taller, or a single rotation if Z is taller.
 

Question 1.1 (35 points)

signature DICT =
sig
  type key = string
  type 'a entry = key * 'a
  type 'a dict

  val empty : 'a dict
  val lookup : 'a dict * key -> 'a option
  val insert : 'a dict * 'a entry -> 'a dict
  val fold : ('a * 'b * 'b -> 'b) -> 'b -> 'a dict -> 'b

(*val delete : 'a dict * key -> 'a dict (* extra credit *) *)
end;  (* signature DICT *)

Use w = 3 and use the following datatype as the representation type of an 'a dict.

datatype 'a dict =
    E
  | T of 'a entry * int * 'a dict * 'a dict; (* data * height * left child * right child *)

(* Invariants (writing height(t) for the height of tree t):
   1. t : s dict is a binary search tree
   2. For every tree t = T (e, h, left, right), h = height(t)
   3. For every tree t = T (e, h, left, right),
      height(left) <= w*height(right) and height(right) <= w*height(left)
*)

• empty should be the empty tree
• lookup (tree, key) should return SOME of the value associated with key in tree if it is in the tree, and NONE otherwise
• insert (tree, (key, value)) should take a balanced tree tree and an entry (key, value) and return a balanced tree with the new entry in it. If key already exists in the tree, the old entry should be replaced with the new.
• fold f init d should go through the binary tree d and return init if it encounters a leaf (i.e. the empty tree). For every other node in the tree it should return f(datum,vLeft,vRight) where datum is the datum of the node, and vLeft is the result of applying fold on the left subtree of d, vRight is the result of applying fold on the right subtree of d.

Hint: Your code will be much easier to understand if you use a helper function balance (not visible in the signature!) which takes an entry a and two balanced trees, X and Y, whose heights are not too much out of balance (you need to decide how much that is, it will be an invariant of the function), and constructs the balanced tree derived from the tree

using one of the rotations, if necessary. Again, be sure to state all of the invariants balance expects from its arguments.

 Question 1.3 (Extra Credit, 10 points)

Problem 2: An Address Book (30 points)

The following signature ADDRESSBOOK describes address books:
 
signature ADDRESSBOOK =
    sig
        type key = string
        type entry =
            {Key : key,
             LastName : string,
             FirstName : string,
             Nickname : string option,
             Email : string,
             OfficeBuilding : string,
             OfficeNumber : int}
        type address_book

        val empty : address_book
        val addEntry : address_book * entry -> address_book
        val lookup : address_book * key -> entry option

        exception NotFound of key
        val updateNickName : address_book * key * string -> address_book
        val updateEmail : address_book * key * string -> address_book
        val updateOfficeBuilding : address_book * key * string -> address_book
        val updateOfficeNumber : address_book * key * int -> address_book
       (* question 2.2 & 2.3 *)
        val getRange address_book * key * key -> entry list
    end

The address book will store entry records with information about the people listed in the address book.  The entries should be stored with the concatenation of the last name and the first name as keys. For instance the entry with LastName = "Wickline" and FirstName = "Philip" should have Key = "WicklinePhilip", and should be stored with key "WicklinePhilip" in the collection of entries.

Question 2.1 (10 points)

• empty should be the empty address book
• addEntry(book, entry) creates a new address book extending book with the key #Key entry mapped to entry
• lookup(book, key) returns SOME of the entry associated with key in book, if one exists, and NONE otherwise
• updateFoo(book, key, value) should return a new address book which is identical to book except that the Foo field of the record associated with key contains value. If key does not occur in book, then the exception NotFound key should be raised.

Question 2.2 (10 points)

Question 2.3 (10 points)

Problem 3: Regular expressions (35 points + 20 extra credit)

• Characters a
• Concatenation r₁ r₂
• The empty string One
• Alternative r₁ + r₂
• Empty set Zero
• Repetition r^*

datatype regexp =
    Char of char
  | Times of regexp * regexp
  | One
  | Plus of regexp * regexp
  | Zero
  | Star of regexp;

• A wildcard symbol _ which accepts any character
L(_) = {a | a is a character in the alphabet} The constructor must be called Underscore.
• Intersection r₁ & r₂ which accepts a string only if it is contained in r₁ and simultaneously in r₂.
L(r₁ & r₂) = {s | s in L(r₁) and s in L(r₂)} The constructor must be called And.
• A wildcard T which matches any string.
L(T) = {s | s is a string over the alphabet} The constructor must be called Top.
• Negation ~  r which contains every string which is not contained in r.
L(~ r) = {s | s not in r} The constructor must be called Not.

Question 3.1 (5 points)

Question 3.2 (15 points)

Question 3.3 (15 points)

Question 3.4 (Extra credit, 10 points)

Question 3.5 (Extra credit, 10 points)

Handin instructions

• Put your SML code into a single file named ass3.sml in your ass3 directory. All of your definitions should be in this one file. Please keep a backup for your records. Your handin directory for this assignment is
/afs/andrew/scs/cs/15-212-ML/studentdir/<your andrew id>/ass3/ass3.sml