CS 15-212-ML: Assignment 2

Due Wednesday, September 23, 12:00 noon (electronically); papers at recitation.

Maximum Points: 100 (+10 extra credit)

Guidelines

Strive for elegance! Not every program which runs deserves full credit. Make sure to state invariants in comments which are sometimes implicit in the informal presentation of an exercise. If auxiliary functions are required, describe concisely what they implement. Do not reinvent wheels and try to make your functions small and easy to understand. Use tasteful layout and avoid longwinded and contorted code. None of the problems requires more than a few lines of SML code.
Make sure that your file compiles and runs. A program which doesn't run will not get full credit and is likely to incur a heavy penalty.
Homeworks must be all your own work.
Late homeworks will be accepted only until start lecture on Thursday, with a 25% penalty.
If you have any questions about this assignment, contact Doug Fearing at fearing@andrew.cmu.edu, Mark Plesko at mp5f@andrew.cmu.edu, or use cmu.andrew.academic.cs.15-212-ML.discuss.

Problem 1: Fibonacci Trees (35 pts)

Leonardo da Pisa, son of Bonacci, better known as Fibonacci ("Filius Bonaccii") is nowadays well-known mainly to mathematicians and computer scientists for the sequence of numbers that bear his name:

f₀ = 1

f₁ = 1

f_n+2 = f_n+1 + f_n

One of his major concerns in life (1180-1250) were, however, rabbits. In particular, he was interested in knowing how rabbits reproduce and, assuming to start with one male and one female rabbit, how many rabbits he would get after any fixed amount of time. For this purpose, he came up with the following (admittedly approximate) discrete model of rabbit reproduction:

A couple of adult rabbits engenders another couple of rabbits every month
(thus the stimulus for a popular American cliche);
it takes exactly one month for a young rabbit to become adult.

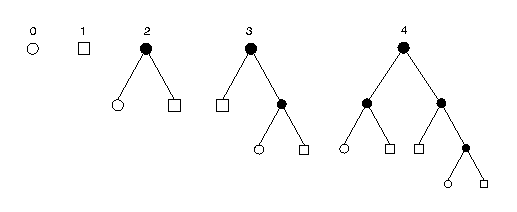
Starting from one couple of young rabbits, the evolution of the rabbit population can be represented by the infinite sequence of Fibonacci trees of which the first five elements are as follows:

Each leaf in the tree represents a rabbit couple. A couple of young rabbits is represented as an empty circle, while a couple of adults is pictured as a square. Internal nodes contribute to the tree structure and can serve the purpose, for example, of computing the age of the rabbits.

The n-th element of this sequence, that we will denote as T_n, is a snapshot of the rabbit population at month n.

Question 1.1 (10 pts)

Given the following declaration describing the structure of Fibonacci trees

datatype fibTree = Young | Adult | Node of fibTree * fibTree

write an SML function nextFibTree, of type fibTree -> fibTree, that, given an object of type fibTree, creates a new fibTree of the next generation according to Fibonacci's specification of rabbit reproduction, as exemplified in the figure above.

Use nextFibTree to write a function createFibTree of type int -> fibTree that, given a natural number n, generates T_n. You may assume that n >= 0, but please document this in an invariant in your code.

Question 1.2 (10 pts)

An interesting property about Fibonacci trees is that for any natural number n, T_n+2 is a binary tree having T_n as its left subtree and T_n+1 as its right subtree. This is illustrated in the picture below.

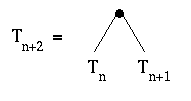On the basis of this property and of examples shown in class, devise an efficient implementation of the function createFibTree' performing the same task as the function createFibTree from the previous question. This function should minimize redundant computation. Carefully state and prove its correctness.

Question 1.3 (15 pts)

Write an SML function countFibTreeLeaves, of type fibTree -> int, that returns the total number of leaves of the given Fibonacci tree. Notice that on the tree T_n, this is the number of rabbit couples in the n-th month.

Prove the following mathematical property about Fibonacci trees:

the total number of leaves of T_n is f_n;
for any natural number n, T_n+2 contains f_n nodes corresponding to couples of young rabbits (circles in the figure above), and f_n+1 leaves corresponding to adult couples (squares above).

Problem 2: Sets and Relations (25 pts)

Sets play an important role as the foundation of most areas in Mathematics. Mathematicians enjoy working with extremely large sets, far beyond infinity. Sets are also a useful form of abstraction in Computer Science, although they are seldom used in practice due to their high manipulation overhead. Ways to implement certain countable (i.e. mildly infinite) collections of data will be described further on in the course. In this exercise, we will instead concentrate on finite sets, related concepts (relations and graphs), and their use in a small application.

Question 2.1: Finite Sets (15 pts)

We consider a simple implementation of the set data structure based on the list type of SML. The following declaration serves this purpose:

type 'a set = 'a list

Lists can be exploited in different manners as a support to the representation of sets. The choice is left entirely to you: what matters is that the functions you are requested to implement manifest their expected behavior.

For this assignment we assume that the elements of the set belong to an equality type, that is, elements x and y can be compared with the expression x = y. You may wish to consult Paulson, Section 3.14: Equality Types, for more information.

Give a correct implementation of a structure Set :> SET that satisfies the following signature (accessible in the file ass2.sml in this assignment's directory)

signature SET =
sig

  (* types *)
  type 'a set

  (* exceptions *)
  exception NotFound

  (* constants *)
  val empty : ''a set

  (* conversions *)
  val toList : ''a set -> ''a list
  val fromList : ''a list -> ''a set

  (* single set operators *)
  val insert : ''a * ''a set -> ''a set
  val remove : ''a * ''a set -> ''a set
  val isEmpty : ''a set -> bool
  val filter : (''a -> bool) -> ''a set -> ''a set
  val map    : (''a -> ''b) -> ''a set -> ''b set
  val member : ''a * ''a set -> bool

  (* binary set operators *)
  val union : ''a set * ''a set -> ''a set
  val intersection : ''a set * ''a set -> ''a set
  val difference : ''a set * ''a set -> ''a set
end;

and the specifications below for the values it mentions

empty is the value representing the empty set.
toList s returns a list containing all the elements of s without duplications.
fromList l returns a set containing all the members of l.
insert (x, s) inserts x in s and returns the augmented set.
remove (x, s) removes x from sand returns the reduced set. If x does not belong to s, the exception NotFound is raised.
isEmpty s tests whether s is empty.
filter p s returns the set of the members of s on which p evaluates to true.
map f s returns the set of values obtained by applying f to the members of s.
member (x, s) tests whether x is contained in s.
union (s1, s2) computes the union of s1 and s2.
intersection (s1, s2) computes the intersection of s1 and s2.
difference (s1, s2) computes the set difference of s1 and s2. The set difference of s1 and s2 is defined as all the elements of s1 that do not occur in s2

Question 2.2: Relations (10 pts)

A binary relation is a set having ordered pairs of objects as its elements. The set of objects that are allowed as the first components of these pairs form the domain of the relation. Similarly, the elements that can appear as the second component of the pairs form its codomain.

On the basis of this definition, the representation of relations is immediate:

type ('a, 'b) relation = ('a * 'b) Set.set

Use the operations contained in the structure Set you just wrote in order to define the structure Rel implementing some basic operations on relations, as specified by the following signature (file ass2.sml in this assignment's directory):

signature RELATION =
sig

  (* types *)
  type ('a, 'b) relation = ('a * 'b) Set.set

  (* operators *)
  val image : ''a * (''a, ''b) relation -> ''b Set.set
  val preimage : ''b * (''a, ''b) relation -> ''a Set.set
  val diagonal : ''a Set.set -> (''a, ''a) relation
end;

These operations ought to realize the following functionalities:

image (x, r) returns the set of ys such that (x,y) is an element of r.
preimage (y, r) returns the set of xs such that (x,y) is an element of r.
diagonal s returns the relation r consisting of the pairs (x, x) such that x belongs to s.

Problem 3: Mathematical Expressions (40 Points) (+10 pts extra credit)

In this part of the assignment, we will introduce a representation of mathematical expressions of one variable, x, using the datatype:

datatype mexp =             (* m        *)
    X                       (* x        *)
  | Real of real            (* r        *)
  | Sin of mexp             (* sin( m ) *)
  | Cos of mexp             (* cos( m ) *)
  | Exp of mexp             (* e^m      *)
  | Power of mexp * real    (* m^r      *)
  | Plus of mexp * mexp     (* m1 + m2  *)
  | Times of mexp * mexp    (* m1 * m2  *)

In this format the function 1 + x^2 + sin( e^x ) could be represented in many ways; two examples are:

Plus(Real(1.0), Plus(Power(X, 2.0), Sin(Exp(X))))

Plus(Plus(Real(1.0), Times(X, X)), Sin(Exp(X)))

Question 3.1 (25 pts)

Implement a structure MathExp :> MATHEXP.

All of the functions should be evident from their names (i.e., real 6.0 => Real(6.0)) The derivative function should return a mathematical expression that is the symbolic derivative of the argument. The transform function takes a mathematical expression and returns its implementation as an ML function. The evaluate function should evaluate a mathematical expression at a given real.

signature MATHEXP =
sig

  (* types *)
  type mexp

  (* building blocks *)
  val x : mexp                         (* x         *)
  val real : real -> mexp              (* r         *)
  val sin : mexp -> mexp               (* sin( m )  *)
  val cos : mexp -> mexp               (* cos( m )  *)
  val exp : mexp -> mexp               (* e^m       *)
  val power : (mexp * real) -> mexp    (* m^r       *)
  val plus : (mexp * mexp) -> mexp     (* m1 + m2   *)
  val times : (mexp * mexp) -> mexp    (* m1 * m2   *) 

  (* operations *)
  val derivative : mexp -> mexp
  val transform : mexp -> (real -> real)
  val evaluate : (mexp * real) -> real
end;

Recall the trigonometric differentiation rules
(d/dx)(sin x) = cos x and (d/dx)(cos x) = - sin x.
Especially important is the chain rule: (f(g(x)))' = f'(g(x))g'(x).

Question 3.2 (15 pts)

Prove that your implementation of the derivative function correctly computes a mathematical expression representing the derivative.

Question 3.3 (10+ pts extra credit)

In order to insure that our mathematical expressions do not become overly complex, we could simplify our expressions. To do this, we will reduce any of the following forms:

Exp(Real(0.0))
Power(m, Real(0.0))
Plus(Real(0.0), m)
Plus(m, Real(0.0))
Times(Real(1.0), m)
Times(m, Real(1.0))
Times(Real(0.0), m)
Times(m, Real(0.0))

Add a function simplify : mexp -> mexp to both the signature and structure that reduces these forms. For the purpose of these simplifications, we will allow 0.0^0.0 to evaluate to 1.0. You can gain more points by implementing additional simplifications.

Handin instructions

Put your SML code into a file named ass2.sml in your ass2 directory. Please type your name and recitation instructor in a comment at the top of your file. All of your definitions should be in this one file. You should copy your file to

/afs/andrew/scs/cs/15-212-ML/studentdir/<your andrew id>/ass2/ass2.sml

Hand in your proofs for Question 1.2, 1.3, and 3.2 on paper at the recitation. Please write your name and recitation instructor on all written work.

Last modified: Tue Sep 15 14:40:38 EDT