CS 15-212-ML: Assignment 1

Due Wednesday, September 9, 12:00 noon (electronically); papers at recitation.

Maximum Points: 50 (+10 extra credit)

Guidelines

Strive for elegance! Not every program which runs deserves full credit. Make sure to state invariants in comments which are sometimes implicit in the informal presentation of an exercise. If auxiliary functions are required, describe concisely what they implement. Do not reinvent wheels and try to make your functions small and easy to understand. Use tasteful layout and avoid longwinded and contorted code. None of the problems requires more than a few lines of SML code.
Make sure that your file compiles and runs. A program which doesn't run will not get full credit and is likely to incur a heavy penalty.
Homeworks must be all your own work.
Late homeworks will be accepted only until start lecture on Thursday, with a 25% penalty.
If you have any questions about this assignment, contact Mark Plesko at mp5f@andrew.cmu.edu, Doug Fearing at fearing@andrew.cmu.edu, or use cmu.andrew.academic.cs.15-212-ML.discuss.

Problem 1: Warm-up Exercises (10 pts)

Question 1.1 (3 pts)

Write a function bigEven of type int -> bool that decides whether its integer argument is even and greater than one hundred (100). For example,

bigEven(120)	=>	true
bigEven(135)	=>	false
bigEven(100)	=>	false

Question 1.2 (3 pts)

Write a function oddSum of type int -> int that calculates the sum of the first n odd numbers on input n.

Calculate recursively, i.e. you may not directly calculate n² . You may assume that the input is greater than or equal to 1, but you should document this.

Question 1.3 (4 pts)

Show by induction that oddSum is a correct implementation and computes n². Carefully state the inductive hypothesis and do not omit the boundary condition! You don't need to type your proof in (writing it by hand and handing it in at recitation is usually faster and easier).

Problem 2: Recursion (10 pts) (+10 pts extra credit)

Question 2.1 (5 pts)

Consider the function horner : int * int -> int. The Horner method is an algorithm for the efficient computation of the sum of powers of a number.

      (* horner (x, n) = 1 + x + x² + . . . + xⁿ *)
      (* val horner : int * int -> int *)
      (* invariant : n >= 0 *)
      fun horner (x, 0) = 1
        | horner (x, n) = 1 + x * horner(x, n-1)

Show by induction that the function horner correctly computes the sum of the powers of x from 0 to n.

Question 2.2 (5 pts)

The integer logarithm base b of x is defined as the unique integer n such that

bⁿ <= x < bⁿ⁺¹

Write a function intLog : int * int -> int such that intLog (b, x) recursively computes the integer logarithm of x base b without using the logarithm functions included in the ML basis library. You may assume that b >= 2 and x >= 1, but you should document this. Your function should not use values of type real in order to avoid round-off errors.

Question 2.3 (10 pts extra credit)

Prove that your implementation of intLog correctly computes the integer logarithm as described above.

Problem 3: Numerical Differentiation (15 pts)

In this problem we will discuss and implement a method for numerical differentiation of functions of one argument. Numerical differentiation means that we will look for a good approximation, but not for a "closed form". Naturally, we cannot expect to find the solution with the first approximation, therefore we must calculate a sequence of approximate values, each an improvement over the previous one. The idea behind these approximations is very simple. Consider the graph of a function

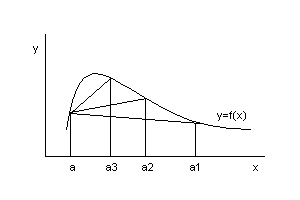
Function Graph

and suppose we wish to calculate the derivative at a. We might start with the approximation

[f(a₁) - f(a)] / [a₁ - a]

and then do likewise with a₂ and a₃. We can hope that as a_i approaches a, our approximation becomes more refined. For the purposes of this assignment, we will use an initial approximation of a + delta, where

delta

is an input to the function. Over each iteration, we will allow our current position to approach a by half the remaining distance. Since we do not have the exact value of the derivative at a, we will accept an approximate value if the absolute value of the difference between the values on the previous and current iterations is less than a given (positive) epsilon.

Question 3.1 (10 pts)

Write an SML function

diff : real * real -> (real -> real) -> real -> (real 
* real)

where diff (epsilon, delta) f a approximates the derivative of f at a up to epsilon starting at range delta. It returns a pair, where the first component yields the current range (remember, we increase our accuracy by halving the range to a on each iteration), and the second the approximate value, as described above. Differentiate

The sine function at pi
The polynomial x² at 3
The exponential function at 1

and check which derivative converges slowest for epsilon = 10^-6 (that is, 0.000001), and delta = 1.0.

Hint: Use the context browser to access information about the mathematical functions from the Math and Real structures. You can access the SML Basis Library for reals at http://portal.research.bell-labs.com/orgs/ssr/sml/real-chapter.html.

Question 3.2 (5 pts)

Now fix epsilon = 10^-6 (= 0.000001) and delta = 1.0 and write a function

diffx : (real -> real) -> (real -> real)

where diffx f is the function g : real -> real which returns the value of the derivative of f on input x.

Problem 4: Newton's Method (15 pts)

We now move to a method for approximating roots of a function. We will again use successive approximations to reach our answer. Given a function f, we first choose initial guess x₀. Once we have guess x_i, we obtain the next guess, x_i+1, by finding the x-intercept of the tangent line to f at (x_i, f(x_i)), as illustrated below:

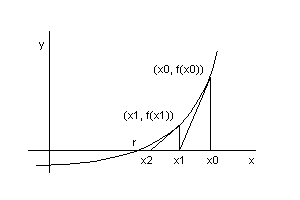
Newton

This is given by the formula

 x_i+1 = x_i - [f(x)/f'(x)]

Question 4.1 (10 pts)

Write an SML function

newton : real -> (real -> real) -> real -> real

where newton epsilon g x approximates a zero of function g up to

epsilon

using initial guess x.

Note: You will need to use your function diffx to solve this problem. You will not be penalized in this question for any errors in your function diffx.

Question 4.2 (5 pts)

Again, fix epsilon = 10^-6 (= 0.000001) and write a function

solve : (real -> real) -> real

where solve f finds a zero of f using initial guess zero.

Handin instructions

Put your SML code into a file named ass1.sml in your ass1 directory. Please type your name and recitation instructor in a comment at the top of your file. All of your definitions should be in this one file. You should copy your file to

/afs/andrew/scs/cs/15-212-ML/studentdir/<your andrew id>/ass1/ass1.sml
Hand in your proofs for Question 1.3, 2.1, 2.3 on paper at the recitation. Please write your name and recitation instructor on all written work.