15-212-X : Homework Assignment 4

Due Wed Oct 22, 2:00pm (electronically)

Maximum Points: 100 (+20 extra credit)

There was a bug in the version of this assignment handed out in class, which has been corrected below. To the see correction only, check the file correction.txt.

Guidelines

Strive for elegance in your code! Not every program which runs deserves full credit. Make sure to state invariants in comments which are sometimes implicit in the informal presentation of an exercise. If auxiliary functions are required, describe concisely what they implement. Do not reinvent wheels and try to make your functions small and easy to understand. Use tasteful layout and avoid longwinded and contorted code. None of the problems requires more than a few lines of SML code.
Make sure that your file compiles and runs. A program which doesn't run will not get full credit and is likely to incur a heavy penalty.
Homeworks must be all your own work.
Late homeworks will be accepted only until start lecture on Thursday, with a 25% penalty.
If you have any questions about the assignment, contact Herb Derby at derby@cs.cmu.edu or use cmu.andrew.academic.15-212-X.discuss.

Please include needed auxiliary declarations from the ML files in /afs/andrew/cmu.edu/scs/cs/15-212-X/assignments/ass4/ in your solution file, so it compiles as is. Points will be deducted if your file does not compile by itself.

Motivation and History

In this assignment, we develop a data structure called a region that plays a fundamental role in the implementation of a graphical windowing system.

A graphical windowing system divides the screen into areas where applications can draw their output. Because windows can overlap, the windowing system must allow drawing within arbitrarily shaped parts of the screen. Windowing systems use regions to represent the visible part of a window.

You can think of the screen as grid of small rectangles (usually more than a million per screen) called pixels. Each pixel is defined by its coordinate location in the grid, and its color. To draw an object on the screen, you specify which pixels to change, and how to color those pixels. A region only describes the set of pixels to change, and does not describe their color.

The version of regions that you will implement is similar to the regions in the windowing system on the Macintosh. Bill Atkinson developed the first implementation of regions for the Macintosh around 1982. Parts of the code were later patented. Apple has never published the region format, but this has not stopped several large application developers from exploiting the region format. This has kept Apple from changing the region format for 15 years.

Warm up Exercises

Question 1 (5 points)

Create a function called map2 that takes a function f and a pair of lists and applies the function f to corresponding elements of the list, generating a list of the results. That is,

map2 f
([x₁,...,x_n],
[y₁,...,y_n])

should evaluate to

[f(x₁,y₁),...,
f(x_n, y_n)]

. If the lists are of different length, raise the exception WrongLength.

exception WrongLength
val map2 : (('a * 'b) -> 'c ) -> ('a list * 'b list) -> 'c list

Signals

You are going to implement regions using a data structure called a signal. In this section, we will describe what signals are, and how to operate on them, and in the next two sections, we will describe how regions can be viewed as signals.

Suppose you have a sequence of data from a thermometer that is sampled every minute. You can create a naïve encoding of the temperature data by creating a list of time/temperature pairs. Here is a sample of a sequence of winter temperatures starting at 12:00 noon with time encoded as minutes from midnight.

Temp = [(720, 32.0), (721, 32.0), (722, 32.0), (723, 32.0), (724, 32.0), (725,
32.1), (726, 32.1), (727, 32.2), (728, 32.2), ..., (780, 33.0)]

It would be easy to use map to convert this list from Fahrenheit to Celsius. It is also easy to map a function over two lists of temperatures producing a third list. For example, you could make a list of minimum temperatures for each minute of two days by using Real.min with the map2 function. To get the time values to work out, the two temperature lists must start at the same time and end at the same time. Notice many of the temperature readings are the same. The above encoding wastes a lot of space duplicating the same readings for several minutes. We can save space by removing the redundant data from the list and only keeping the transitions to new temperatures and the time of the temperature change. Here is an example of the Temp list with the redundant entries removed.

CompactTemp = [(720, 32.0), (725, 32.1), (727, 32.2), ...]

A map2 function is more complicated than with the naive encoding. Each time/value pair represents the value of the reading until the transition point. For this reason, the result of a function applied to both signals will only change values if there is a transition in one of the two lists. Ensuring the output list doesn't have any redundant entries makes the problem even more difficult. Here is an example of taking the minimum temperature per minute of two days. Assume two sets of data.

Day1 = [(720, 32.0), (725, 32.1), (727, 32.2), ...])
Day2 = [(720, 32.1), (723, 32.0), (726, 31.9), (727, 31.8), (729, 31.7), ...]

Here is the result of taking the minimum temperatures of Day1 and Day2 on a per minute basis.

Result = [(720, 32.0), (726, 31.9), (727, 31.8), (729, 31.7), ...]

A signal generalizes the above ideas. The discussion above used finite lists as to record the temperature data. In general, signals should be infinite in both directions with a finite number of transitions. By pairing transition lists with an initial value, you can represent an infinite series of values. The initial value represents the value of the signal before the first transition. In addition, assume that the signal has the value of the last transition forever after the last transition. The type for a signal is now a pair consisting of an initial value and a list of time/value pairs.

type signal = value * (time * value) list;

A signal must satisfy the following signal invariants:

Ordering: the time indices in the list are strictly increasing from left to right
Irredundancy: the initial value is different from the first value in the list (if such a value exists), and two consecutive values are never the same.

An implementation of signals should satisfy the following signature.

signature SIGNAL =
sig
  type time       (* Parameter, must be ordered *)
  type value      (* Parameter, must admit equality *)

  type signal     (* Abstract *)

  (* You can assume the transition list satisfies the signal invariants. *)
  (* Takes a list and converts it to a signal. *)
  val fromList : value * (time * value) list -> signal

  (* Returns true if the transition list obeys invariants, false otherwise. *)
  val checkList : value * (time * value) list -> bool

  (* Takes a signal and converts it to a list. *)
  val toList : signal -> value * (time * value) list

  (* Maps a function over the values in a signal. *)
  val map : (value -> value) -> signal -> signal

  (* Maps a function over a pair of signals. *)
  val map2 : (value * value -> value) -> signal * signal -> signal

  (* Convert a signal to a function from time to values *)
  val eval : signal -> (time -> value)

  (* Compares two signals. *)
  val equal : (signal * signal) -> bool
end (* signature SIGNAL *)

In the SIGNAL signature, the types time and value are to be thought of as parameters. We use where type to create instances of SIGNAL with concrete types for time and time. For example, a temperature signal has the following declaration.

signature TEMP_SIGNAL = SIGNAL where type time = int
	                       where type value = real;

In order to maintain the signal invariants, the type time must be ordered and type value must admit equality. For this, we use two signatures.

signature ORDER =
sig
  type t  (* parameter *)
  val compare : t * t -> order
end;

signature EQUAL =
sig
  type t  (* parameter *)
  val equal : t * t -> bool
end;

Question 2 (50 points)

Create the following functor which implements a SIGNAL given structures for transitions and values.

functor Signal (structure Time : ORDER
	        structure Value : EQUAL)
  :> SIGNAL where type time = Time.t
            where type value = Value.t

The type signal should be implemented as

type signal = value * (time * value) list

as explained above.

Make sure your functions take advantage of and preserve the signal invariants!

Sets as Signals

Finite and even some infinite sets can be encoded as signals. Recall that the characteristic function of a set returns true given a value in the set and otherwise false. We can use a set's characteristic function to create a boolean signal. Consider, for example, the set S = {10,11,12,13,23,24,25} and its characteristic function F_S. We have, for example, are F_S(3) = false, F_S(11) = true and F_S(100) = false.

The graph of a any function f is the set {(x, f(x)) | x in D} where D is the domain of f. If we take the graph of our example characteristic function F_S we get the set:

{..., (9, false), (10, true), (11, true), (12, true), (13, true), (14, false),
..., (22, false), (23, true), (24, true), (25, true), (26, false), ...}.

We know that the values before 10 are false, and the values after 26 are false, so we can turn this directly into the following boolean signal:

(false, [(10,true), (14, false), (23, true), (26, false)])

Question 3 (20 points)

An implementation of a structure

signature BOOL_SIGNAL = SIGNAL where type time = int 
	                       where type value = bool;
structure BoolSignal :> BOOL_SIGNAL

is provided in the file ass4.sml. The interface for integer sets is given by the following signature.

signature INTSET =
sig
  type intset

  val int : intset  (* set of all integers *)
  val nat : intset  (* set of integers >= 0 *)
  val empty : intset  (* empty set of integers *)
  val union : intset * intset -> intset
  val intersect : intset * intset -> intset
  val difference : intset * intset -> intset

  val member : int * intset -> bool
end;

Write a functor

functor IntSet (structure BS : BOOL_SIGNAL)
  :> INTSET where type intset = BS.signal =
struct
  type intset = BS.signal
  ...
end;

Hint: You should find the function map2 most useful.

Regions as Signals

Regions describe what pixels are going to be affected during a graphics operation. A region is a set of locations of pixels.

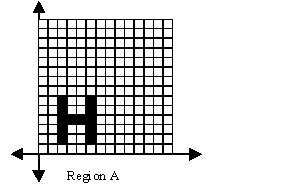
A = {(2,1), (5,1), (2,2), (5,2), (2,3), (3,3), (3,4), (3,5), (2,4), (5,4),  (2,5), (5,5) }

Region operations can be thought of as set operations over sets of pixel locations. For example, if you have the region B = {(2,2),(3,2),(4,2),(5,2)} then the intersection of region A and region B is the set of pixel locations {(2,2),(5,2)}. Representing regions as sets of pixels has a lot of redundant data. To shrink the representation, gather all the pixels for the same row, and removing the y-components from the location pairs and store a single y value with a set of x values. This representation of regions has the form {(Y position, {X set}), ...}. Then take that set and sort it into a list by Y position. The region A in the new format looks like this:

A = [(1, {2,5}), (2, {2,5}), (3, {2,3,4,5}), (4, {2,5}), (5, {2,5})]

Operations for this format are similar to operations in the naive set format. To calculate the intersection of regions A and B, calculate the intersection of the X sets for each of the row pairs in A and B. If the row does not exist, assume its X set is empty. In this format notice that some of the rows have the same X set. We can now convert a region into a signal where Y is the transition time, and the X set is the value. The above region A becomes the signal:

SignalA = ({},[(1,{2,5}),(3,{2,3,4,5}),(4,{2,5}),(6,{})])

Here the empty set at row 6 means that there are no pixels in the set that have a y component greater that 5. The initial set being empty means that there are no values before the first transition at row 1.

Question 4 (5 points)

Implement the structure Region using the structure BoolSignal and the functor Signal satisfying the signature REGION.

signature REGION =
  SIGNAL where type time = int
         where type value = BoolSignal.signal;

Question 5 (10 points)

Implement empty, union, intersect and difference for regions.

val empty : Region.signal
val union : (Region.signal * Region.signal) -> Region.signal
val intersect : (Region.signal * Region.signal) -> Region.signal
val difference : (Region.signal * Region.signal) -> Region.signal

For this, the operations in structure IntSet and Region.map2 should be very helpful.

Question 6 (10 points)

Implement the function fromRectangle which takes two opposite corners of a rectangle, and produces a region. You may not assume the corners are in the proper order.

type rectangle = ((int * int) * (int * int))
val fromRectangle : rectangle -> Region.signal

Question 7 (20 points extra credit)

The function calcVisRgn is the core of the Macintosh windowing system. It takes a list of rectangles, and returns a list of the visible portions of the windows. Rectangles that come first in the list obscure rectangles later in the list.

val calcVisRgn = rectangle list -> Region.signal list;

Handin instructions

Put your SML code into a single file named ass4.sml in your ass4 directory. All of your definitions should be in this one file. Please keep a backup for your records. Your handin directory for this assignment is

/afs/andrew/scs/cs/15-212-X/studentdir/<your andrew id>/ass4/