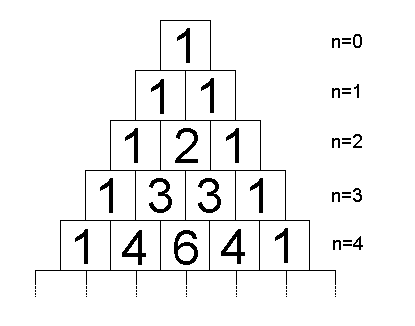
15-212-X : Homework Assignment 1

Due Wed Sep 10, 2:00 pm (electronically); papers at recitation.

Maximum Points: 50 (+10 extra credit)

Guidelines

Strive for elegance! Not every program which runs deserves full credit. Make sure to state invariants in comments which are sometimes implicit in the informal presentation of an exercise. If auxiliary functions are required, describe concisely what they implement. Do not reinvent wheels and try to make your functions small and easy to understand. Use tasteful layout and avoid longwinded and contorted code. None of the problems requires more than a few lines of SML code.
Make sure that your file compiles and runs. A program which doesn't run will not get full credit and is likely to incur a heavy penalty.
Homeworks must be all your own work.
Late homeworks will be accepted only until start lecture on Thursday, with a 25% penalty.
If you have any questions about this assignment, contact Frank Pfenning at fp@cs or use cmu.andrew.academic.15-212-X.discuss.

Problem 1: Binomial numbers (15 pts) (+10 extra credit)

Binomial numbers play an important role in combinatorics because they answer the question of how many subsets can be formed by picking r elements out of a set of n ("n choose r" or "n over r"). There are several ways to calculate binomials. One way is by using factorials, the other one by reading them out of Pascal's triangle. One of the aims of this problem is to show the equivalence between both definitions.

First, the factorial function on natural numbers is defined mathematically as follows:

0!	=	1
n!	=	n * (n-1)!	for n > 0

The factorial function is the basis for the first definition of binomial numbers. BN(n,r) denotes the binomial number for (n,r) or "n choose r". It is defined as follows:

BN(n,r)

n!
---------
r! (n-r)!

for 0 <= r <= n

A way to calculate binomial numbers which does not require factorials is to use Pascal's triangle. The triangle has a 1 at its top, every other number in the Pascal triangle is defined as the sum of the numbers to the right and to the left above. If there isn't any number, it counts as zero.

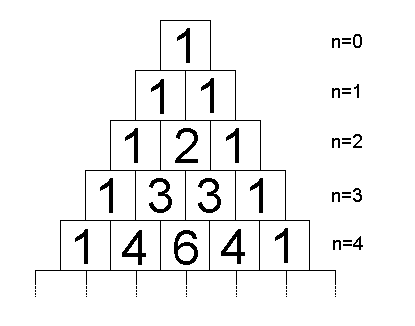
We denote a binomial number defined by the Pascal triangle as PT(n,r), where n stands for the row in the figure above, and r counts from left to right, starting at 0.

Question 1.1 (5 pts)

Write an ML program to calculate PT(n,r). Your function should be named pascal and must have type int * int -> int . Calculate the following values PT(5,3) and PT(7,1) .

Question 1.2 (10 pts)

Show by induction that pascal is a correct implementation of the binomial as defined using factorials. Carefully state and check the boundary conditions! You don't need to type your proof in (writing it by hand and handing it in at recitation is usually faster and easier).

Question 1.3 (extra credit, 10 pts)

Give a straightforward implementation of a function binomial which uses factorials. This implementation is likely to lead to rather frequent overflow exceptions. Test it to find some values of n and r where the computation requires intermediate results which exceed the size allowed by the machine representation of integers. Compare this to the function pascal. Consider how you might define a function to compute binomials based on multiplication which works for a larger set of natural numbers. [Of course, eventually the result will be too large to be representable with machine integers and no further improvement is possible without another implementation of integers.]

Problem 2: Implementing Transcendental Functions (20 pts)

A frequently used technique for computing transcendental functions is the Maclaurin series. It has the form

and approximates the function f near 0.

In the case of the exponential function, we obtain

This can be rewritten as

and implemented by the following function

fun exp3 (0, x, y) = y
  | exp3 (k, x, y) = exp3 (k-1, x, 1.0 + (x / real(k)) * y)

fun exp0 (x:real) = exp3 (13, x, 1.0);

Here, exp0 approximates the exponential function near 0, using the first 13 terms of the Maclaurin series.

Question 2.1 (5 pts)

Prove that exp3(k,x,y) evaluates to

for k > 0.

Question 2.2 (5 pts)

The exp0 function is only accurate near 0. Assume you want to rely on exp0 only for arguments between 0 and 1. Write a function exp : real -> real which is accurate for arbitrary real arguments. You do not need to prove the correctness of this function.

Compare the results of your function with the built-in function Math.exp on a few values.

Question 2.3 (10 pts)

The sine function can be approximated near 0 by the Maclaurin series

Proceed as above:

Factor the series similar to the exponential.
Write an efficient approximation sin3 accurate near 0.
Carefully state and prove its correctness as above.
Using the periodicity of the sine function, write a function sin : real -> real which reduces arbitrary arguments to the interval between 0 and pi/2.
Compare your function to Math.sin on a few values.

Problem 3: Numerical Integration (15 pts)

The second problem treats some computations with real numbers and functions over them. We will discuss and implement a method for numerical integration of functions of one argument. Numerical integration means, that we look for a good approximation of the integral, but not for a "closed form". Naturally, we cannot expect to guess the solution with the first approximation, therefore we must calculate a sequence of approximation values, each an improvement of the previous one. The idea behind this approximation is very simple: Consider the graph of a function

Function Graph

and an equi-distant partition of the x-axis between some points a and b. What happens if we calculate the area of the trapezoids below?

Approximation of Integral

We expect to obtain an approximation value which is close to the integral. It is one of the easier theorems of Calculus that with finer partitions we can hope for a more refined approximation result.

Typically in search for a good approximation value, we continue this kind of splitting in the same fashion. The nth approximation value is hence determined by the sum of 2ⁿ rectangles. Next we must define a criteria for deciding when to stop with the partition refinement. Unfortunately, your program cannot access the "real" value of the integral, so we must define the criteria on the basis of the previous approximation value and the current value. We accept an approximation value if the absolute value of the difference between previous and current value is less then a given (positive) epsilon.

Question 3.1 (10 pts)

Write an SML function
integrate : real -> (real -> real) -> (real * real) -> (int * real)
where integrate epsilon f (a,b) approximates the integral of f between a and b up to epsilon. It returns a a pair, where the first component yields the current refinement level (n, not 2ⁿ), and the second the approximation value, fulfilling the condition from above. Integrate

the sine function between 0 and pi
the exponential function between 0 and 1
the function f(x) = cos(2*pi*sin(x)) between 0 and pi
and check which integral converges fastest for epsilon = 10^-6 (that is, 0.000001).

Hint: Use the context browser to access information about the mathematical functions from the Math structure.

Question 3.2 (5pts)

Now fix epsilon = 10^-6 (= 0.000001) and write a function
integrate0 : (real -> real) -> (real -> real)
where integrate0 f is the function g(x) which represents the value of the integral of f between 0 and x, approximated with bound epsilon.

Handin instructions

Put your SML code into a file named ass1.sml in your ass1 directory. All of your definitions should be in this one file. Your handin directory is

/afs/andrew/scs/cs/15-212-X/studentdir/<your andrew id>/ass<number>

Hand in your proofs for Question 1.2, 1.3, 2.1, 2.3 on paper at the recitation.