15-212-X : Homework Assignment 2

Due Wed Sep 25, 10:00 am (electronically); papers at recitation.

Maximum Points: 100(+20 extra credit)

Guidelines

Problem 1: Warm up (10 pts)

A student distrusting his bank decides to write his own accounting program to keep his day-by-day expenses under control. Since he is a precise person, he wants to keep track of all his coins and of their relative value. For this purpose, he implements the following conversion table.

equals Quarters Dimes Nickels Pennies
1 Quarter 1 2.5 5 25
1 Dime 0.4 1 2 10
1 Nickel 0.2 0.5 1 5
1 Penny 0.04 0.01 0.2 1

Since he is particularly zealous, he makes explicit the arithmetic properties that relate these values. His programming masterpiece results in the following Standard ML declarations.

This program can be accessed directly as the file

Unfortunately, his program contains several errors ...

Question 1.1 (4 pts)

Identify the errors and explain them in your own words.

Question 1.2 (4 pts)

Write a correct version of the above function.

Question 1.3 (2 pts)

Is it really a good idea to make the arithmetic relationships among the different coins as explicit as possible? Why?

Problem 2: Fibonacci Trees (40 pts)

Leonardo da Pisa, son of Bonacci, better known as Fibonacci ("Filius Bonaccii") is nowadays well-known mainly to mathematicians and computer scientists for the sequence of numbers that bear his name:

f0 = 1
f1 = 1
fn+2 = fn+1 + fn

One of his major concerns in life (1180-1250) were however rabbits. In particular, he was interested in knowing how rabbits reproduce and, assuming to start with one male and one female rabbit, how many rabbits he would get after any fixed amount of time. For this purpose, he came up with the following (admittedly approximate) discrete model of rabbit reproduction:

Starting from one couple of young rabbits, the evolution of the rabbit population can be represented by the infinite sequence of Fibonacci trees which first five elements are as follows:

Couples of young rabbits are represented as empty circles, while adults are pictured as squares. Internal nodes contribute to the tree structure and can serve the purpose, for example, of computing the age of the rabbits.

The n-th element of this sequence, that we will denote as Tn, is a snapshot of the rabbit population at month n.

Question 2.1 (10 pts)

Given the following declaration describing the structure of Fibonacci trees

write an SML function nextFibTree, of type fibTree -> fibTree, that, given an object of type fibTree, expands its leaves according to Fibonacci's specification of rabbit reproduction, as exemplified in the figure above.

Use nextFibTree to write a function createFibTree of type int -> fibTree that, given a natural number n, generates Tn (raise the exception General.Domain if you are given a negative input argument).

Question 2.2 (15 pts)

Prove that, for any natural number n, Tn+2 is a binary tree having Tn as its left subtree and Tn+1 as its right subtree, i.e., show that

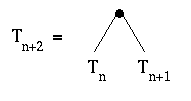On the basis of this property and of examples shown in class, devise an efficient implementation of the function createFibTree' performing the same task as the function createFibTree from the previous question. Prove its correctness.

Question 2.3 (15 pts)

Write an SML function countFibTreeLeaves, of type fibTree -> int, that returns the total number of leaves of the Fibonacci tree Tn passed to it as an argument. Notice that this is the number of rabbit couples in the n-th month.

Prove the following mathematical property about Fibonacci trees:

Question 2.4 (Extra credit: 10 pts)

Modify the above idealistic situation so that rabbits are cooked and eaten when they reach a certain age. Describe the shape of the consequent variant of Fibonacci trees and the evolution of the population of (still alive) rabbits in the case this tragic ending is fixed when they are 2 months old. What if it happens when they are 3 months old? For ethical reasons, always assume the genocide to take place after the birth of the young rabbits.

Problem 3: Sets, Relations, Graphs, and Airplanes (50 pts)

Sets play an important role as the foundation of most areas in Mathematics. Mathematicians enjoy working with extremely large sets, far beyond infinity. Sets are also a useful form of abstraction in Computer Science, although they are seldom used in practice due to their high manipulation overhead. Ways to implement certain countable (i.e. mildly infinite) collections of data will be described further on in the course. In this exercise, we will instead concentrate on finite sets, related concepts (relations and graphs), and their use in a small application.

Question 3.1: Finite Sets (10 pts)

We consider a simple implementation of the set data structure based on the list type of SML. The following declaration serves this purpose:

Lists can be exploited in different manners as a support to the representation of sets. The choice is left entirely to you: what matters is that the functions you are requested to implement manifest their expected behavior.

Give a correct implementation of a structure, that you will call Set, that satisfies the following signature (accessible in the file sets.sig in this assignment's directory)

signature SET =
sig

  type 'a set = 'a list
  exception Set

  val emptySet : ''a set
  val setInsert : ''a * ''a set -> ''a set
  val setRemove : ''a * ''a set -> ''a set
  val isSetEmpty : ''a set -> bool
  val setMember : ''a * ''a set -> bool
  val setToList : ''a set -> ''a list
  val listToSet : ''a list -> ''a set

  val setUnion : ''a set * ''a set -> ''a set
  val setIntersection : ''a set * ''a set -> ''a set
  val setDifference : ''a set * ''a set -> ''a set
end;

and the specifications below for the values it mentions

Question 3.2: Relations (10 pts)

A binary relation is a set having ordered pairs of objects as its elements. The set of objects that are allowed as the first components of these pairs form the domain of the relation. Similarly, the elements that can appear as the second component of the pairs form its codomain.

On the basis of this definition, the representation of relations is immediate:

Use the operations contained in the structure Set you just wrote in order to define the structure Rel implementing some basic operations on relations, as specified by the following signature (file rel.sig in this assignment's directory):

signature RELATION =
sig

  type ('a, 'b) relation = ('a * 'b) Set.set

  val relImage : ''a * (''a, ''b) relation -> ''b Set.set
  val relCoimage : ''b * (''a, ''b) relation -> ''a Set.set
  val relJoin : (''a, ''b) relation * (''b, ''c) relation -> (''a, ''c) relation
  val relInverse : (''a, ''b) relation -> (''b, ''a) relation
end;

These operations ought to realize the following functionalities:

Question 3.3: Graphs (5 pts)

In its most basic form, a graph is a relation having identical domain and codomain. Therefore, the following declaration suffices to capture these entities:

Each pair (x,y) in a graph has a natural graphical interpretation as a directed edge from x to y, seen as nodes under this perspective. A node y is reachable from a node x if there is a sequence of edges that lead from x to y. This sequence is called a path from x to y. A traversal of a graph is a method that visits all the nodes that are reachable from a given node. We will consider a specific traversal method, known as depth-first.

We have the following signature for graphs

signature GRAPH =
sig

 type 'a graph = ('a, 'a) Rel.relation

  val depthFirst : ''a * ''a graph -> ''a Set.set
end;

and the following structure realizing it:

structure Graph :> GRAPH =
struct

  type 'a graph = ('a, 'a) Rel.relation

  (* val depthFirst : ''a * ''a graph -> ''a Set.set *)
  fun depthFirst (x, g)=
    let
      (* val df' : ''a list * ''a Set.set -> ''a Set.set *)
       fun df' (nil, visited) = visited
         | df' (x::xs, visited) =
            if Set.setMember (x, visited)
               then df' (xs, visited)
               else
                 let
                   val vs = Rel.relImage (x, g)
                 in
                   df' ((Set.setToList vs) @ xs, Set.setInsert (x, visited))
                 end
    in
      df' ([x], Set.emptySet)
    end
end;

both can be found in the file graph.sml in the assignment's directory.

Fill in the documentation for the function depthFirst. Give an informal but convincing description of how it traverses a connected subgraph. You should cover correctness and termination: although we do not expect a formal proof, the reader of your solution should have a clear understanding of how the function uses recursion to solve the problem.

Question 3.4: Airplane Flight Planning (25 pts)

We are going to use sets, relations and graphs to do some very simple airplane flight planning. We are given a list of cities together with their geographical coordinates. We have an airplane and would like to fly from one city to another. However, the plane can fly only a limited distance without landing and refueling; this distance is shorter than the distance to our destination. Therefore, we would like to come up with a flight plan such that each city-to-city hop is short enough and allows us to eventually reach our destination.

Your job is to implement a program that will give us the information we need to decide on a flight plan. In order to help you along, we have written a series of functions you can use to manipulate longitude/latitude coordinates.

The interface of these functions is specified by the following signature, available in the file air-distance.sml in the assignment's directory:

signature AIRDIST =
sig

  eqtype coord

  val toCoord : real * real -> coord
  val long : coord -> real
  val lat  : coord -> real
  val airDistance : coord * coord -> real
end;

where

These functions are declared in the structure AirDist, implemented in the same file, that you will use to access them. You are not expected to implement this structure: we already did it for you.

You will be requested, among other things, to provide a structure, FlightPlanning, implementing the following signature (file flightPlan.sig in the assignment's directory).

signature FLIGHTPLANNING =
sig

  val cities : (string, AirDist.coord) relation
  val neighbors : string * real * (string, AirDist.coord) Rel.relation
                  -> string Graph.graph
  val allNeighbors : real * (string, AirDist.coord) Rel.relation
                     -> string Graph.graph
  val directFlights : string Graph.graph

  val allPaths : string * string * string Graph.graph -> string list list
  val pathDistance : string list * (string, AirDist.coord) Rel.relation -> real
  val shortestPath : string * string * (string, AirDist.coord) Rel.relation *
                     string Graph.graph -> (string list * real)
  val shortestPath' : string * string * (string, AirDist.coord) Rel.relation *
                      string Graph.graph -> (string list * real)
end;

The expected functionality of the declarations contained in FLIGHTPLANNING are specified in the questions below.

A. Playing with the data (3 pts)

The file

contains some geographic data about major U.S. cities with airports. It is in the following format:

Your first job is to store these data into a relation

Give an expression for determining the distance between Pittsburgh and San Francisco by looking up the two cities in your relation and calling airDistance. What is this distance?

B. Maximum range - calculating one-hop flights (10 pts)

Our next task is to determine all cities that are within flying distance of each other and to construct a graph of those edges.

Define a function, neighbors, that, given a city and the maximum flying distance, returns a (degenerated) graph with edges from the city to all other cities within flying distance from it. The graph should not contain an edge from the city to itself. The type of neighbors is:

Define another function, allNeighbors, that computes the graph af all cities that are within flying distance of each other. Notice that this graph is symmetric: if (a,b) is in it, it contains (b,a) as well. The type of allNeighbors is:

Compute the graph of all city pairs which are within 1000 Km from each other. Call this graph directFlights.

How many cities are within 1000 Km from Wilmington? Which are they?

C. All paths between two cities (12 pts)

Write a function, allPaths, that computes all loop-free paths between two cities. A path in a graph is loop-free if it does not pass twice by the same vertex. The type of this function should be

Hint: Your function is likely to share similarities with depthFirst from question 3.3.

How many paths are there from Eugene to Boston?

Write a function, pathDistance, to compute the total distance travelled on a path:

Write a function, shortestPath, to compute the shortest path from one city to another. There are much more efficient methods, but for this assignment, we only require the slow, brute-force approach using allPaths and pathDistance. The type of the function will be:

What is the shortest path from Eugene to Boston?

D. Optimizing the shortest path (extra credit: 10 pts)

Write a function, shortestPath', which directly computes the shortest path from one city to another without necessarily generating all paths between the cities first.

Handin instructions