Data Mining Assignment 3: Sample Input

Problem 2

Sample Files:

Test files

Coins:

We need to determine which coins are valuable for collectors, and we view valuable coins as positive examples; the training set includes six examples:
 
Class Rarity Age Wear
positive rare new low
positive rare old low
positive common old low
negative rare old high
negative common new low
negative common new high

We compute the information gain of each attribute:
 
Gain(Rarity) = I(3/6, 3/6) - (3/6) * I(2/3, 1/3) - (3/6) * I(1/3, 2/3) = 0.082
Gain(Age) = I(3/6, 3/6) - (3/6) * I(2/3, 1/3) - (3/6) * I(1/3, 2/3) = 0.082
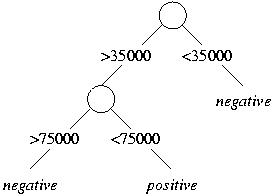
Gain(Wear) = I(3/6, 3/6) - (4/6) * I(3/4, 1/4) - (2/6) * I(0,1) = 0.459

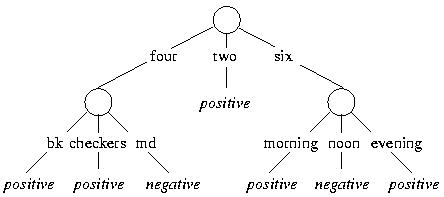
The "wear" attribute provides the greatest gain, and we use it for the root split:

All training examples with high wear are negative; since both test instances have high wear, they are also classified as negative:
 
Rarity Age Wear Class
rare new high negative
common old high negative

The coins with low wear require an additional split, but this split does not affect the classification of the given test instances.

Books:

We next learn to distinguish between cheap and expensive books, and we consider expensive books as positive examples. The training set includes eight books described by five attributes:
 
Class Bind Style Pictures Popularity Length
positive hardcover novel nocolor popular long
positive softcover textbook nocolor popular long
negative softcover novel nocolor popular short
positive hardcover textbook color popular short
positive hardcover journal color unknown short
negative softcover textbook nocolor unknown short
positive hardcover journal color popular long
negative softcover novel color unknown short

We first determine the information gain of each attribute:
 
Gain(Bind) = I(3/8, 5/8) - (4/8) * I(1, 0) - (4/8) * I(3/4, 1/4) = 0.549
Gain(Style) = I(3/8, 5/8) - (3/8) * I(1/3, 2/3) - (3/8) * I(2/3, 1/3) - (2/8) * I(1, 0) = 0.266
Gain(Pictures) = I(3/8, 5/8) - (4/8) * I(2/4, 2/4) - (4/8) * I(3/4, 1/4) = 0.049
Gain(Popularity) = I(3/8, 5/8) - (5/8) * I(4/5, 1/5) - (3/8) * I(1/3, 2/3) = 0.159
Gain(Length) = I(3/8, 5/8) - (3/8) * I(1, 0) - (5/8) * I(2/5, 3/5) = 0.348

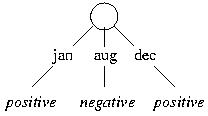
The "bind" attribute gives the greatest gain, and we use it for the root split. All training examples with "hardcover" are positive, whereas the "softcover" examples require an additional split:

We show the "softcover" examples in the following table.
 
Class Bind Style Pictures Popularity Length
positive softcover textbook nocolor popular long
negative softcover novel nocolor popular short
negative softcover textbook nocolor unknown short
negative softcover novel color unknown short

We next compute the information gains of the remaining attributes for the "softcover" examples:
 
Gain(Style) = I(1/4, 3/4) - (2/4) * I(1/2, 1/2) - (2/4) * I(0, 1) = 0.311
Gain(Pictures) = I(1/4, 3/4) - (3/4) * I(2/3, 1/3) - (1/4) * I(0, 1) = 0.123
Gain(Popularity) = I(1/4, 3/4) - (2/4) * I(1/2, 1/2) - (2/4) * I(0, 1) = 0.311
Gain(Length) = I(1/4, 3/4) - (1/4) * I(1, 0) - (3/4) * I(0, 1) = 0.811

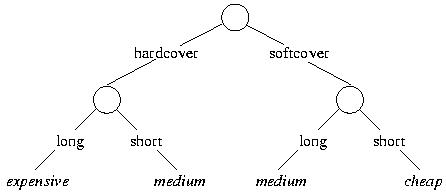
The "length" attribute provides the greatest gain, and we use it for the next split. The resulting tree shows that hardcover books and long softcover books are expensive, whereas short softcover books are cheap:

This tree leads to the following classification of the test instances:
 
Bind Style Pictures Popularity Length Class
softcover journal color popular short negative
softcover novel nocolor unknown long positive
hardcover textbook nocolor unknown short positive

Days

The task is to distinguish Sunday from Monday; Sunday is positive, and Monday is negative.

Weather

The attributes are a state, month, and city, and the task is to determine whether a traveler needs a sweater when visiting this city.

Food

We need to decide whether to buy a hamburger; the attributes include the dollar cost of the hamburger, place (Checkers, Burger King, or McDonald's), and time.

Problem 3

Sample Files:

Test files

Multiple classes:

We consider the classification of books into three price categories: cheap, medium, and expensive.
 
Class   Bind   Style   Pictures   Popularity   Length
expensive   hardcover   novel   nocolor   popular   long
medium   softcover   textbook   nocolor   popular   long
cheap   softcover   novel   nocolor   popular   short
medium   hardcover   textbook   color   popular   short
medium   hardcover   journal   color   unknown   short
cheap   softcover   textbook   nocolor   unknown   short
expensive   hardcover   journal   color   popular   long
cheap   softcover   novel   color   unknown   short

The information gains of the attributes are as follows:
 
Gain(Bind) = I(2/8, 3/8, 3/8) - (4/8) * I(2/4, 2/4, 0) - (4/8) * I(0, 1/4, 3/4) = 0.656
Gain(Style) = I(2/8, 3/8, 3/8) - (3/8) * I(1/3, 0, 2/3) - (3/8) * I(0, 2/3, 1/3) - (2/8) * I(1/2, 1/2, 0) = 0.622
Gain(Pictures) = I(2/8, 3/8, 3/8) - (4/8) * I(1/4, 1/4, 2/4) - (4/8) * I(1/4, 2/4, 1/4) = 0.061
Gain(Popularity) = I(2/8, 3/8, 3/8) - (5/8) * I(2/5, 2/5, 1/5) - (3/8) * I(0, 1/3, 2/3) = 0.266
Gain(Length) = I(2/8, 3/8, 3/8) - (3/8) * I(2/3, 1/3, 0) - (5/8) * I(0, 2/5, 3/5) = 0.610

The "bind" attribute gives the greatest gain, which leads to the following split:
 

We next consider the hardcover books, which require an additional split; the set of training examples with "hardcover" is as follows:
 
Class   Bind   Style   Pictures   Popularity   Length
expensive   hardcover   novel   nocolor   popular   long
medium   hardcover   textbook   color   popular   short
medium   hardcover   journal   color   unknown   short
expensive   hardcover   journal   color   popular   long

The computation of information gains shows that "length" is the most informative attribute:
 
Gain(Style) = I(1/2, 1/2, 0) - (1/4) * I(1, 0, 0) - (1/4) * I(0, 1, 0) - (2/4) * I(1/2, 1/2, 0) = 0.500
Gain(Pictures) = I(1/2, 1/2, 0) - (1/4) * I(1, 0, 0) - (3/4) * I(1/3, 2/3, 0) = 0.311
Gain(Popularity) = I(1/2, 1/2, 0) - (3/4) * I(2/3, 1/3, 0) - (1/4) * I(0, 1, 0) = 0.311
Gain(Length) = I(1/2, 1/2, 0) - (2/4) * I(1, 0, 0) - (2/4) * I(0, 1, 0) = 1.000

We thus split hardcover books by "length":

We next consider the set of softcover books in the training set:
 
Class   Bind   Style   Pictures   Popularity   Length
medium   softcover   textbook   nocolor   popular   long
cheap   softcover   novel   nocolor   popular   short
cheap   softcover   textbook   nocolor   unknown   short
cheap   softcover   novel   color   unknown   short

 
The most informative attribute of this set is also "length":
 
Gain(Style) = I(0, 1/4, 3/4) - (2/4) * I(0, 1/2, 1/2) - (2/4) * I(0, 0, 1) = 0.311
Gain(Pictures) = I(0, 1/4, 3/4) - (3/4) * I(0, 1/3, 2/3) - (1/4) * I(0, 0, 1) = 0.123
Gain(Popularity) = I(0, 1/4, 3/4) - (2/4) * I(0, 1/2, 1/2) - (2/4) * I(0, 0, 1) = 0.311
Gain(Length) = I(0, 1/4, 3/4) - (1/4) * I(0, 1, 0) - (3/4) * I(0, 0, 1) = 0.811


We split the softcover books by "length," which gives the final tree:
 

 
We now use this tree to classify the test instances:
Bind   Style   Pictures   Popularity   Length   Class
hardcover novel nocolor unknown long expensive
hardcover   journal   color   popular   short   medium
softcover   textbook   color   popular   long   medium
softcover   novel   nocolor   unknown   short   cheap

Numeric Attributes:

We again consider the problem of identifying valuable coins, and we view valuable coins as positive examples. We now represent wear as a number between 0 and 100%. The training set includes six examples:
 
Class
 
Rarity
 
Age
 
Wear
positive
 
rare
 
new
 
5%
positive
 
rare
 
old
 
10%
positive
 
common
 
old
 
4%
negative
 
rare
 
old
 
20%
negative
 
common
 
new
 
2%
negative
 
common
 
new
 
25%

The candidate thresholds for the "wear" attribute are 3% and 15%; thus, we replace this attribute with two Boolean attributes: "Wear > 3" and "Wear > 15":
 
Class
 
Rarity
 
Age
 
Wear > 3
 Wear > 15
positive
 
rare
 
new
 
yes
 no
positive
 
rare
 
old
 
yes
 no
positive
 
common
 
old
 
yes
 no
negative
 
rare
 
old
 
yes
 yes
negative
 
common
 
new
 
no
 no
negative
 
common
 
new
 
yes
 yes

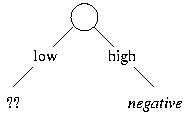
We compute the information gains of these four attributes:
 
Gain(Rarity) = I(3/6, 3/6) - (3/6) * I(2/3, 1/3) - (3/6) * I(1/3, 2/3) = 0.082
Gain(Age) = I(3/6, 3/6) - (3/6) * I(1/3, 2/3) - (3/6) * I(2/3, 1/3) = 0.082
Gain(Wear > 3) = I(3/6, 3/6) - (5/6) * I(3/5, 2/5) - (1/6) * I(0, 1) = 0.191
Gain(Wear > 15) = I(3/6, 3/6) - (4/6) * I(3/4, 1/4) - (2/6) * I(0,1) = 0.459

The most informative attribute is "Wear > 15," which leads to the following split:

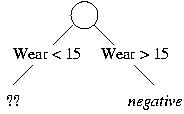
We next consider the training examples with "wear" below 15%:
 
Class
 
Rarity
 
Age
 
Wear > 3
 Wear > 15
positive
 
rare
 
new
 
yes
 no
positive
 
rare
 
old
 
yes
 no
positive
 
common
 
old
 
yes
 no
negative
 
common
 
new
 
no
 no

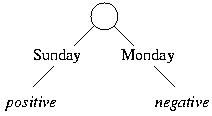
The information gains for the remaining three attributes are as follows:
 
Gain(Rarity) = I(3/4, 1/4) - (2/4) * I(1, 0) - (2/4) * I(1/2, 1/2) = 0.311
Gain(Age) = I(3/4, 1/4) - (2/4) * I(1/2, 1/2) - (2/4) * I(1, 0) = 0.311
Gain(Wear > 3) = I(3/4, 1/4) - (3/4) * I(1, 0) - (1/4) * I(0, 1) = 0.811

The "wear" attribute is again the most informative, which leads to the following tree:

We use this tree to classify the test instances:
 
Rarity Age Wear Class
rare new 20 negative
common old 10 positive
common new 1 negative

Missing Values:

We consider the problem of identifying valuable books, and we use a training set with two missing values:
Class   Bind   Style   Pictures   Popularity   Length
positive   hardcover   novel   nocolor   popular   long
positive   softcover   textbook   nocolor   popular   long
negative   softcover   novel   nocolor   popular   MISSING
positive   hardcover   textbook   color   MISSING   short
positive   hardcover   journal   color   unknown   short
negative   softcover   textbook   nocolor   unknown   short
positive   hardcover   journal   color   popular   long
negative   softcover   novel   color   unknown   short

We observe that the majority of positive examples are "popular," and the majority of negative examples are "short," which leads to the following "repair" of the missing values:
 
Class   Bind   Style   Pictures   Popularity   Length
positive   hardcover   novel   nocolor   popular   long
positive   softcover   textbook   nocolor   popular   long
negative   softcover   novel   nocolor   popular   SHORT
positive   hardcover   textbook   color   POPULAR   short
positive   hardcover   journal   color   unknown   short
negative   softcover   textbook   nocolor   unknown   short
positive   hardcover   journal   color   popular   long
negative   softcover   novel   color   unknown   short

The information gains for these repaired examples are as follows:
 
Gain(Bind) = I(3/8, 5/8) - (4/8) * I(1, 0) - (4/8) * I(3/4, 1/4) = 0.549
Gain(Style) = I(3/8, 5/8) - (3/8) * I(1/3, 2/3) - (3/8) * I(2/3, 1/3) - (2/8) * I(1, 0) = 0.266
Gain(Pictures) = I(3/8, 5/8) - (4/8) * I(2/4, 2/4) - (4/8) * I(3/4, 1/4) = 0.049
Gain(Popularity) = I(3/8, 5/8) - (5/8) * I(4/5, 1/5) - (3/8) * I(1/3, 2/3) = 0.159
Gain(Length) = I(3/8, 5/8) - (3/8) * I(1, 0) - (5/8) * I(2/5, 3/5) = 0.348

The "bind" attribute provides the greatest gain, which leads to the following split:

We next consider the softcover books, which require an additional split:
 
Class Bind Style Pictures Popularity Length
positive softcover textbook nocolor popular long
negative softcover novel nocolor popular MISSING
negative softcover textbook nocolor unknown short
negative softcover novel color unknown short

The majority of negative examples in this table are short books, which means that we again replace the missing value with "short":
 
Class Bind Style Pictures Popularity Length
positive softcover textbook nocolor popular long
negative softcover novel nocolor popular SHORT
negative softcover textbook nocolor unknown short
negative softcover novel color unknown short

We compute the information gain of the remaining four attributes:
 
Gain(Style) = I(1/4, 3/4) - (2/4) * I(1/2, 1/2) - (2/4) * I(0, 1) = 0.311
Gain(Pictures) = I(1/4, 3/4) - (3/4) * I(2/3, 1/3) - (1/4) * I(0, 1) = 0.123
Gain(Popularity) = I(1/4, 3/4) - (2/4) * I(1/2, 1/2) - (2/4) * I(0, 1) = 0.311
Gain(Length) = I(1/4, 3/4) - (1/4) * I(1, 0) - (3/4) * I(0, 1) = 0.811

The "length" attribute is the most informative, which leads to the following tree:

This tree is identical to the tree in Problem 2, and we get the same classification of the test instances:
 
Bind Style Pictures Popularity Length Class
softcover journal color popular short negative
hardcover novel nocolor unknown long positive
softcover textbook nocolor unknown long positive

Gasoline

The task is to select an appropriate gasoline type, which may depend on the vehicle type (sports, SUV, or economy), engine compression (low, medium, or high), and income of the driver (poor or rich).

Loans

We need to approve or disapprove a loan application; the attributes include the income of an applicant, graduate education ("yes" if she has a graduate degree), and home ownership ("yes" if she owns her home).

Medicine

We need to determine whether a patient needs a new medication based on four symptoms: fever, blood pressure (low, medium, or high), headache (yes or no), and allergy.

Back to the Data Mining home page