Exploring Tekkotsu Programming on Mobile Robots

Exploring Tekkotsu Programming on Mobile Robots:

Shape Primitives

Contents: Types of shapes, Vectors of shapes, Extracting line shapes, Describing endpoints, Mixing sketch and shape operations, Constructing new lines, Ellipses, Assignment and copying, Exercises, Data structures

Types of Shapes

In the introductory section on VisualRoutinesBehavior we saw an example of extracting blob shapes from a Sketch<uchar>. Following the convention we established for sketches, we'll use the lowercase term "shape" to refer to actual shapes, and the capitalized term Shape to refer to a smart pointer to one of those shapes. Blobs are described by BlobData objects, and smart pointers to blobs are called Shape<BlobData>. Blobs are one of several types of shapes supported by Tekkotsu. Their names all end in "Data", and they are all children of the BaseData class. Here is a list:

Basic shapes: PointData, LineData, EllipseData

Complex shapes: PolygonData, BlobData, MarkerData

3-D shapes: SphereData, BrickData

Robot shape: AgentData (robot position and orientation on the world map)

Extracted shapes live in a ShapeSpace, which is the dual of the SketchSpace they came from. For the camera sketch space camSkS, the dual space is called camShS.

Vectors of Shapes

Let's revisit the code for extracting blob shapes from a sketch. Shape extraction operators generally return vectors of shapes. The NEW_SHAPEVEC macro is a bit of syntactic sugar to bind a variable to the result. And SHAPEVEC_ITERATE sets up an iteration to provide for convenient processing of the vector.

#include "Behaviors/StateMachine.h"
using namespace DualCoding;

$nodeclass DstBehavior : VisualRoutinesStateNode : doStart {
  NEW_SKETCH(camFrame, uchar, sketchFromSeg());
  NEW_SKETCH(orange_stuff, bool, visops::colormask(camFrame,"orange"));
  NEW_SHAPEVEC(blob_shapes, BlobData, BlobData::extractBlobs(camFrame,100));
  NEW_SKETCH(blob0, bool, 
    blob_shapes.size() > 0 ? blob_shapes[0]->getRendering()
                           : visops::zeros(camFrame));
  SHAPEVEC_ITERATE(blob_shapes, BlobData, myblob)
    cout << "Id: " << myblob->getId()
         << "  Color: " << myblob->getColor()
         << "  Area: " << myblob->getArea()
         << endl;
  END_ITERATE;
}

Below are the extracted blobs. This display was produced by clicking on "Select All Shapes" in the CamSpace window, and clicking the "ID" checkbox in the CamImg window. The ID numbers displayed in that window are the blob shape IDs, and correspond to the numbers in the GUI display. The blob0 sketch was also selected, and its color inverted (via a right mouse click); this is the rendering of the extracted blob shape. It's close to the original sketch, but with a small amount of noise removal due to the run length encoding method use to encode the blob.

The output produced by the program is:

Id: 10001  Color: [245,113,65]  Area: 1968
Id: 10002  Color: [245,113,65]  Area: 1176
Id: 10003  Color: [245,113,65]  Area: 129
Id: 10004  Color: [186,167,12]  Area: 1316
Id: 10005  Color: [186,167,12]  Area: 990
Id: 10006  Color: [186,167,12]  Area: 631

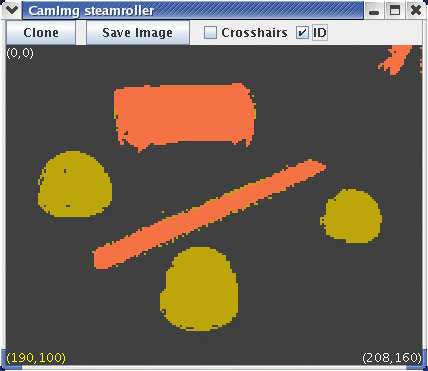
Note that within each color class, the blobs with the greatest area are extracted first. This does not necessaily mean the largest bounding box. For example, the diagonal orange line 10002 has a larger bounding box area than the cylinder, but the latter has more pixels, and is therefore extracted first.

Extracting Line Shapes

Each instance of the LineData class has two endpoints. If both are marked as active, we have a line segment; if only one is active, we have a ray; if neither is active, the we have a true (infinite) line. When lines are extracted from a sketch, if the line runs to the edge of the sketch, that endpoint is marked as invalid and inactive. Otherwise the endpoint is valid and active, but valid endpoints can be made temporarily inactive to extend the line to infinity. Lines also have some derived properties which are recomputed automatically whenever an endpoint moves:

Length Distance between endpoints; ignores valid/active flags.

Orientation Since lines are symmetric, orientations range between 0 and pi. The slope is the tangent of the orientation.

Normal vector (rho,theta) This is the endpoint of a vector from the origin that intersects the line at a right angle. It is expressed as a distance rho (always positive) and an angle theta (0 to 2 pi).

We don't normally work with LineData objects directly. Instead we use the smart pointer Shape<LineData>. Smart pointers provide reference counting and validity checking. Shape<LineData> overloads the -> operator so that successfully dereferencing it gives you access to the LineData's member functions.

The line extraction functions return a vector<Shape<LineData> >. (Note that the space between the two greater-than signs is required for C++ to properly parse the expression.) There are currently two line extraction methods available: one based on moments, and one using the Hough transform.

$nodeclass DstBehavior : VisualRoutinesBehavior : doStart { 
  NEW_SKETCH(camFrame, uchar, sketchFromSeg());
  NEW_SKETCH(pink_stuff, bool, visops::colormask(camFrame,"pink"));
  NEW_SHAPEVEC(lines, LineData, LineData::extractLines(pink_stuff));
}

Active endpoints are indicated in the SketchGUI by a short perpendicular line at the tip of the line segment. Notice that where a line runs out of the camera frame, the endpoint is invalid and hence inactive (no perpendicular line).

Describing EndPoints

The two endpoints of a line are end1Pt and end2Pt. The assignment is arbitrary; there is no guarantee that end1Pt will be the leftmost or topmost of the two. However, when comparing two lines, it is often useful to be able to refer to the left and right endpoints, e.g., two lines might be defined as "close" if their first endpoints are close to each other, and their second endpoints are also close to each other. We can equate first with leftmost and second with rightmost under most circumstances, but if the lines are very close to vertical, and considering that line extraction is subject to noise, our attempt at establishing a correspondence between the two pairs of endpoints might fail. But for near-vertical lines we can safely use top and bottom to designate first and second endpoints. The LineData class provides a set of logical accessors for endpoints that handle these details:

leftPt(), rightPt() leftPt() returns the leftmost of the two endpoints based on their X coordinates; rightPt() returns the rightmost. If the line is vertical the choice is arbitrary, but the two functions will always return different endpoints.

topPt(), bottomPt() topPt() returns the topmost of the two endpoints based on their Y coordinates (smaller values = topmost); bottomPt() returns the botommost. If the line is horizontal the choice is arbitrary, but the two functions will always return different endpoints.

leftPtShape(), rightPtShape(), topPtShape(), bottomPtShape() These functions return a Shape<PointData> instead of a raw EndPoint. The parent is set to the line object.

isHorizontal(),
isVertical() A line is considered to be horizontal if its slope is no greater than 60 degrees; it is vertical if its slope is no less than 30 degrees. Diagonal lines (slopes between 30 and 60 degrees) satisfy both predicates.

firstPt(), secondPt() If the line satisfies isHorizontal(), its first point is the leftmost endpoint. Otherwise its first point is the topmost endpoint. The second point is defined similarly.

firstPtShape(), secondPtShape() Returns the first or second point as a Shape<PointData> rather than a raw EndPoint.

firstPt(otherline), secondPt(otherline) These functions are useful when comparing two lines that might be just on the cusp of satisfying the horizontal test; hence one could pass the test while the other fails. To enforce agreement, we use one line to make the horizontal/vertical decision for both. If otherline satisfies isHorizontal(), this line's first point is the leftmost endpoint; otherwise this line's first point is the topmost endpoint. The second point is defined similarly.

Here is an example of marking the leftmost point of a line. We use a Shape<PointData> to represent the point.

$nodeclass DstBehavior : VisualRoutinesBehavior : doStart {
  NEW_SKETCH(camFrame, uchar, sketchFromSeg());
  NEW_SKETCH(orange_stuff, bool, visops::colormask(camFrame,"orange"));
  NEW_SHAPE(line, LineData, LineData::extractLine(orange_stuff));
  NEW_SHAPE(leftpt, PointData, line->leftPtShape());
  leftpt->setColor("green");
}

Below is the result of our code to label the leftmost point of the line. We've inverted the orange_stuff sketch so we can superimpose the line on top of it.

Mixing sketch and shape operations

The real power of dual coding representations becomes evident when we mix sketch and shape operations together. Consider the problem of determining which side of an orange line has more yellow blobs. The line could be just a line segment, meaning it does not extend across the entire image; this poses no problem for humans, who can still interpret the line as a boundary. To parse such a scene using visual routines, we take the following approach:

Find an orange line shape.
Use visops::topHalfPlane(line) to mark all pixels above the line.
Extract the yellow blobs on each side of the line into separate vectors. Reject any blobs smaller than the minimum size we specify (50 pixels), as those regions are probably noise.
Count the blobs in each vector.
Use a logical-Or operation to combine the renderings of the blobs on the more numerous side, and label this as the result of our computation.
Deactivate the line's endpoints so it extends to infinity when we view it in the SketchGUI.

$nodeclass DstBehavior : VisualRoutinesBehavior : doStart { 
  NEW_SKETCH(camFrame, uchar, sketchFromSeg());
  NEW_SKETCH(orange_stuff, bool, visops::colormask(camFrame,"orange"));
  NEW_SKETCH(yellow_stuff, bool, visops::colormask(camFrame,"yellow"));
  NEW_SHAPE(line, LineData, LineData::extractLine(orange_stuff));
  NEW_SKETCH(topside, bool, visops::topHalfPlane(line));
  NEW_SKETCH(side1, bool, yellow_stuff & topside);
  NEW_SKETCH(side2, bool, yellow_stuff & !topside);
  NEW_SHAPEVEC(side1blobs, BlobData, BlobData::extractBlobs(side1,50));
  NEW_SHAPEVEC(side2blobs, BlobData, BlobData::extractBlobs(side2,50));
  vector<Shape<BlobData> > &winners =
    side1blobs.size() > side2blobs.size() ? side1blobs : side2blobs;
  NEW_SKETCH(result, bool, visops::zeros(yellow_stuff));
  SHAPEVEC_ITERATE(winners, BlobData, b)
    result |= b->getRendering();
  END_ITERATE;
  line->setInfinite();    // for display purposes
}

Constructing New Lines

We can make new lines using the LineData constructor, whose first argumnet is a ShapeSpace. We'll use camShS. Since we want to use smart pointers to manage our shapes, the LineData object should immediately be passed to a shape constructor. In the construction of line2 below, NEW_SHAPE does this automatically for us.

Here is an example of constructing a line by specifying a point the line should pass through, plus an orientation. We can use this form of the LineData constructor to make a line perpendicular to the endpoint of another line.

$nodeclass DstBehavior : VisualRoutinesBehavior : doStart {
  NEW_SKETCH(camFrame, uchar, sketchFromSeg());
  NEW_SKETCH(orange_stuff, bool, visops::colormask(camFrame,"orange"));
  NEW_SHAPE(line1, LineData, LineData::extractLine(orange_stuff));
  line1->leftPt().setActive(false);
  NEW_SHAPE(line2, LineData, new LineData(camShS,line1->rightPt(),line1->getThetaNorm()));
  NEW_SKETCH(corner, bool, visops::seedfill(line1->getRendering() | line2->getRendering(), 0));
  corner->setColor("green");
}

Notice that line2 appears as a child of the root object in the SketchGUI. If we wanted it to appear as a child of line1, we could set its parentId to line1's ViewableId.

Ellipses

Shape<EllipseData> can be used to describe circular or elliptical shapes. This differs from blobs in that the EllipseData::extractEllipses function will reject regions that are not roughly elliptical. Also, EllipseData calculates semimajor and semiminor axis lengths, and the axis orientation, which only makes sense for ellipses.

$nodeclass DstBehavior : VisualRoutinesBehavior : doStart {
  NEW_SKETCH(camFrame, uchar, sketchFromSeg());
  NEW_SKETCH(orange_stuff, bool, visops::colormask(camFrame,"orange"));
  NEW_SKETCH(yellow_stuff, bool, visops::colormask(camFrame,"yellow"));
  NEW_SHAPEVEC(ellipses, EllipseData, EllipseData::extractEllipses(yellow_stuff));
  NEW_SHAPEVEC(ellipses2, EllipseData, EllipseData::extractEllipses(orange_stuff));
}

The code above extracts ellipses from both the orange and yellow regions of the image. Note in the results below that the two large orange objects were rejected because their shapes were not elliptical enough. The small orange object in the upper right corner was accepted as a possible ellipse.

Copying and Assignment

Unlike sketches, copying and assignment of shapes are both shallow operations. Why is this different than for sketches? Sketches need deep assignment for constants, as in A=1. And sketches are frequently combined in arithmetic expressions; operators like A+=B only make sense if they're deep.

Shapes aren't subject to arithmetic, but we frequently manipulate them by selecting from among a set (actually a vector) of shape objects. Assignment is therefore most useful if it's shallow. So assignment for shapes is like the bind() function for sketches. If deep copying is needed, the expression A->copy()returns a new shape pointing to a deep copy of shape A, i.e., a new instance of LineData, EllipseData, etc.

 
 Exercises 


 Find all the orange ellipses in an image, then construct a set of
lines joining the centroids of those ellipses.  (Every shape provides
a getCentroid() function.)

 Find the longest line in the image.  Then find all ellipses
that touch that line.

 Show the robot two parallel lines, of different lengths.  Extract
those lines from the image.  Generate two more line shapes joining the
corresponding endpoints of the parallel lines; now you have four lines
forming a quadrilateral.  Generate a boundary sketch from the lines by
taking their renderings and or'ing them together.  Find the interior of
the quadrilateral using visops::fillInterior().





 The Shape Data Structures 










Prev: Sketch Primitives
Up: Visual Routines
Next: Shape Predicates


    

    Dave Touretzky


Last modified: Wed Jan 26 01:16:47 EST 2011

Basic shapes:	PointData, LineData, EllipseData
Complex shapes:	PolygonData, BlobData, MarkerData
3-D shapes:	SphereData, BrickData
Robot shape:	AgentData (robot position and orientation on the world map)

Length	Distance between endpoints; ignores valid/active flags.
Orientation	Since lines are symmetric, orientations range between 0 and pi. The slope is the tangent of the orientation.
Normal vector (rho,theta)	This is the endpoint of a vector from the origin that intersects the line at a right angle. It is expressed as a distance rho (always positive) and an angle theta (0 to 2 pi).

leftPt(), rightPt()	leftPt() returns the leftmost of the two endpoints based on their X coordinates; rightPt() returns the rightmost. If the line is vertical the choice is arbitrary, but the two functions will always return different endpoints.
topPt(), bottomPt()	topPt() returns the topmost of the two endpoints based on their Y coordinates (smaller values = topmost); bottomPt() returns the botommost. If the line is horizontal the choice is arbitrary, but the two functions will always return different endpoints.
leftPtShape(), rightPtShape(), topPtShape(), bottomPtShape()	These functions return a Shape<PointData> instead of a raw EndPoint. The parent is set to the line object.
isHorizontal(), isVertical()	A line is considered to be horizontal if its slope is no greater than 60 degrees; it is vertical if its slope is no less than 30 degrees. Diagonal lines (slopes between 30 and 60 degrees) satisfy both predicates.
firstPt(), secondPt()	If the line satisfies isHorizontal(), its first point is the leftmost endpoint. Otherwise its first point is the topmost endpoint. The second point is defined similarly.
firstPtShape(), secondPtShape()	Returns the first or second point as a Shape<PointData> rather than a raw EndPoint.
firstPt(otherline), secondPt(otherline)	These functions are useful when comparing two lines that might be just on the cusp of satisfying the horizontal test; hence one could pass the test while the other fails. To enforce agreement, we use one line to make the horizontal/vertical decision for both. If otherline satisfies isHorizontal(), this line's first point is the leftmost endpoint; otherwise this line's first point is the topmost endpoint. The second point is defined similarly.