For distributed robotic applications that require robots to share sensor information (e.g. mapping, surveillance, etc.) it is critical to know the position and orientation of the robots with respect to each other. Without knowing the position and orientation of the sensors, it becomes impossible to interpret the sensor data in a global frame of reference and integrate it with the data coming from other robots. Moreover, the Millibots require position knowledge to move to predetermined locations, avoid known obstacles, or reposition themselves for maximum sensor efficiency.

Conventional localization systems do not offer a viable solution for Millibots. Many robotic systems rely on Global Positioning Systems (GPS) and compass for determining their position and orientation in a global frame of reference. However, due to its size, limited accuracy, and satellite visibility requirements, GPS is not appropriate for the small Millibots that operate mostly indoors. Dead reckoning, another common localization method, generally suffers from accuracy problems due to integration errors and wheel slippage. This is even more pronounced for Millibots that rely on skid steering for which track slippage is inherent to the steering mechanism. Conversely, other localization systems that are based on landmark recognition or map-based positioning require too much computing power and sensing accuracy to be implemented on Millibots.

To overcome the problems encountered in the implementation of existing localization methods for a team of Millibots, we have developed a novel method that combines aspects of GPS, land-mark based localization, and dead reckoning. The method uses synchronized ultrasound pulses to measure the distances between all the robots on a team and then determines the relative positions of the robots through trilateration. Similar systems have been developed and are even commercially available (e.g. through IS Robotics). However, they are both too large and too expensive for operation on Millibots. Moreover, the system described in this article is more flexible because it does not require any fixed beacons with known positions, which is an important relaxation of the requirements when mapping and exploring unknown environments.

The Millibot localization system is based on the trilateration, i.e., determination of the position based on distance measurements to known landmarks or beacons. GPS is an example of a trilateration system; the position of a GPS unit on earth is calculated from distance measurements to satellites in space. Similarly the Millibot localization system determines the position of each robot based on distance measurements to stationary robots with known positions.

The Millibot localization system uses ultrasound pulses to measure the distances between robots. We designed a localization module that can serve either as a beacon or as a localization sensor. Initially, at least three Millibots serve as beacons, while the remaining robots are configured as receivers. Periodically, each beacon simultaneously emits a radio frequency (RF) pulse and an ultrasonic pulse. As is illustrated in Figure 3, The RF pulse, traveling at the speed of light (3´108 m/s), arrives at all receivers almost instantaneously. The ultrasonic pulse, on the other hand, traveling only at 343 m/s (assuming 20°C air temperature) arrives at the receiver delayed by a time proportional to its distance to the beacon. Each Millibot measures this delay, using the RF pulse for synchronization, and converts it to a distance measurement by multiplying with the speed of sound. A team leader coordinates the pining sequence to ensure that beacon signals from multiple robots do not interfere with one another.

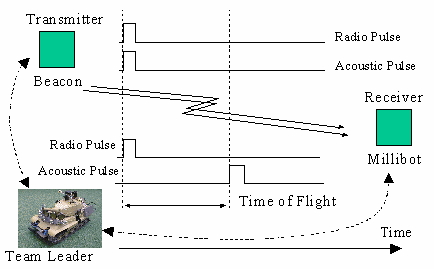
Figure 3: Ultrasonic distance measurement.

After all the beacons finish pinging, every Millibot has a set of distance measurements from its current position to each beacon position. This information is sequentially transmitted to the host computer, which determines the actual position of every Millibot using an Extended Kalman Filter (EKF). In the future, we plan to calculate the Millibot positions on the local processor of each Millibot. However, currently the processor does not have the necessary computation power to perform these floating-point computations.

To produce and detect beacon signals, each Millibot is equipped with a modified, low-cost ultrasonic transducer. This transducer can function either as a receiver or as an emitter. For localization to be effective, it is important that the sensor can detect signals coming from any direction around the Millibot. As is illustrated in Figure 4, an ultrasonic transducer is positioned to faces straight up and all incoming and outgoing sound waves are reflected by an aluminum cone. The result is a 360 degree coverage in the horizontal plane. The ultrasonic transducer with reflector is about 2.5cm tall. It can measure distances up to 3m with a resolution of 8mm while consuming only 25mW. The construction and design of this detector was paramount in achieving a beaconing system at this scale.

Figure 4: The acoustic reflector.

To provide noise rejection and develop a model dependant estimation of position and orientation, an Extended Kalman Filter (EKF) is applied to the distance data of each Millibot. The EKF is a modification of the Linear Kalman Filter and can handle nonlinear dynamics and nonlinear measurement equations. The EKF is an optimal estimator that recursively combines noisy sensor data with a model of the system dynamics. Inputs to the EKF include distance measurements between the robot and the beacons as well as the velocities of both tracks. The dynamics in this application are the kinematic relationships that express the change in position of the robot as a function of the track speeds. The EKF fuses this dead reckoning data with the beacon measurements. The two inputs complement each other to produce an optimal estimate of the robot's position and orientation.

As an intermediate result, the EKF computes the difference between the predicted and observed measurements, called the innovation. In our implementation, we use the innovation to reject inaccurate distance measurements. When there does not exist a direct line of sight between a beacon and a Millibot, the sound pulse may still reach the Millibot by reflecting off obstacles, walls, or other robots. This phenomenon is called multi-path. Multi-path measurements result in an abnormally large innovation and are rejected.

Consider the nonlinear system to be estimated:

where x(k) represents the state vector, u(k) represents external inputs to the system, and w(k) represents the state noise. This is a zero mean, white random sequence with covariance Q(k) .

The nonlinear measurement equation has the form

where z(k) represents the measurements vector and v(k) represents the measurement noise. This noise is also a zero mean, white random sequence with covariance R(k) .

The Kalman filtering process was designed to estimate the state vector in a linear model. For nonlinear models, a linear Taylor approximation of the system is computed at every time step. The measurement model h[k,x(k)] is linearized about the current predicted state vector . The plant model is linearized about the current estimated state vector .

The EKF consists of a prediction and an update step:

Prediction:

Where is the predicted state at the time of the next measurement, and P(k+1|k) is the state prediction covariance. fx(k) is the Jacobian of with respect to the state x.

Update:

Where S(k+1) is the innovation covariance, K(k+1) is the filter gain, is the updated state estimate and P(k+1|k+1) is the updated state covariance. hx(k) is the Jacobian of with respect to the state x.

Consider the robot representation shown in the following Figure 5. We denote the velocities of the left and right tracks by VL and VR respectively.

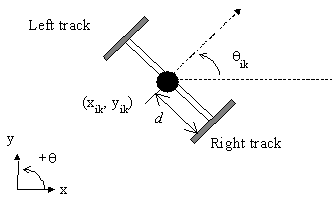
Figure 5: Representation for the robot kinematics.

The kinematic discrete time model is given by

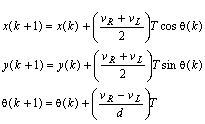
where T is the sample time interval. The state to be estimated for the ith robot is This model is a first order approximation that works well for small T and low track speeds.

The measurement model for the ith robot is given by

where is the distance measurement from the beacon source q to the ith robot, and vq represent zero-mean Gaussian measurement noise.

An initialization routine determines the positions of all the robots at start-up. The EKF requires at a minimum, that the position of the beacon robots are known with respect to one another. To determine initial positions, the team leader will collects distance measurements between any arbitrary pair of robots by pinging the beacon of each robot and collecting the measurements from all the other robots. The team leader then assigns the position (0,0) to an arbitrarily robot. A second robot is assigned a position on the X-axis. This defines a frame of reference in which the position of all other robots is determined through trilateration. However, based on distance measurements alone, there remains an ambiguity about the sign of the Y coordinates of each robot. To resolve this ambiguity, the team leader commands one robot to follow a short L-shaped trajectory and recomputes distance. If the robot turned to the left, but the assigned coordinate system indicates a right turn, the sign of the Y-coordinates of all robots are reversed.

An important advantage of the Millibot localization system is that it does not rely on fixed beacons. Instead, a minimum of three Millibots (but not necessarily always the same three) serve as beacons at any time. The Millibots that serve as beacons remain stationary. The other robots can move around in the area that is within reach of the beacons. While they sense the environment, they can determine their position with respect to the current beacons. When the team has explored the area covered by the current beacons, other robots will become stationary and start serving as beacons. In this fashion, the team can move over large areas while maintaining good position estimates.

The localization algorithm is most accurate when the beacons are at the vertices of an equilateral triangle. When a team moves over a large distance, the beacon that is farthest removed from the goal will be replaced by a Millibot in a position closer to the goal and equidistant to the other two beacons. This leap-frogging approach allows a team to move forward, while always maintaining three stationary beacons in known locations.

For example, in a team of four robots, three robots establish the initial geometric formation. The fourth robot drives to the center of the formation and determines the angle to the group goal. Based on that angle it selects a path between two of the three robots that takes it closest to the goal. The robot continues on this path until it forms a new triangle with those same two robots. If no other robots are available, the robot farthest away breaks ranks and performs the same actions. The group slowly moves towards the goal while maintaining localization. When limited to four robots, only one robot is moving at any one time and the others are fixed to maintain a relative marker. However, robots not participating in the beacon formations are free to wander in and out of the formation to perform their sensing tasks. If more than four robots are available for operating as beacon sources, the formation can grow beyond two triangles at any one time to produce a formation highway. The advantage to building a highway is that robots free of the formation can move quickly back and forth along the triangle highway without having to wait for the formation to move.