
im = empty_image(12) make_square!(im,10) make_square!(im,6)


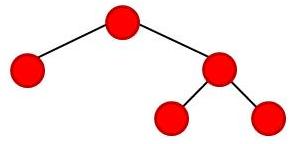
Suppose we want to write a function that takes a binary tree like this as input and plots it using the image data structure we've been experimenting with in this assignment. We can use a simple mathematical relationship to lay out the tree, as shown below:

Each node of the tree will be drawn in a box defined by start and finish values. Since our image is 7 pixels wide, initially start=0 and finish=6. When we draw a node in a box, we always draw it at the midpoint, mid = (start+finish)/2.
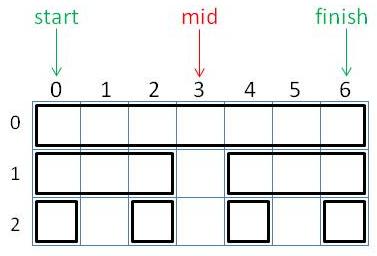
The root of the tree is at depth 0, and it is drawn at position mid = (0+6)/2 = 3. Tbis root is a nonterminal node, so it has two children, and each gets its own box on the level below. The left child's box runs from start to mid-1, and the right child's box runs from mid+1 to finish. So we see that at depth 1 we have a box occupying spaces 0-2 and a second box occupying spaces 4-6. We can recursively decompose these boxes too. For the left box at depth 1, mid=1 and the two boxes at depth 2 are at positions 0 and 2. For the right box at depth 1, mid=5 and the child boxes at depth 2 are at 4 and 6.
 Now that we know how our tree should be layed out, we can write a
recursive function to draw the tree. The tree [412, [268,
2000]] should appear as the image at right. The code below will
do the drawing, once you've completed the missing pieces marked by
"...". Rather than typing it in by hand, you can copy it from the
file draw_tree.rb. Notice that
draw_tree_helper contains a puts statement to help you debug
your recursive calls.
Now that we know how our tree should be layed out, we can write a
recursive function to draw the tree. The tree [412, [268,
2000]] should appear as the image at right. The code below will
do the drawing, once you've completed the missing pieces marked by
"...". Rather than typing it in by hand, you can copy it from the
file draw_tree.rb. Notice that
draw_tree_helper contains a puts statement to help you debug
your recursive calls.
Test your draw_tree function on the following examples:def draw_tree(tree) width = 7 # works for trees up to depth 2 image = empty_image(width) depth = 0 start = 0 finish = width-1 draw_tree_helper(tree,image,depth,start,finish) plot(image,20) end def draw_tree_helper(tree,image,depth,start,finish) puts "tree=#{tree.inspect} depth=#{depth} start=#{start} finish=#{finish}" mid = (start + finish) / 2 # draw the current node image[depth][mid] = [255,0,0] if tree.kind_of?(Array) then # recursively draw the children: FILL IN THE "..." PART draw_tree_helper(tree[0], ...) draw_tree_helper(tree[1], ...) end end
draw_tree("eureka")
draw_tree(["do", ["re","mi"]])
draw_tree([["do","re"], "mi"])
draw_tree([["fee","fie"], ["foe","fum"]])