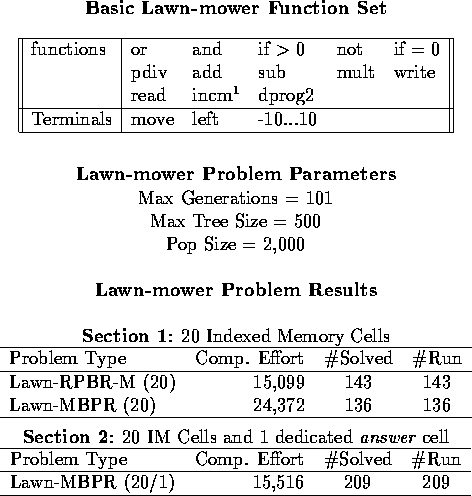
Table 2: The Lawn-mower Problem
The next benchmark problem we chose for further validation of the MBPR results shown in the previous section was the lawn-mower problem. The lawn-mower problem was chosen for two important reasons. The first is that, as will be described, this version of the lawn-mower problem requires the use of memory. This required use of memory makes it possible to at least partly separate the MBPR paradigm from the general helpfulness of memory (table 1). The second reason was to pick a problem with more complexity than the 5-Parity problem and with a much richer function set.

Table 2: The Lawn-mower Problem
A version of the lawn-mower problem is described in [Koza1992]. The basic concept is that there is a lawn-mower in an 8x8 toroidal grid world. In our version of the problem, the mower only moves once per execution of the tree, and is allowed 200 time steps. If the value returned is less than zero, then the mower turns left. If the value is greater than zero, then it moves forward and mows. If the return value is zero, it does nothing. The lawn-mower's goal is to mow as much of the world as possible during those 200 time steps. Since it receives no sensory input, it must rely on its memory to help it create a path that hits most or all of the grid positions. This description (and the function set shown in table 2) should make it clear that this problem only shares surface level details with the lawn-mower problem in [Koza1992]. The main differences are: no state except indexed memory (i.e., no progn), one move at a time (i.e. one move per tree evaluation), and no jumping allowed.
The lawn-mower problem (results for which are shown in
table 2:1) was set up so that memory was
required![]() . We see that the MBPR takes 1.62 times as much computational
effort as RPBR. This is surprising given that the programs are using
their memory anyway. One potential explanation for this is that
because this is actually a memory critical problem, and zero is a very
likely value to occur
. We see that the MBPR takes 1.62 times as much computational
effort as RPBR. This is surprising given that the programs are using
their memory anyway. One potential explanation for this is that
because this is actually a memory critical problem, and zero is a very
likely value to occur![]() , different program pieces may
initially ``fight'' for control of memory cell 0: some to store the
answer, and others to keep track of the mowing movements.
, different program pieces may
initially ``fight'' for control of memory cell 0: some to store the
answer, and others to keep track of the mowing movements.
The above hypothesis suggests the following experiment: continue to use 20 indexed memory cells, but introduce one new dedicated memory cell for the MBPR ``answer.'' To dedicate this memory cell, a new function was introduced into the function set: WRITE-ANSWER. WRITE-ANSWER takes one parameter, the value, and stores that value in the dedicated memory cell. The results of this experiment are shown in table 2:2. The addition of this dedicated memory cell has successfully reduced the computational cost of the MBPR runs to almost exactly that of the RPBR runs. This change in computational cost demonstrates that contention over the ``answer'' position in indexed memory (memory cell 0) was indeed the expensive aspect of the MBPR runs shown in table 2:1. In short, MBPR does not reduce computational effort in this domain, but does not increase it either.