Fast T3D Array Transposes based on the CMU direct deposit model

Memory access pattern in transposes

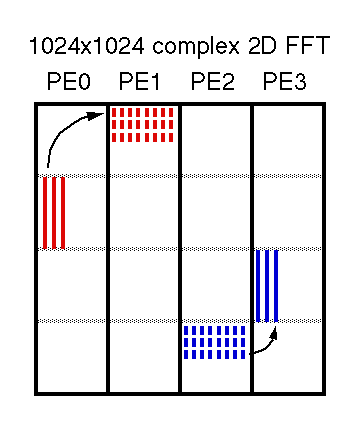
The transpose routines can choose between more contiguous loads with strided stores (depicted in red), or strided loads with more contiguous stores (depicted in blue). The alpha processor used in the Cray T3D has good support for strided stores (efficient write-back queue) and relatively poor support for strided loads (cache, and read-ahead logic don't help much). Therefore our routines prefer contiguous loads.

Performance characterization

Summary:

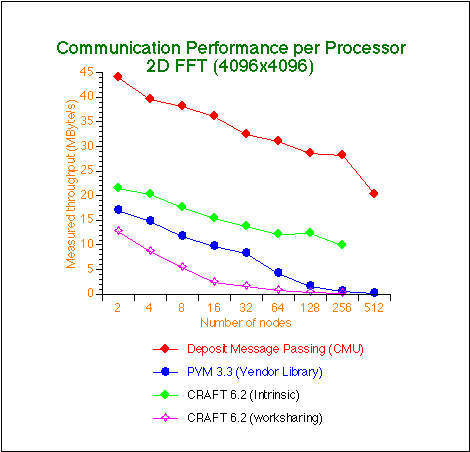
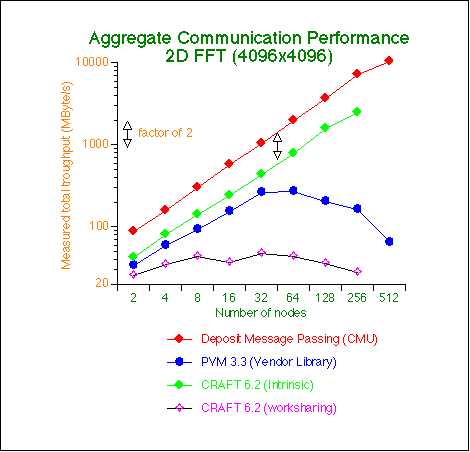
Note: The break down to 22 MByte per processor in the direct deposit for 512 element is attributed to irregularities in the T3Ds current routing table. These routes render our congestion control scheme useless. So far Cray Research seemed very reluctant to give us details why routes are not following a proper e-cube scheme.

The second graph shows how communication performance affects scalability of the transpose operations. The direct deposit and the CRAFT intrinsic transpose scale fine up to 256 or even 512 nodes. The PVM performance falls apart above 32 or 64 processors, while worksharing does not scale far beyond 8 processor.

Note that on the log-log scale the quarter inch between the two curves means a factor of two performance difference.

Code examples of Direct Deposit, PVM and CRAFT versions

Deposit and PVM, common declarations:

#define P  256
#define NM 4096+4
#define N 4096
#define RM (NM/P)
#define R (N/P)

#pragma _CRI cache_align a,b

static doublecomplex a[RM][NM];     /* input matrix */
static double fill[4];
static doublecomplex b[RM][NM];     /* input matrix */

Direct deposit implementation:

/* Pseudocode, real routines contain a number of memory system 
 * optimization such as unrolled loops, folded constants etc... 
 */
barrier();
for (j=0; j<P; j++) {
  barrier();                        /* congestion control */
  j0=comm_schedule[j];
  i0=my_cell_id;
  b0=shmem_init(b,a,1,j0);
  for (l=0; l<R; l++) {
    for (m=0; m<R; m++) {           /* copy loop w. remote stores */
      b0[m][i0*R+l].r=a[l][j0*R+m].r;
      b0[m][i0*R+l].i=a[l][j0*R+m].i;
    }
  }
}
barrier();
shmem_udcflush();                   /* restore cache consistency */

PVM 3.3 implementation

/* Pseudocode, real routines contain a number of memory system 
 * optimization such as unrolled loops, folded constants etc... 
 */
for (j=0; j<P; j++) {                /* pack buffers */
  for (l=0; l<R; l++) {
    for (m=0; m<R; m++) {
      af[j][m*R+l].r=a[l][j*R+m].r;
      af[j][m*R+l].i=a[l][j*R+m].i;
    }
  }
}
for (j=0; j<P; j++) {                /* do sends */
  pvm_initsend(0);
  pvm_pkdouble(af[j],R*R*2,1);
  pvm_send(j,0);
}
for (j=0; j<P; j++) {                /* do receives */
  pvm_recv(j,0);
  pvm_upkdouble(bf[j],R*R*2,1);
}
for (j=0; j<P; j++) {                /* unpack buffers */
  for (m=0; m<R; m++)
    for (l=0; l<R; l++) {
      a[m][j*R+l].r=bf[j][m*R+l].r;
      a[m][j*R+l].i=bf[j][m*R+l].i;
    }
  }
}

CRAFT, common declarations:

      real a(N,N)
      real b(N,N)

      intrinsic transpose

cdir$ cache_align a,b
cdir$ shared a(:,:block)       
cdir$ shared b(:,:block)       

CRAFT worksharing transpose code:

      do i = 1,N 
cdir$ doshared (j) on b(i,j)       
         do j = 1,N 
            b(i,j)=a(j,i)
         enddo
      enddo

CRAFT worksharing transpose code:

      b= TRANSPOSE(a)

Reference to further literature on the topic

See also manual page entry .

See also Fx compiler related papers, see fx-papers .