We implemented the Suffix Array(SA) Construction Skew algorithm in CUDA on GPU platform to achieve good speedup and compared performance with PBBS Suffix Array benchmark serial and parallel SA implementation. Our GPU version provides as a part of PBBS Suffix Array benchmark. Our SA implementation in CUDA achieves 10-20x speedup on standard large datasets, which contain more than 100 Million characters. Suffix array is a sorted array of all suffixes of a string. This indexing data structure is widely used in data compression algorithms and Biological DNA sequences. Based on Mrinal13's analysis, DC3/skew algorithm proposed by Karkkainen and Sanders (2003) is most suitable to be implemented in GPU, because all its phases can be efficiently mapped to a data parallel hardware. It runs in linear time and has successfully been used as the basis for parallel and external memory suffix array construction algorithms. The key idea of DC3/skew algorithm is shown in the following graph. In Guy Blelloch's Problem Based Benchmark Suite, Suffix Arrays based on DC3/skew algorithm have the benchmark in both serial and parallel mode.

The input is an ascii string and the output is the Suffix Array in an integer sequence. The basic idea is:

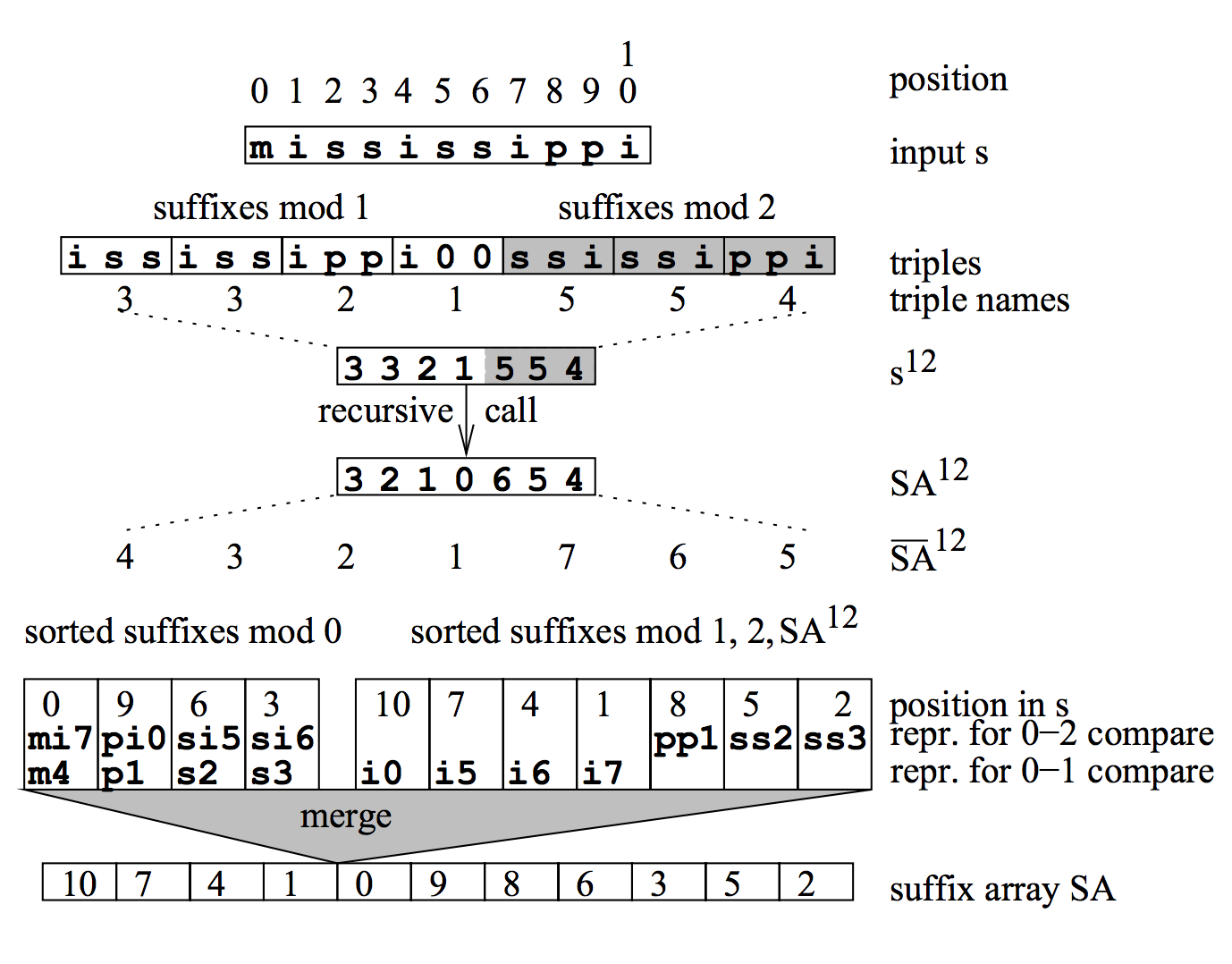
1. split the original string into 2 sets, positions i mod 3 is zero and positions i mod 3 is non-zero.
2. recursively sort suffixes beginning at positions i mod 3 is not 0.
3. sort the remaining suffixes using the information obtained in step one.
4. merge the two sorted sequences obtained in steps one and two.

As shown in figure, Skew Algorithm is broken up into several steps and every step could be parallelized more or less. Among those, radixSort and MergeSort steps is the most time-consuming part and we should pay additional attention to the optimization of these two parts. For the other parts, the work would be data transformation on a large array, which could be parallized using several kernels. However it is hard to break the ordering and recursion logic because the following steps of the algorithm depends on the previous results. The most challenging part here is how to parallelize radixSort(s0) which is to sort s0 based on previous sorted s12 results.

• Technologies: CUDA on GHC 3K Nvidia 480X GPU platform
• Skew Algorithm pseudocode and how to make it parallelize it in CUDA:
  (Based on the paper "Parallel suffix array and least common prefix for the GPU" by Mrinal Deo and Sean Keely.)

          	
          		computeSA(int *T, int *SA, int length)
          		{
          		    initMod12();  
          		    radixSort(s12);  // lsb radix 1st Character                     kernel1
          		    radixSort(s12);  // lsb radix 2nd Character
          		    radixSort(s12);  // lsb radix 3rd Character
          		    lexicRankOfTriplets();                                          kernel2
          		    if (!allUniqueRanks)
      			        computeSA();                                                recursion
      			        storeUniqueRanks();                                         kernel3
      			    else
      			        computeSAFromUniqueRank();                                  kernel4
      			    radixSort(s0)                                                   kernel1
      			    mergeSort(s0, s12)                                              kernel5
          		}
          	
          

• Basically we use the CUDA Thrust Library which provide powerful APIs such as thrust::transform, thrust::sort, thrust::merge and etc. For those kernels which is not applicable to be written efficiently in thrust methods, we write our own kernel to make it best efficient.
• We do not change the original serial algorithm skeleton to enable better mapping because each step requires strict ordering.
• Start code: our implementation in CUDA is based on the PBBS SA parallelKS code on multi-core platform.

• Complex Algorithm. Because Skew algorithm itself is very tricky and highly optimized so it is hard for CUDA version implementation. We choose to use Thrust Library to help us implement the algorithm. The implementation challenge here is to carefully design the host and memory allocation and use optimized thrust methods such as fusion and self-written kernel to parallelize each single step. Also we tried hard to reduce the number of kernels and combine multiple steps into one kernel to accelerate the process and reduce overhead.
• Merge Function. At first, we use the thrust::merge to do the final step. However, we found a problem using thrust::merge directly, so we write our own version of merge in CUDA. It works very well. The algorithm we choose for the merge is very simple: we separate the input string A and B into multiple segments using binary search; and then each block merge two of the segments and put the result into the result array; in each block, the segment is also splitted into much smaller ones for each thread to work on.
• Memory. If the input sequence is very large in million size, we may run into a "out of memory" problem. Because the algorithm here is a recursive one and in each step we have to store some additional information that is used in the GPU kernels and thrust functions. We have to carefully allocate memory in the program and free them frequently. A good way is to use the host memory as a temp store, even though it may slow down the program. It is a tradeoff between performance and supported data set size.

First we came up with wrong answer using thrust:merge method and we replace that with sequencial code and it works! But it brings the bottleneck -- merge part. Then we address this serial part and implemented our version of merge in CUDA which significantly improve the performance of merge. We also made some optimization on kernel3 and kernel4 to reduce the number of kernels. During implementation, we also came up with some out of memory problem. We found that for small datasets our program works well but it will abort for large datasets over 1 million characters. To address the memory issue, we tried hard to manually save the device memory space by cudaFree() frequently and in advance. Finally we came to the current version. We use the standard datasets in PBBS benchmark.

• trigramString: A trigram string of length n=10,000,000.
• chr22.dna: A DNA sequence, about 34 million characters.
• etext99: 105 Million characters, text from Guttenberg.
• wikisamp: 100 million characters, a sample from wikipedia's xml source files.

Here are results of our CUDA SA performance compared with the PBBS serial and parallel on GHC 3K machine. We have optimizied the merge part which is hard to parallelize well in CUDA. We change the trust::merge to local version and overcome the merge bottleneck by reducing the merge part time to a speedup of 7x than serial version merge. Our final version has the 18x speedup on etext99 and 13x speedup on wikisample dataset. As we expect, the larger dataset is, the more speedup our GPU SA algorithm can achieve.

Now radixSort and mergeSort consume about half of the overall time. Overall, we think now our speedup on GPU is very cool. For future work, we can optimize the thrust::sort, which is the radix sort part, to achieve some more improvement.

• Our current implementation is not linear scalable on GPU because the serial order to kernels and the recursive algorithm. The algorithm structure limits the speedup upper bound. The skew algorithm does not allow us to break up the serial order to parallelize multiple steps.
• Secondly, to address the out of memory problem, we need to transfer data between host and device for multiple times. This is also a large portion of overall time, which we need to do so to make correct result. As shown in the time distribution graph, those memory transfer time is included in the "other" part.
• Finally, the thrust::sort library to do radixSort is not efficient enough. Our sorting is a more specific progress and the max key value is not that big. The current thrust::sort doesn't take the max key into consideration. We would expect some performance improvement if we implemented our own version of radixSort which considers the max key value.

• Ge Gao: Implement skeleton code, the kernels and parallelized merge part in CUDA.
• Chaomin Yu: Implement serial merge part, run experiments and report writeup.

Karp, Richard M.; Miller, Raymond E.; Rosenberg, Arnold L. (1972). "Rapid identification of repeated patterns in strings, trees and arrays". Proceedings of the fourth annual ACM symposium on Theory of computing - STOC '72. p. 125.

Farach, M. (1997). "Optimal suffix tree construction with large alphabets". Proceedings 38th Annual Symposium on Foundations of Computer Science. p. 137.

Karkkainen, Juha, and Peter Sanders. "Simple linear work suffix array construction." Automata, Languages and Programming. Springer Berlin Heidelberg, 2003. 943-955.

Mrinal Deo and Sean Keely. 2013. Parallel suffix array and least common prefix for the GPU. In Proceedings of the 18th ACM SIGPLAN symposium on Principles and practice of parallel programming (PPoPP '13). ACM, New York, NY, USA, 197-206.

Problem Based Benchmark Suite, Suffix Arrays (SA)