We introduce the concept of maximum entropy through a simple example. Suppose
we wish to model an expert translator's decisions concerning the proper French
rendering of the English word in. Our model 
of the expert's
decisions assigns to each French word or phrase f an estimate, 
, of
the probability that the expert would choose f as a translation of in.
To guide us in developing 
, we collect a large sample of instances of the
expert's decisions. Our goal is to extract a set of facts about the
decision-making process from the sample (the first task of modeling) that will
aid us in constructing a model of this process (the second task).
One obvious clue we might glean from the sample is the list of allowed translations. For example, we might discover that the expert translator always chooses among the following five French phrases: {dans, en, à, au cours de, pendant}. With this information in hand, we can impose our first constraint on our model p:
This equation represents our first statistic of the process; we can now proceed
to search for a suitable model which obeys this equation. Of course, there are
an infinite number of models 
for which this identity holds. One model
which satisfies the above equation is 
; in other words, the model
always predicts dans. Another model which obeys this constraint predicts
pendant with a probability of 
, and à with a probability
of 
. But both of these models offend our sensibilities: knowing only that
the expert always chose from among these five French phrases, how can we
justify either of these probability distributions? Each seems to be making
rather bold assumptions, with no empirical justification. Knowing only that the
expert chose exclusively from among these five French phrases, the
most intuitively appealing model is
This model, which allocates the total probability evenly among the five possible phrases, is the most uniform model subject to our knowledge. (It is not, however, the most uniform overall; that model would grant an equal probability to every possible French phrase.)
We might hope to glean more clues about the expert's decisions from our
sample. Suppose we notice that the expert chose either dans or en
30% of the time. We could apply this knowledge to update our model of the
translation process by requiring that 
satisfy two constraints:
Once again there are many probability distributions consistent with these two
constraints. In the absence of any other knowledge, a reasonable choice for
is again the most uniform--that is, the distribution which allocates
its probability as evenly as possible, subject to the constraints:
Say we inspect the data once more, and this time notice another interesting fact: in half the cases, the expert chose either dans or à. We can incorporate this information into our model as a third constraint:
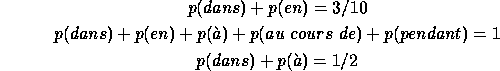
We can once again look for the most uniform 
satisfying these constraints,
but now the choice is not as obvious. As we have added complexity, we have
encountered two problems. First, what exactly is meant by ``uniform,'' and how
can one measure the uniformity of a model? Second, having determined a
suitable answer to these questions, how does one find the most uniform model
subject to a set of constraints like those we have described?
The maximum entropy method answers both these questions. Intuitively, the
principle is simple: model all that is known and assume nothing about that
which is unknown. In other words, given a collection of facts, choose a model
which is consistent with all the facts, but otherwise as uniform as
possible. This is precisely the approach we took in selecting our model 
at
each step in the above example.