Experimenting with MICRO-HILLARY

To test the effectiveness of the MICRO-HILLARY algorithm, we experimented with it in various domains. Most of the experiments were done in the 15-puzzle domain. The basic operators in this domain are Up, Down, Left and Right, indicating the direction in which the empty tile ``moves''. The heuristic function, which we denote by RR, is similar to the one used by Iba [10] and by Korf [16]. The function contains three factors that are ordered lexicographically: the total number of tiles minus the count of tiles consecutively placed in a left-to-right, top-to-bottom, row-by-row order, the Manhattan distance of the first tile that is not in place to its destination, and the Manhattan distance of that tile from the empty square. 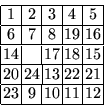Consider, for example, the following puzzle:

$$\renewcommand{\arraystretch}{1.0}\setlength{\arraycolsep}{0.... ...22 & 21 \\ \hline 23 & 9 & 10 & 11 & 12 \\ \hline \end{array}$$

. There are 8 tiles placed in the specified order; therefore, the first component is 24-8=16. The first tile not in its goal location is 9, so the second component (the Manhattan distance between 9 and its destination) is 5. The third component (the Manhattan distance between 9 and the empty square) is 2. This function essentially tells the problem solver to try ordering the tiles row by row.⁶ This heuristic encodes subgoaling of puzzle problems which is quite natural, and is immediately inferred by most people trying to solve the sliding-tile puzzle. However, many people have difficulties solving the puzzle even after inferring this heuristic. We will also report results for other heuristic functions such as the sum of Manhattan distances.

We begin by describing the experimental methodology used, and continue with a description of the experiments performed.