The Trains domain present a somewhat different variation on our original conclusions. The Trains domain involves a set of locations and objects, and the goal is to transport various objects from specific starting locations to specified destinations. Gerevini and Schubert studied three Trains problems. All of our strategies failed to successfully complete the hardest of these (Trains3) within either the 100,000 node or the 1000 second limit. Moreover, many of them also failed on the second hardest (Trains2). Caution must therefore be taken in interpreting the results, as there are a limited number of data points.

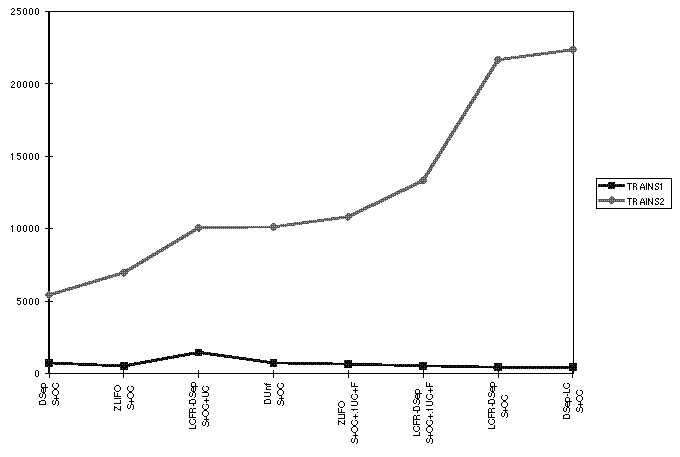
Figure  gives the node counts for the Trains domain, with
preconditions inserted in the default order. We
only show the strategies that were able to solve both Trains1 and Trains2.
These results are
closer to what we would have predicted from the basic problem set than
were the results with the Tileworld. In particular, LCFR-DSep does
very well, generating much smaller search spaces than LCFR.
However, it does slightly worse than ZLIFO. Recall that we saw the
same pattern of performance on a subset of the basic problems,
specifically on the Get-Paid/Uget-Paid problems. There, LCFR-DSep
again improved on LCFR, but did not generate as small search spaces as
ZLIFO. It turns out that there are similar factors influencing both
sets of problems, and it is instructive to consider in some detail the
planning done by ZLIFO and LCFR-DSep for the Get-Paid/Uget-Paid
problems to understand what is occurring.
gives the node counts for the Trains domain, with
preconditions inserted in the default order. We
only show the strategies that were able to solve both Trains1 and Trains2.
These results are
closer to what we would have predicted from the basic problem set than
were the results with the Tileworld. In particular, LCFR-DSep does
very well, generating much smaller search spaces than LCFR.
However, it does slightly worse than ZLIFO. Recall that we saw the
same pattern of performance on a subset of the basic problems,
specifically on the Get-Paid/Uget-Paid problems. There, LCFR-DSep
again improved on LCFR, but did not generate as small search spaces as
ZLIFO. It turns out that there are similar factors influencing both
sets of problems, and it is instructive to consider in some detail the
planning done by ZLIFO and LCFR-DSep for the Get-Paid/Uget-Paid
problems to understand what is occurring.
Like the Trains domain problems, the Get-Paid/Uget-Paid problems involve moving particular objects to specified locations. In the Get-Paid/Uget-Paid domain there are three objects: a paycheck, a dictionary, and a briefcase. As generally formulated, in the initial state all three are at home, and the paycheck is in the briefcase. The goal is to deposit the paycheck at the bank, bring the dictionary to work, and have the briefcase at home. Both the dictionary and the paycheck can be moved only in the briefcase. For a human, the solution to this problem is obvious. The dictionary must be put into the briefcase, and it must then be carried to work, where the dictionary is taken out. The briefcase must then be carried home. In addition, a stop must be made at the bank, either on the way to work or on the way home, at which point the paycheck must be taken out of the briefcase and deposited.
ZLIFO and LCFR-DSep take different paths in solving this problem. ZLIFO begins by forming plans to get the paycheck to the bank and the dictionary to work. These goals are selected first because they are forced: there is only one way to get the paycheck to the bank (carry it there), and similarly only one way to get the dictionary to the office (carry it there). In contrast, there are two possible ways to get the briefcase home: either by leaving it there (i.e., reusing the initial state) or by carrying it there from somewhere else (i.e., adding a new step). The LIFO mechanism then proceeds to complete the plans for achieving the goals of getting the paycheck to the bank and the dictionary to work, before beginning to work on the remaining goal, of getting the briefcase home. At this point, that goal is easy to solve. All that is needed is to plan a route home from wherever the briefcase is at the end of these two errands.
LCFR-DSep, like ZLIFO, begins by selecting the forced goals of getting
the dictionary to the office and getting the paycheck to the bank.
However, instead of next completing the plans for these goals,
LCFR-DSep continues to greedily select least-cost flaws, and thus
begins to work on achieving the goal of getting the briefcase home.
Unfortunately, at this point it is not clear where the briefcase needs
to be moved home from, and hence LCFR-DSep begins to engage in a
lengthy process of ``guessing'' where the briefcase will be at the end
of the other tasks, before it has planned for those
tasks.
The key decision for the Get-Paid/Uget-Paid domain--and, as it turns out, for the Trains domain--is related to, but subtly different from the key decision in the Tileworld domain. For Get-Paid/Uget-Paid and Trains, the key insight for the planner is again that there is an important temporal ordering between goals. The goal of getting the briefcase home is going to have to be achieved after the goal of taking the dictionary to work. However, recognition of this constraint is not affected by separable-threat delay, as it was for the Tileworld. Instead, what happens in these domains is that a higher-cost flaw interacts with a lower-cost one, causing the latter to become fully constrained.
It is tempting to think that here finally is a case in which a LIFO-based strategy is advantageous. After all, for this example, by completely determining what you will do to achieve one goal, you make it much easier to know how to solve the another goal. But the use of ZLIFO (or an alternative LIFO-based strategy) does not guarantee that the interactions between high- and lower-cost flaws will be exploited. In particular if the interactions are among two or more unforced flaws, then the order of the goals in the agenda can lead ZLIFO to make an inefficient choice. Thus, when we modified the problem so that the briefcase was at work in the initial state, ZLIFO and LCFR-DSep both solved the problem very quickly (178 nodes for ZLIFO and 157 for LCFR-DSep). Note that this modification removes the problematic interaction between a low-cost and a high-cost flaw.
Finally, note that the effectiveness of the LIFO strategies is again
heavily dependent on the the order in which preconditions are entered
onto the open list. Figure  gives the node counts for
the Trains domain with reverse precondition insertion. We once again
plot only the strategies that can solve both Trains 1 and
Trains2. In this case, there
are only two such strategies:
LCFR-DSep and DSep-LC.
The strategies that rely on
LIFO for open-condition selection, ZLIFO, DSep, DUnf-Gen, and UCPOP,
all do significantly worse than they did when the preconditions were
in the correct order. To the extent that LIFO helps in such domains,
it appears to be because of its ability to exploit the
decisions made by the system designers in writing the domain
operators, as suggested by Williamson and Hanks (1996).
gives the node counts for
the Trains domain with reverse precondition insertion. We once again
plot only the strategies that can solve both Trains 1 and
Trains2. In this case, there
are only two such strategies:
LCFR-DSep and DSep-LC.
The strategies that rely on
LIFO for open-condition selection, ZLIFO, DSep, DUnf-Gen, and UCPOP,
all do significantly worse than they did when the preconditions were
in the correct order. To the extent that LIFO helps in such domains,
it appears to be because of its ability to exploit the
decisions made by the system designers in writing the domain
operators, as suggested by Williamson and Hanks (1996).
