The Value of Separable-Threat


Next: The Need for Domain
Up: Experimental Comparison of Flaw
Previous: Comparing LCFR and ZLIFO
The Value of Separable-Threat Delay
Our first two analyses were essentially aimed at replicating earlier
results from the literature, namely the LCFR results and the ZLIFO
results. We next address the question of how to square these results
with one another.
Recall that LCFR and ZLIFO differ in two key respects. First, LCFR
treats all flaws uniformly, while ZLIFO distinguishes among flaw
types, giving highest preference to nonseparable threats, medium
preference to open conditions, and lowest preference to separable
threats. Second, while LCFR uniformly makes least-cost selections,
ZLIFO uses a LIFO strategy secondary to its flaw-type preferences
(but after giving preference to forced open conditions). The
comparisons made in Section  suggest that the use of a
LIFO strategy for unforced flaws should at best make little difference
in search-space size, and may possibly lead to to the generation of
larger search spaces. On the other hand, the first difference
presents an obvious place to look for a relative advantage for ZLIFO.
After all, what ZLIFO is doing is delaying separable threats, and Peot
and Smith demonstrated the effectiveness of that approach in their
DSep strategy.
suggest that the use of a
LIFO strategy for unforced flaws should at best make little difference
in search-space size, and may possibly lead to to the generation of
larger search spaces. On the other hand, the first difference
presents an obvious place to look for a relative advantage for ZLIFO.
After all, what ZLIFO is doing is delaying separable threats, and Peot
and Smith demonstrated the effectiveness of that approach in their
DSep strategy.
Peot and Smith's proof that DSep will never generate a larger search
space than UCPOP does not transfer to LCFR. There are planning
problems for which LCFR will generate a smaller search space than
DSep. Their proof relies on the fact that, in DSep, open conditions
will be selected in the same order, regardless of when threats are
selected. But the selection of a threat in LCFR can influence the
repair cost of an open condition (e.g., by promoting an action so that
it is no longer available as a potential establisher for some
condition), and this in turn can affect the order in which the
remaining open conditions are selected.
Nonetheless, despite the fact that one can't guarantee that
delaying separable threats will lead to a reduction in search-space
size, the motivation behind DSep is still appealing: separable threats
may often simply disappear during subsequent planning, which will
naturally lead to a reduction in search-space size. For this reason,
we implemented a slightly modified version of LCFR, which we called
LCFR-DSep, in which separable threats are delayed. Note that it is
relatively easy to do this in the UCPOP system, which provides a
switch, the dsep switch, which when turned on will automatically
delay the repair of all separable threats. As defined earlier in Table
 , the definition of LCFR-DSep is:
, the definition of LCFR-DSep is:
Our hypothesis was that if ZLIFO's reduction in search-space size were
largely due to its incorporating a DSep approach, then LCFR-DSep ought
to be ``the best of both worlds'', combining the advantages of LCFR's
least-cost approach with the advantages of a DSep approach.
On the basic problems, LCFR-DSep proved to have the smallest average node-count
%-overrun of on the basic problems of all of the strategies
tested. Moreover, this was true even when we reversed the order in
which the preconditions of an operator were added to the open list.
Figure  gives the average node-count %-overruns for both the
unmodified UCPOP v.4 (labeled ``default'') and the modified version in
which we reversed the precondition ordering (labeled ``reverse'').
Reversing the ordering does not effect the conclusion that LCFR-DSep
generates the smallest search spaces for these problems; in fact, in
general it had very little affect on the relative performance of the
strategies at all. The only notable exception, which we mentioned
earlier, is that the relative performance of LCFR and DUnf-Gen flips.
gives the average node-count %-overruns for both the
unmodified UCPOP v.4 (labeled ``default'') and the modified version in
which we reversed the precondition ordering (labeled ``reverse'').
Reversing the ordering does not effect the conclusion that LCFR-DSep
generates the smallest search spaces for these problems; in fact, in
general it had very little affect on the relative performance of the
strategies at all. The only notable exception, which we mentioned
earlier, is that the relative performance of LCFR and DUnf-Gen flips.
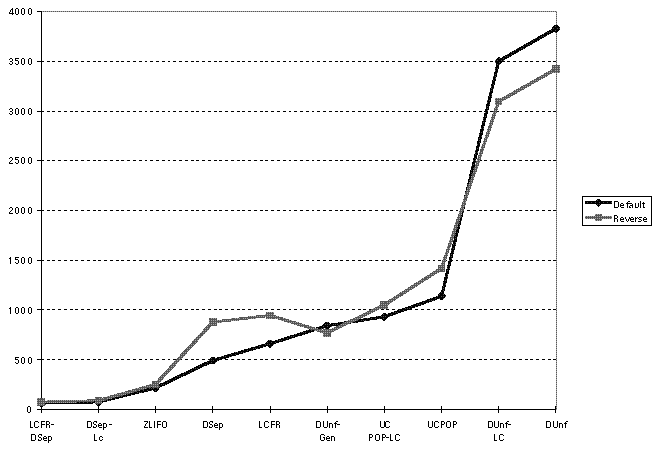 Figure: Basic Problems: Aggregate Performance for all Strategies
Figure: Basic Problems: Aggregate Performance for all Strategies
 Figure: Basic Problems: Node Counts for LCFR, ZLIFO, and DSep Strategies
Figure: Basic Problems: Node Counts for LCFR, ZLIFO, and DSep Strategies
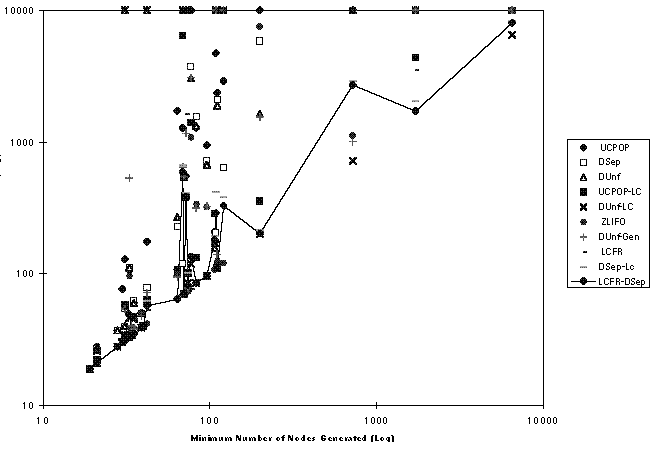 Figure: Basic Problems: Node Counts for all Strategies
Figure: Basic Problems: Node Counts for all Strategies
For more detailed comparison, we plot node counts on the basic
problems for LCFR, ZLIFO, and the Separable-Threat Delay strategies in
Figure
 . For ease of comparison, we again show the data
sorted by the difference between LCFR and ZLIFO's node counts. The
problems near the left-hand side of the graph are, again, those for
which LCFR generated a smaller search space than ZLIFO; the problems
near the right are those for which it generated a larger search space.
As can be seen, LCFR-DSep nearly always does as well as, or better
than LCFR. It does much better than ZLIFO on the problems that LCFR
is good at. And it also does much better than LCFR on the
problems that ZLIFO is good at. However, ZLIFO still outperforms
LCFR-DSep on this latter class of problems.
. For ease of comparison, we again show the data
sorted by the difference between LCFR and ZLIFO's node counts. The
problems near the left-hand side of the graph are, again, those for
which LCFR generated a smaller search space than ZLIFO; the problems
near the right are those for which it generated a larger search space.
As can be seen, LCFR-DSep nearly always does as well as, or better
than LCFR. It does much better than ZLIFO on the problems that LCFR
is good at. And it also does much better than LCFR on the
problems that ZLIFO is good at. However, ZLIFO still outperforms
LCFR-DSep on this latter class of problems.
Another view of the data is given in Figure  , the log-log
scatter plot for the basic problems, for all the strategies we studied.
This time we have highlighted LCFR-DSep's performance. Although there
are some problems for which it does not produce a minimal search
space, its performance on the individual problems is actually quite
good, consistent with its good aggregate performance.
, the log-log
scatter plot for the basic problems, for all the strategies we studied.
This time we have highlighted LCFR-DSep's performance. Although there
are some problems for which it does not produce a minimal search
space, its performance on the individual problems is actually quite
good, consistent with its good aggregate performance.
At least for the basic problems, augmenting the simple LCFR
strategy with a delay of separable threats reduces the search space as
expected. This in turn suggests that when LCFR generates a larger
search space than ZLIFO, that is due in large part to the fact that it
does not delay separable threats. ZLIFO's primary advantage relative
to LCFR seems not to be its use of a LIFO strategy for unforced threats,
but rather its separable-threat delay component. Combining
separable-threat delay with a least-cost approach yields a strategy
that tends to generate smaller search spaces than either strategy by
itself for the basic problem set. However, analysis of the Trains and
Tileworld problem sets reveals the situation to be a little more
complicated than the comparison of the basic problems would suggest,
as we discuss in the next section.


Next: The Need for Domain
Up: Experimental Comparison of Flaw
Previous: Comparing LCFR and ZLIFO
TOM Conversion
Wed Jun 25 17:40:58 EDT 1997
 suggest that the use of a
LIFO strategy for unforced flaws should at best make little difference
in search-space size, and may possibly lead to to the generation of
larger search spaces. On the other hand, the first difference
presents an obvious place to look for a relative advantage for ZLIFO.
After all, what ZLIFO is doing is delaying separable threats, and Peot
and Smith demonstrated the effectiveness of that approach in their
DSep strategy.
suggest that the use of a
LIFO strategy for unforced flaws should at best make little difference
in search-space size, and may possibly lead to to the generation of
larger search spaces. On the other hand, the first difference
presents an obvious place to look for a relative advantage for ZLIFO.
After all, what ZLIFO is doing is delaying separable threats, and Peot
and Smith demonstrated the effectiveness of that approach in their
DSep strategy.


