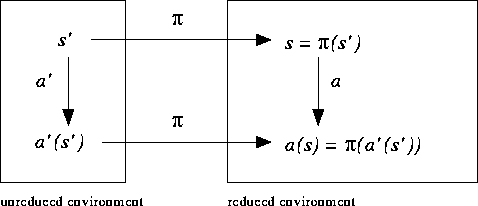
Figure 2: A simple reduction from an environment E' to E. Here s and s' are corresponding states from the reduced and unreduced environments respectively and a and a' are corresponding actions. A projection
Another important kind of structure is when one environment can be considered an abstraction of another [28, 34, 20]. The abstract environment retains the fundamental structure of the concrete environment but removes unimportant distinctions among states. An abstract state corresponds to a set of concrete states and abstract actions correspond to complicated sequences of concrete actions.

Figure 2: A simple reduction from an environment E' to E.
Here s and s' are corresponding states from the reduced and
unreduced environments respectively and a and a' are corresponding
actions. A projection ![]() is a simple reduction if it ``commutes''
with actions, so that
is a simple reduction if it ``commutes''
with actions, so that ![]() , or alternatively,
, or alternatively,
![]() . Thus regardless of whether we take the
projection before or after the action, we will achieve the same
result.
. Thus regardless of whether we take the
projection before or after the action, we will achieve the same
result.
We will say that a projection ![]() from an environment E' to
another environment E is a mapping from the state space of E' to
that of E. We will say that
from an environment E' to
another environment E is a mapping from the state space of E' to
that of E. We will say that ![]() is a simple reduction of
E' to E if for every action a of E, there is a corresponding
action a' of E' such that for any state s'
is a simple reduction of
E' to E if for every action a of E, there is a corresponding
action a' of E' such that for any state s'
![]()
or equivalently, that
![]()
where ![]() is the function composition operator.
We will say that a' is a
is the function composition operator.
We will say that a' is a ![]() -implementation of a and we will use
-implementation of a and we will use
![]() to denote the function mapping E-actions to their
implementations in E'.
to denote the function mapping E-actions to their
implementations in E'.
It is possible to define a much more powerful notion of reduction in which implementations are allowed to be arbitrary policies. It requires a fair amount of additional machinery, however, including the addition of state to the agent. Since simple reduction will suffice for our purposes, we will simply assert the following lemma, which is a direct consequence of the more general reduction lemma [17]: