In general, agents must maintain bindings through some sort of convention, whether it is the structuring of their internal memory, as in the case of a problem solver, or the structuring of their activity. In the case of gaze above, the agent maintains the binding through a convention about the spatial relation between its eye and the object it is binding. All versions of TOAST to date have maintained bindings using conventions about (simulated) spatial arrangement or the states of objects.
One reason TOAST cannot rely solely on gaze binding is that the technique breaks down when binding multiple objects. The agent must continually move its gaze among the objects of interest and so some additional convention must be introduced to ensure that when its gaze leaves the egg and later returns, it always returns to the same egg. (This assumes, of course, that TOAST must return to the same egg. In some tasks it may suffice for TOAST to return to some functionally equivalent egg. If it is preparing three fried eggs and its attention is distracted while preparing to break the second one, it is alright if its attention returns to the third egg, so long as it gets back to the second egg eventually.)
State conventions
The original version of TOAST used the convention eggs were bound to a cooking task iff they were not in their starting (unbroken) state. Eggs were therefore bound using the binding map
which the agent can implement by first visually searching for an unbroken
egg, and then using 
. By corollary 2,
the interleaving of the cooking of multiple eggs can be accomplished by
interleaving the bindings of the eggs. For example, we might assume that
the visual system searched non-deterministically or in a round-robin fashion
for eggs. Any fair interleaving will suffice.
Spatial conventions
Later on in our development of TOAST, we found it useful to adopt the convention that eggs were bound to a cooking task iff they were located in a designated workspace. Cooking eggs are on the counter or in the frying pan, while idle eggs are in the refrigerator. This convention lets the agent use space as an external memory for binding information. To bind the egg, the agent faces the workspace and performs visual search for an egg. Any egg it finds will be an egg being cooked, since idle eggs will be out of view.
This still leaves open the issue of fairness. An extreme but elegant solution to the fairness problem is to use multiple workspaces and employ the convention that each workspace defines a unique binding. To cook two eggs, the agent just works on cooking whatever egg is in front of it, but it spins in place so that it alternates between workspaces.
Formally, the environment then consists of two copies of the workspace and the objects therein plus an extra state component that determines which workspace the agent faces. The agent's perceptual system implements a binding map in which one or the other of the two workspaces is bound depending on the agent's orientation. Given a policy for cooking one egg in one workspace, we can construct a policy for cooking two eggs in two by interleaving the policy with a ``flipping'' operation that switches the workspaces:
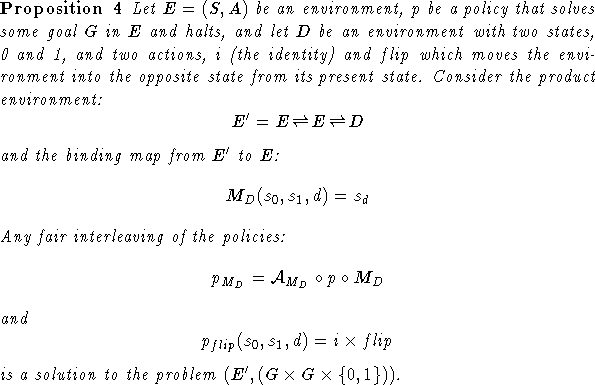
Proof:
Consider the bindings 
and
, and let 
and 
. Since the binding map 
alternates between the bindings 
and 
, any fair
interleaving of 
with 
is equivalent to some
interleaving of 
, 
and . We would
like to show that this interleaving is also fair, that is, that each
of and will get run in finite time. We can
see this from the fact that with each execution of switches
from one binding to another. An objection is that this leaves
open the possibility that that will always get run twice in
a row, thus returning the environment to its original state and so
preventing from switching bindings. This cannot occur, however,
since it would introduce a loop, causing the interleaving to run
forever, never running , and so violating the
assumption of fairness of the interleaving of and
. Thus the interleaving of , and
must be fair. Now note that solves the goal
and halts, solves the goal
and halts, and solves the goal
and halts. Thus by lemma
7, the interleaving solves the intersection of
these goals, which is . 