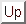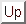

In CNLP and PLINTH, uncertainty is represented through a
combination of uncertain outcomes of nondeterministic actions and the
effects of observing those outcomes. A three-valued logic is used: a
postcondition of an action may be true, false, or
unknown. For example, the action of tossing a coin might have
the postcondition unk(side-up ?x). Special conditional
actions, each of which has an unknown precondition and several
mutually exclusive sets of postconditions, are then used to observe
the results of the nondeterministic actions. In the example, the
operator to observe the results of tossing a coin might have the
precondition unk(side-up ?x) with three possible outcomes:
(side-up heads), (side-up tails), and
(side-up edge).
CNLP thus spreads the representation of uncertainty over both the action whose execution produces the uncertainty and the action that observes the result. A consequence of this is that CNLP cannot use the same observation action to observe the results of different actions. For example, it would require different actions to observe the results of tossing a coin (which has three possible outcomes) and tipping a coin that had landed on its edge (which has two possible outcomes).
In PLINTH, the notion of a conditional action is extended to cover any action (not only observation actions) that has nondeterministic effects on the planner's world model. For example, in an image-processing domain an operator to remove noise from an image may or may not succeed; however, its outcome is evident as soon as it has been applied, and no special observation action is required.
In CNLP and PLINTH, information-gathering actions are included in a plan whenever an action with uncertain effects occurs. This is necessary because the uncertainty is actually represented in the information-gathering action rather than in the action that actually produces the uncertainty. Knowledge goals are thus not represented explicitly in these two systems.
The representation used in CNLP and PLINTH arises out of the desire to use a ``single model of the world, representing the planner's state of knowledge, rather than a more complex formalization including both epistemic and ground formulas'' [Goldman and Boddy 1994b]. An operator therefore represents only the effects that the execution of the underlying action has on the planner's knowledge of the world, and not the effects that it has on the actual state of the world. It is, of course, important to represent how actions affect the planner's world model, but we believe that it is also important to represent how they affect the world. After all, the purpose of reasoning about actions is to achieve goals in the world, not just in the planner's world model. In particular, after the execution of a nondeterministic action its actual effects, although they may indeed be unknown to the planner, have occurred and cannot now be altered. Cassandra's representation reflects this: indeed, Cassandra can reason about the possible effects without scheduling observation actions. This means that an extension of Cassandra can, for example, solve the original bomb-in-the-toilet problem, in which there are no possible actions that will resolve the uncertainty as to which package contains the bomb: the bomb's state is not represented in the planner's world model at any stage between the beginning, when it is known to be armed, and the end, when both packages have been dunked and it is known to be safe.
A further implication of this method of representing uncertainty is the difficulty of representing actions whose uncertain effects cannot be determined through the execution of a single action. Consider, for example, a malfunctioning soda machine that has one indicator that lights when it cannot make change, and another that lights when it has run out of the product requested. Suppose that when it is functioning correctly, these two indicators will not light simultaneously. If it malfunctions, it must be kicked to make it work. Observing either light on its own is not enough to determine which uncertain effect (working properly or malfunctioning) has occurred.