A simple example of these ideas is given by a single bit. In this
case there are two possible classical states 
and 
corresponding to the values 0 and 1, respectively,
for the bit. This defines a two dimensional vector space of
superpositions for a quantum bit. There are a number of proposals for
implementing quantum bits, i.e., devices whose quantum mechanical
properties can be controlled to produce desired superpositions of two
classical values. One example [14, 36] is an atom whose ground state
corresponds to the value 0 and an excited state to the value 1. The use
of lasers of appropriate frequencies can switch such an atom between the
two states or create superpositions of the two classical states. This
ability to manipulate quantum superpositions has been demonstrated in
small cases [56]. Another possibility is
through the use of atomically precise manipulations [14] using a scanning tunneling or atomic
force microscope. This possibility of precise manipulation of chemical
reactions has also been demonstrated [42]. There are also a number of other proposals
under investigation [1, 49, 9], including the
possibility of multiple simultaneous quantum operations [38].
A simple computation on a quantum bit is the logical NOT operation,
i.e., 
and 
. This operator simply exchanges the state vector's
components:
This operation can also be represented as multiplication by the
permutation matrix 
. Another operator is given by the rotation matrix
This can be used to create superpositions from single classical states, e.g.,
This rotation matrix can also be used to illustrate interference,
an important way in which quantum computers differ from probabilistic
classical algorithms. First, consider a classical algorithm with two
methods for generating random bits, 
(producing a ``0'' with probability
) and 
(producing a ``0'' with probability
). Suppose a ``0'' represents a failure
(e.g., a probabilistic search that does not find a solution) while
``1'' represents a success. Finally, let the classical
algorithm consist of selecting one of these methods to use, with
probability p to pick
. Then the overall probability to obtain a
``0'' as the final result is just 
or
The best that can be done is to choose 
, giving a probability of for failure.
A quantum analog of this simple calculation can be obtained from a
rotation with 
. Starting from the individual classical states this
gives superpositions
which correspond to the generators and respectively, because of their respective
probabilities of and to produce a ``0'' when measured. Starting
instead from a superposition of the two classical states,
, corresponds to the step of the classical algorithm
where generator is selected with probability 
. The resulting state after applying the rotation,
, has probability
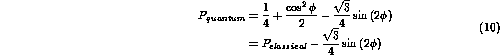
to produce a ``0'' value. In this case the minimum value of
the probability to obtain a ``0'' is not but in fact can be made to equal 0 with the choice
. In this case the amplitudes from the two original
states exactly cancel each other, an example of destructive
interference.
As a final example, illustrating the limits of operations on
superpositions, consider the simple classical program that sets a bit to
the value one. That is, 
and 
. This operation is not reversible: knowing the result
does not determine the original input. By linearity, 
, which in turn is 
. This state violates the normalization condition.
Thus we see that this classical operation is not physically realizable
for a quantum computer. Similarly, another common classical operation,
making a copy of a bit, is also ruled out [51], forming the basis for quantum
cryptography [3].
